北师大版（2024）七年级上册5.3 应用一元一次方程——水箱变高了教案配套课件ppt

这是一份北师大版（2024）七年级上册5.3 应用一元一次方程——水箱变高了教案配套课件ppt，共23页。PPT课件主要包含了学习目标，情境导入，探索交流，单位厘米，解方程得x9，小明的困惑，解得x18，等量关系，长+宽×2周长，x+14等内容，欢迎下载使用。
1.学习建立等量关系，正确列出方程的方法；2.能够解决生活中相关的等积变形和等周长变形问题.
圆柱体的底面半径减小了，高度增大了,体积没变.
常用的体积公式：　　长方体的体积＝长×宽×高；　　正方体的体积＝棱长×棱长×棱长；　　圆柱的体积＝底面积×高＝πr2h．
常用的面积、周长公式：长方形的面积＝长×宽；长方形的周长＝2×（长＋宽）；　正方形的面积＝边长×边长；正方形的周长＝边长×4；
圆的面积＝πr2；圆的周长＝2πr．
如下图，将一个底面直径是20厘米，高为9厘米的“矮胖”形圆柱锻压成底面直径是10厘米的“瘦长”形圆柱，高变成了多少？
锻压前的体积＝锻压后的体积．
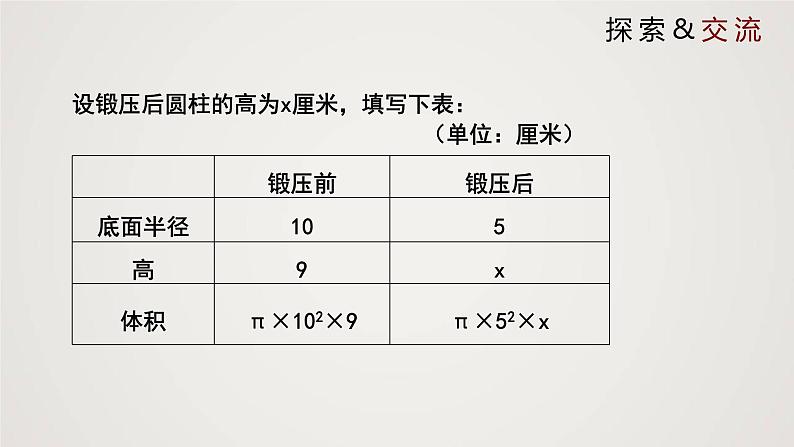
设锻压后圆柱的高为x厘米，填写下表：
根据等量关系，列出方程：
因此，高变成了 厘米
总结：等积变形指图形或物体的形状发生变化，但变化前后的体积或面积不变．等积变形问题中的等量关系是：变化前图形或物体的体积(面积)＝变化后图形或物体的体积(面积)．
例1.小明有一个问题想不明白.他要用一根长为10米的铁线围成一个长方形，使得该长方形的长比宽多1.4米，此时长方形的长、宽各是多少米呢？面积是多少？
解：设长方形的宽为x米，则它的长为 米，根据题意，得：
(x+1.4+x)×2=10
长：1.8+1.4=3.2
此时长方形的长为3.2米，宽为1.8米,面积是5.76平方米.
面积：3.2 × 1.8=5.76
例2.小明又想用这10米长铁线围成一个长方形.（1）使长方形的长比宽多0.8米，此时长方形的长、宽各为多少米？它所围成的长方形与第一次所围成的长方形相比，面积有什么变化？
解：（1）设长方形的宽为x米，则它的长为（x+0.8）米.根据题意，得：
(x+0.8 +x)×2=10
长：2.1+0.8=2.9
面积：2.9×2.1=6.09(米2)
此时长方形的长为2.9米，宽为2.1米，面积为6.09平方米.此时长方形的面积比第一次围成的面积增大6.09-5.76=0.33(平方米).
（2）若使长方形的长和宽相等，即围成一个正方形，此时正方形的边长是多少米？围成的面积与第二次围成的面积相比，又有什么变化？
(x +x) ×2 =10
面积：2.5×2.5=6.25(米2)
解：（2）设正方形的边长为x米.根据题意，得：
面积增大：6.25-6.09=0.16（平方米）
此时正方形边长为2.5米，面积为6.25平方米.比第二次的面积增大0.16平方米.
同样长的铁丝围成怎样的四边形面积最大呢？
面积：1.8×3.2=5.76
面积;2.9×2.1=6.09
面积：2.5×2.5=6.25
列方程解应用题的一般步骤：设未知数、列方程、解方程、检验所得结果、确定答案；可简要地概括为“设、列、解、检、答”．
例3.3月12日是植树节，七年级170名学生参加义务植树活动，如果平均一名男生一天能挖树坑3个，平均一名女生一天能种树7棵，要正好使每个树坑种一棵树，则该年级的男生、女生各有多少人？ (1)审题：审清题意，找出已知量和未知量；
(2)设未知数：设该年级的男生有x人，那么女生有_____ 人；(3)列方程：根据相等关系，列方程为_____________；(4)解方程，得x＝______，则女生有 人；(5)检验：将解得的未知数的值放入实际问题中进行验证；(6)作答：答：该年级有男生____人，女生____人．
3x=7(170 － x)
1.欲将一个长、宽、高分别为150mm、150mm、20mm的长方体钢毛坯，锻造成一个直径为100 mm的钢圆柱体，则圆柱体的高是(　　)A．1200mm B. mmC．120πmm D．120mm
2.用一根长60厘米的铁丝围成一个长方形． 使长方形的宽是长 的 ，求这个长方形的长、宽．(按长、宽的顺序填写)
3.如图，有甲、乙两个容器，甲容器盛满水，乙容器里没有水，现将甲容器中的水全部倒入乙容器，问：乙容器中的水会不会溢出？如果不会溢出，请你求出倒入水后乙容器中的水深；如果水会溢出，请你说明理由．(容器壁厚度忽略不计，图中数据的单位：cm)