初中数学北师大版（2024）七年级下册3 平行线的性质评课ppt课件

这是一份初中数学北师大版（2024）七年级下册3 平行线的性质评课ppt课件，共29页。PPT课件主要包含了学习目标，两直线平行，同位角，内错角，同旁内角，平行线的性质总结，平行线的性质等内容，欢迎下载使用。
1 经历测量、交流、思考等活动归纳并掌握平行线的性质，并能解决一些问题。2 经历观察、操作、想象、推理、交流等活动，进一步发展空间观念、推理能力和有条理表达的能力。
关于平行线的判定你还记得吗？
判定方法 1 同位角相等，两直线平行. 判定方法 2 内错角相等，两直线平行.判定方法 3 同旁内角互补，两直线平行.
两条平行线被第三条直线所截
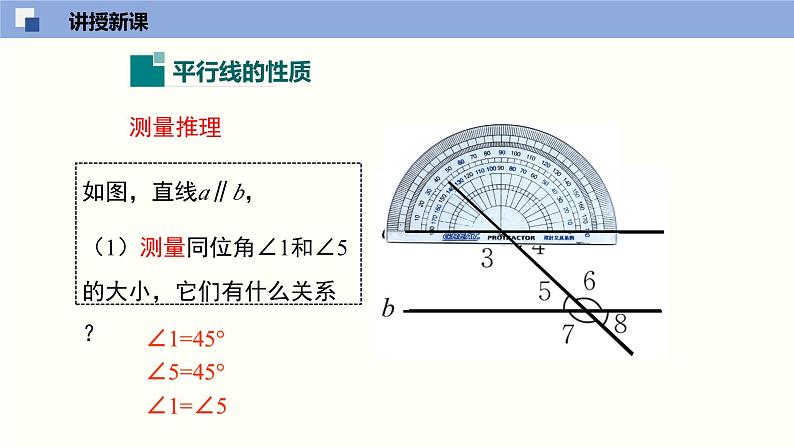
如图，直线a∥b，（1）测量同位角∠1和∠5的大小，它们有什么关系？
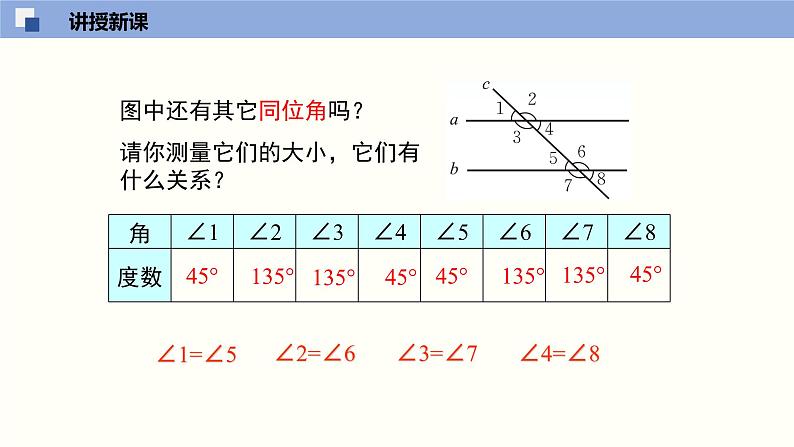
图中还有其它同位角吗？请你测量它们的大小，它们有什么关系？
让我们换一个图形试试呢？请你测量各角的大小，其中同位角有什么关系？
一般地，平行线具有性质：
性质1：两条平行线被第三条直线所截，同位角相等.简单说成：两直线平行，同位角相等.
∴∠1=∠2 （两直线平行，同位角相等）
例： 如图，若AB∥CD，且∠1＝∠2，试判断AM 与CN的位置关系，并说明理由．解析：AM与CN的位置关系很显然 是平行，要说明AM∥CN， 可考虑说明∠EAM＝∠ECN. 因为∠1＝∠2， 所以只需说明∠BAE＝∠ACD即可，由于“两 直线平行，同位角相等”，所以根据 AB∥CD 即可得出∠BAE＝∠ACD.
解：AM∥CN. 理由：∵AB∥CD(已知)， ∴∠BAE＝∠ACD(两直线平行，同位角相等)． 又∵∠1＝∠2(已知)， ∴∠EAM＝∠ECN(等式性质)． ∴AM∥CN(同位角相等，两直线平行)．
如图，直线a∥b，（2）图中有几对内错角？它们的大小有什么关系？为什么？
证明：∵ a∥b （已知）
∴∠1＝∠5（两直线平行，同位角相等）　　　　　　　　
又∵∠1=∠4（对顶角相等）
∴ ∠4=∠5（等量代换）
2对内错角∠4=∠5=45°∠3=∠6=135°
性质2：两条平行线被第三条直线所截，内错角相等.简单说成：两直线平行，内错角相等.
∴∠2=∠3 （两直线平行，内错角相等）
例 如图，已知直线a∥b，∠1 = 50°, 求∠2的度数.
所以∠ 2= 50° (等量代换).
解：因为 a∥b(已知),
所以∠ 1= ∠ 2(两直线平行,内错角相等).
又因为∠ 1 = 50° (已知),
如图，直线a∥b，（3）图中有几对同旁内角？它们的大小有什么关系？为什么？
2对同旁内角∠3+∠5=180°∠4+∠6=180°
又∵∠1+∠3=180°（邻补角定义）
∴ ∠3+∠5=180°（等量代换）
性质3：两条平行线被第三条直线所截，同旁内角互补.简单说成：两直线平行，同旁内角互补.
∵a∥b（已知）∴∠2+∠4=180 °（两直线平行，内错角相等）
例 如图是一块梯形铁片的残余部分，量得∠A=100°，∠B=115°，梯形的另外两个角的度数分别是多少？
解：因为梯形上、下底互相平行，所以∠A与∠D互补， ∠B与∠C互补.
所以梯形的另外两个角分别是80°,65°.
于是∠D=180 °-∠A=180°-100°=80°,∠C= 180 °-∠B=180°-115°=65°.
角的关系（相等或互补）
1.如图，已知a∥b，小华把三角板的直角顶点放在直线b上．若∠1＝40°，则∠2的度数为(　　)A．100° B．110° C．120° D．130°
2.已知直线m∥n，将一块含30°角的直角三角尺ABC按如图方式放置(∠ABC＝30°)，其中A，B两点分别落在m，n上，若∠1＝20°，则∠2的度数为(　　)A．20° B．30° C．45° D．50°
3.如图，已知AB∥CD∥EF，FC平分∠AFE，∠C＝25°，则∠A的度数是(　　)A．25° B．35° C．45° D．50°
4.如图所示，要在一条公路的两侧铺设平行管道，已知一侧铺设的角度为120°，为使管道对接，另一侧铺设的角度大小应为(　　)A．120° B．100° C．80° D．60°
5.如图，BCD是一条直线，∠A＝75°，∠1＝53°，∠2＝75°，求∠B的度数．
解： ∵ ∠A＝∠2＝75°，∴AB∥CE．（同位角相等，两直线平行）∴∠B＝∠1＝53°．（两直线平行，内错角相等）
6.如图 ，一束平行光线AB与DE射向一个水平镜面后被反射，此时∠1=∠2，∠3=∠4．（1）∠1与∠3的大小有什么关系？∠2与∠4呢？（2）反射光线BC与EF也平行吗？
解：（1）由 AB∥DE，可以得到∠1＝∠3，由∠1＝∠2， ∠3＝∠4，可以得到∠2＝∠4；（2）由∠2＝∠ 4，可以得到BC∥EF.
7. 如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
解:∵EF∥AD,∴∠1=∠BAD.又∵∠1=∠2,∴∠2=∠BAD,∴AB∥DG,∴∠BAC+∠AGD=180°.∵∠BAC=70°,∴∠AGD=110°.
两直线平行同旁内角互补