初中数学北师大版（2024）七年级下册1 认识三角形备课课件ppt

这是一份初中数学北师大版（2024）七年级下册1 认识三角形备课课件ppt，共31页。PPT课件主要包含了学习目标，导入新课，讲授新课，cab，顶点C，顶点A，顶点B，△ABE，方法一，方法二等内容，欢迎下载使用。
1.认识三角形；2.理解三角形内角和定理的内容，能应用三角形内角和定理解决一些简单的实际问题；3.掌握三角形的分类，能用有两个角互余的三角形是直角三角形对三角形进行判定．
下面请同学们仔细观察一组图片，找出你熟悉的三角形
观察下面的屋顶框架图（1）你能从图中找出几个不同的三角形吗？（2）这些三角形有什么共同的特点？
【解析】（1）7个（2）三个顶点、三个角、三条边构成
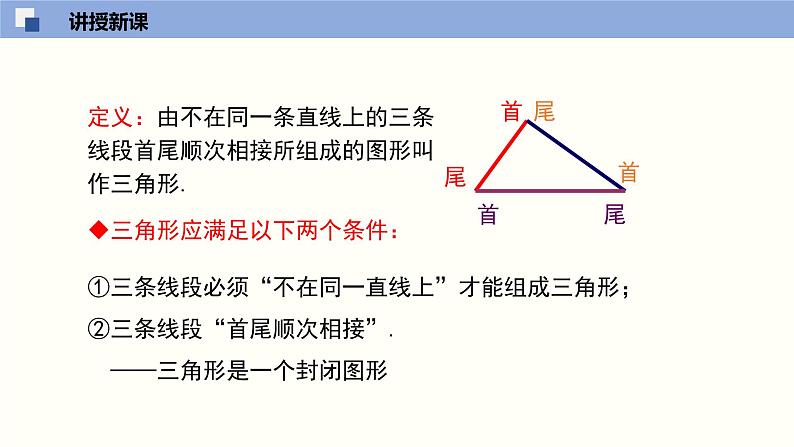
定义：由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形.
三角形应满足以下两个条件：
①三条线段必须“不在同一直线上”才能组成三角形；②三条线段“首尾顺次相接”. ——三角形是一个封闭图形
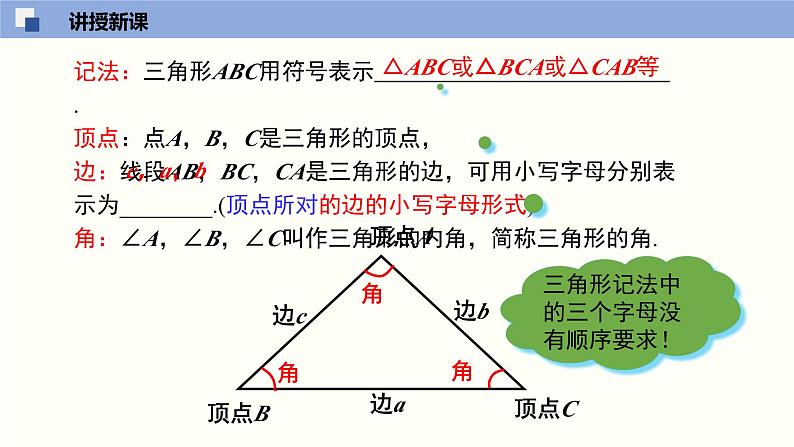
记法：三角形ABC用符号表示 .顶点：点A，B，C是三角形的顶点，边：线段AB，BC，CA是三角形的边，可用小写字母分别表示为________.(顶点所对的边的小写字母形式)角：∠A，∠B，∠C叫作三角形的内角，简称三角形的角.
△ABC或△BCA或△CAB等
三角形记法中的三个字母没有顺序要求！
例1 找一找（1）图中有几个三角形？用符号表示出这些三角形？
（2）以AB为边的三角形有哪些？
（3）以E为顶点的三角形有哪些？
5个，分别是△ABE,△ABC,△BEC,△BCD,△ECD.
△ ABE 、△BCE、 △CDE.
（4）以∠D为角的三角形有哪些？
△ BCD、 △DEC.
（5）说出△BCD的三个角和三个顶点所对的边.
△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC，顶点C所对应的边为BD，顶点D所对应的边为BC.
我们知道，将一个三角形的内角撕下来，拼在一起，可以得到三角形的内角和为180°，你知道如何拼接以及说明的依据是什么吗？
还有其他的拼接方法吗？可否在边上任意一点处拼接呢？
原理就是把分散的三个角聚集在一起成为平角
证法1：延长BC到D，过点C作CE∥BA，∴ ∠A=∠1 .(两直线平行，内错角相等) ∠B=∠2.(两直线平行，同位角相等)又∵∠1+∠2+∠ACB=180°(平角定义)， ∴∠A+∠B+∠ACB=180°(等量代换).
证法2：过点A作l∥BC， ∴∠B=∠1.(两直线平行,内错角相等) ∠C=∠2.(两直线平行,内错角相等) ∵∠2+∠1+∠BAC=180°(平角定义)，∴∠B+∠C+∠BAC=180°(等量代换).
证法3：过D作DE∥AC,作DF∥AB.∴ ∠C=∠EDB,∠B=∠FDC.(两直线平行，同位角相等) ∠A+∠AED=180°,∠AED+∠EDF=180°，(两直线平行，同旁内角相补)∴ ∠A=∠EDF.∵∠EDB+∠EDF+∠FDC=180°(平角定义)，∴∠A+∠B+∠C=180°(等量代换).
思考：多种方法证明三角形内角和等于180°的核心是什么？
借助平行线的“移角”的功能，将三个角转化成一个平角.
例2 已知，如图，D是△ABC中BC边延长线上一点，F为AB上一点，直线FD交AC于E，∠DFB＝90°，∠A＝46°，∠D＝50°.求∠ACB的度数．
解：在△DFB中，∵∠DFB＝90°，∠D＝50°，∠DFB＋∠D＋∠B＝180°，∴∠B＝40°.在△ABC中，∵∠A＝46°，∠B＝40°，∴∠ACB＝180°－∠A－∠B＝94°.
如下图，有三个三角形，它们的两个内角被挡住了，你能判断出被挡住的角是什么角吗？
锐角三角形（三个锐角）
直角三角形（一个直角、两个锐角）
钝角三角形（一个钝角、两个锐角）
我们可以按三角形内角的大小把三角形分为三类：
根据“三角形的内角和为180°”易得“直角三角形的两个锐角互余”.
1. 常用符号“Rt△ABC”来表示“直角三角形ABC” 把直角所对的边称为直角三角形的斜边; 夹直角的两条边称为直角边. 2. 直角三角形的两个锐角之间有什么关系？ 直角三角形的两个锐角互余
例3 在△ABC中，∠A∶∠B∶∠C＝1∶2∶3，试判断△ABC的形状，并说明理由．
解：△ABC是直角三角形．理由如下：∵∠A∶∠B∶∠C＝1∶2∶3，∴可设∠A，∠B，∠C的度数分别为x°，2x°，3x°.∵∠A＋∠B＋∠C＝180°，∴x°＋2x°＋3x°＝180°，解得x°＝30°.∴∠A＝30°，∠B＝60°，∠C＝90°.∴△ABC是直角三角形．
1. 下图是小明同学用三根木棒拼成的图形,其中是三角形的是(　　)
2. 一副三角尺如图摆放(直角顶点C重合),边AB与CE交于点F,DE//BC,则∠BFC的度数为(　　)A.105° B.100° C.75° D.60°
3. 在△ABC中,若一个内角等于另外两个内角的差,则这个三角形是(　　)A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
4. 如图，以CD为公共边的三角形是_______________；∠EFB是________的内角；在△BCE中，BE所对的角是________，∠CBE所对的边是__________；以∠A为公共角的三角形_______________________．
△ABD，△ACE和△ABC
5.（1）在△ABC中,∠A=35°,∠ B=43°， 则∠ C =_______;
（2）在△ABC中,∠A:∠B:∠C=1:1:4, 则∠A = _______;
（3）在△ABC中, ∠A=40°,∠A=2∠B， 则∠C = ________.
6.在△ABC中，∠A的度数是∠B的度数的3倍，∠C 比∠B 大15°，求∠A，∠B，∠C的度数并说明三角形的形状.
解：设∠B为x °，则∠A为(3x)°，∠C为(x+ 15)°.
3x+x+(x+15)=180，解得 x=33.
所以 3x=99 ，x+15 =48.
即∠A,∠B,∠C的度数分别为99°>90°，33°，48°，所以三角形是钝角三角形.
根据三角形的内角和等于180°， 得
7. 一个零件的形状如图,按规定∠A=90°,∠ABD和∠ACD应分别是32°和21°.检验工人量得∠BDC=148°,就断定这个零件不合格.请你运用三角形的有关知识说明零件不合格的理由.
解:如图,连接BC.因为∠A=90°,若零件合格,则∠ACB+∠ABC=90°. 而∠1+∠2=180°-148°=32°,∠ACB+∠ABC=∠ACD+∠ABD+∠1+∠2=21°+32°+32°=85°≠90°,故这个零件不合格.
三角形的概念：由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.
三角形的内角和等于180°
直角三角形的两个锐角互余