初中数学第四章 三角形3 探索三角形全等的条件说课课件ppt

这是一份初中数学第四章 三角形3 探索三角形全等的条件说课课件ppt，共30页。PPT课件主要包含了学习目标，两个角，一条边，边边边SSS，“两角及夹边”，“角边角”判定方法，几何语言，∠C＝∠F，∠B＝∠E，BC＝EF等内容，欢迎下载使用。
1．经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程；2．掌握三角形的“角边角”、“角角边”条件，以及它们的符号语言；3、会用“ASA”、“AAS”判定两个三角形全等。
小明用板挡住了两位同学所画的两个三角形，你能画出这两个三角形吗？
发现： 和 可以确定一个三角形。
1.什么叫全等三角形？
能够完全重合的两个三角形叫 全等三角形.
2. 我们已经学过了哪几种判定两个三角形全等的方法？
3.如果已知一个三角形的两角及一边，那么有几种可能的情况呢？
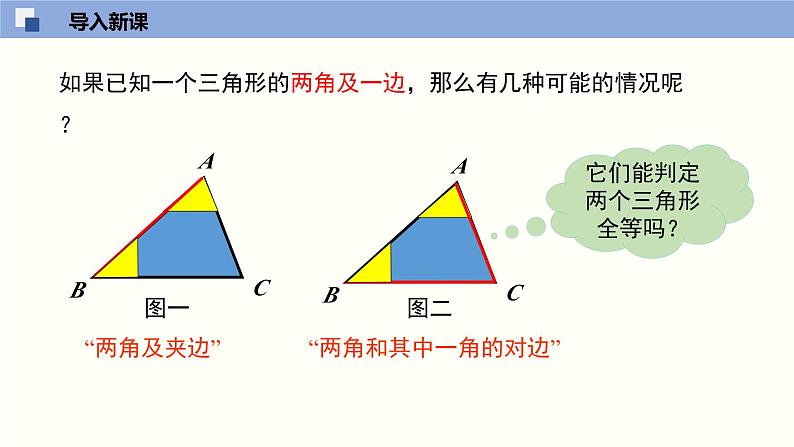
如果已知一个三角形的两角及一边，那么有几种可能的情况呢？
“两角和其中一角的对边”
它们能判定两个三角形全等吗？
探究一：任意画出一个△ABC，再画一个△A′B′C′，使A′B′＝AB，∠A′＝∠A，∠B′＝∠B（即保证两角和它们的夹边对应相等）．把画好的△A′B′C′剪下，放到△ABC上，它们全等吗？
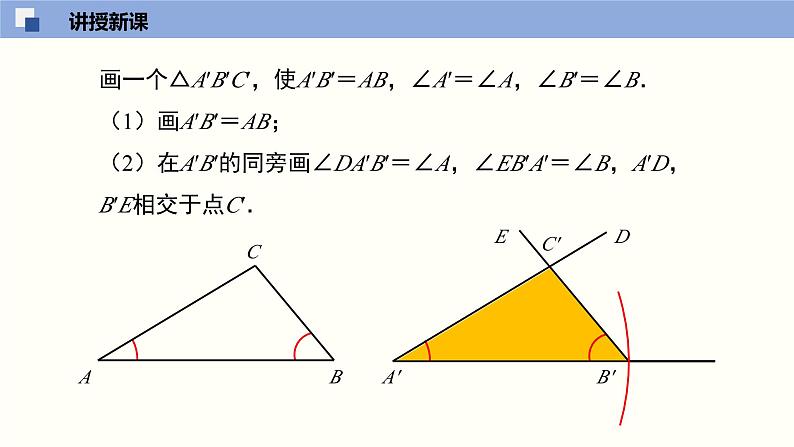
画一个△A′B′C′，使A′B′＝AB，∠A′＝∠A，∠B′＝∠B．（1）画A′B′＝AB；（2）在A′B′的同旁画∠DA′B′＝∠A，∠EB′A′＝∠B，A′D，B′E相交于点C′．
两角和它们的夹边分别相等的两个三角形全等（可以简写成“角边角”或“ASA”）.
在△ABC和△DEF中，
∴△ABC≌△DEF（ASA）．
例1 如图，已知AB＝AE，∠1＝∠2，∠B＝∠E.试说明：BC＝ED.
解：∵∠1＝∠2，∴∠1＋∠BAD＝∠2＋∠BAD，即∠BAC＝∠EAD.在△BAC和△EAD中，∴△BAC≌△EAD(ASA)．∴BC＝ED.
∠B=∠E（已知 ）， AB=AE（已知），∠BAC=∠EAD （已证 ），
找相等角的方法：1.公共角、对顶角分别相等；2.等角加(减)等角，其和(差)相等；3.同角或等角的余(补)角相等；4.角平分线得到相等角；5.平行线的同位角、内错角相等；6.直角都相等；7.全等三角形对应角相等.
探究二：在两个三角形中，是不是只要有两个角对应相等，一条边对应相等，这两个三角形就全等呢？下面，我们来看一个问题：如图，在△ABC和△DEF中，∠A＝∠D，∠B＝∠E，BC＝EF．求证：△ABC≌△DEF．
证明：在△ABC中，∠A＋∠B＋∠C＝180°，∴∠C＝180°－∠A－∠B．同理∠F＝180°－∠D－∠E．又∠A＝∠D，∠B＝∠E，∴∠C＝∠F．在△ABC和△DEF中
∠B＝∠E,BC＝EF,∠C＝∠F,
两角和其中一角的对边分别相等的两个三角形全等（可以简写成“角角边”或“AAS”）．
∴△ABC≌△DEF（AAS）．
例2 如图，已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E.试说明：△BDA≌△AEC；
解：(1)∵BD⊥m，CE⊥m，∴∠ADB＝∠CEA＝90°，∴∠ABD＋∠BAD＝90°.∵AB⊥AC，∴∠BAD＋∠CAE＝90°，∠ABD＝∠CAE.在△BDA和△AEC中，
∠ADB=∠CEA=90°， ∠ABD＝∠CAE,AB＝AC，
∴△BDA≌△AEC(AAS).
已知：如图，△ABC ≌△A′B′C′ ，AD和A′ D′ ，AE和A'E'分别是△ABC 和△A′B′C′的高和角平分线.试说明AD＝ A′D′ ，AE＝ A′E′ ，并用一句话说出你的发现.
1. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1，2，3，4的四块)，你认为将其中的哪块带去，就能配一块与原来一样大小的三角形玻璃？应该带(　　)A．第1块 B．第2块 C．第3块 D．第4块
2. 如图，点B，F，C，E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是(　　)A．AB＝DE B．AC＝DFC．∠A＝∠D D．BF＝EC
3. 如图，AB∥CD，且AB＝CD，AC与BD相交于点E，则△ABE≌△CDE的根据是(　　)A．只能用ASA B．只能用SSSC．只能用AAS D．用ASA或AAS
4.下列结论中，正确的是（ 　 ）A．有两条边对应相等的两个三角形全等B．有一个角和两条边对应相等的两个三角形全等C．有两个角和它们的夹边对应相等的两个三角形全等D．任意两个直角三角形全等
5. 如图所示,已知∠B=∠D,∠C=∠E,AC=AE,则AB与AD相等吗?小强同学的思考过程如下,试在括号里填写相应的理由.
在△ABC与△ADE中,因为∠B=∠D,∠C=∠E,AC=AE(　　　), 所以△ABC≌△ADE(　　 ), 所以AB=AD(　　　　　　　　 　　).
全等三角形的对应边相等
6. 已知：如图，点B，F，C，E在一条直线上，∠A＝∠D，AC＝DF，且AC∥DF.试说明：△ABC≌△DEF.
证明：因为AC∥DF，所以∠ACB＝∠DFE.又因为∠A＝∠D，AC＝DF，所以△ABC≌△DEF(ASA)．
7. 我们把两组邻边相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AB＝CB，AD＝CD.对角线AC，BD相交于点O，OE⊥AB，OF⊥CB，垂足分别是E，F.试说明：OE＝OF.
证明：因为在△ABD和△CBD中，所以△ABD≌△CBD(SSS)．所以∠ABD＝∠CBD.又因为OE⊥AB，OF⊥CB，所以∠OEB＝∠OFB.在△BOE和△BOF中，所以△BOE≌△BOF(AAS)．所以OE＝OF.
8.如图，在△ABC中，AD＝BD，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点H，则BH与AC相等吗？为什么？解：∵AD⊥BC，∴∠ADB＝∠ADC＝90°．∴∠CAD＋∠C＝90°．∵BE⊥AC，∴∠BEC＝90°．∴∠CBE＋∠C＝90°．∴∠CBE＝∠CAD．在△BDH和△ADC中，∴△BDH≌△ADC（ASA）．∴BH＝AC．
9．如图，点D在AB上，点E在AC上，BE和CD相交于点O，AB＝AC，∠B＝∠C．求证：BO＝CO．
证明：在△ACD和△ABE中，
∴△ACD≌△ABE（ASA）．
∴AB－AD＝AC－AE．即BD＝CE．
在△BOD和△COE中，
∴△BOD≌△COE（AAS）．
三角形全等的“ASA”判定：两角及其夹边分别相等的两个三角形全等.
三角形全等的“AAS”判定：两角分别相等且其中一组等角的对边相等的两个三角形全等.
注意两角与边位置关系的区别