初中3.2 实数获奖ppt课件

这是一份初中3.2 实数获奖ppt课件，文件包含32从有理数到实数pptx、核心素养教学设计docx、核心素养导学案docx等3份课件配套教学资源，其中PPT共45页， 欢迎下载使用。
1.了解无理数和实数的概念与分类，知道实数由有理数和无理数组成；2.了解实数与数轴上的点一一对应，能用数轴上的点表示实数；3.能用有理数估计一个无理数的大致范围；4.了解实数的比较大小。
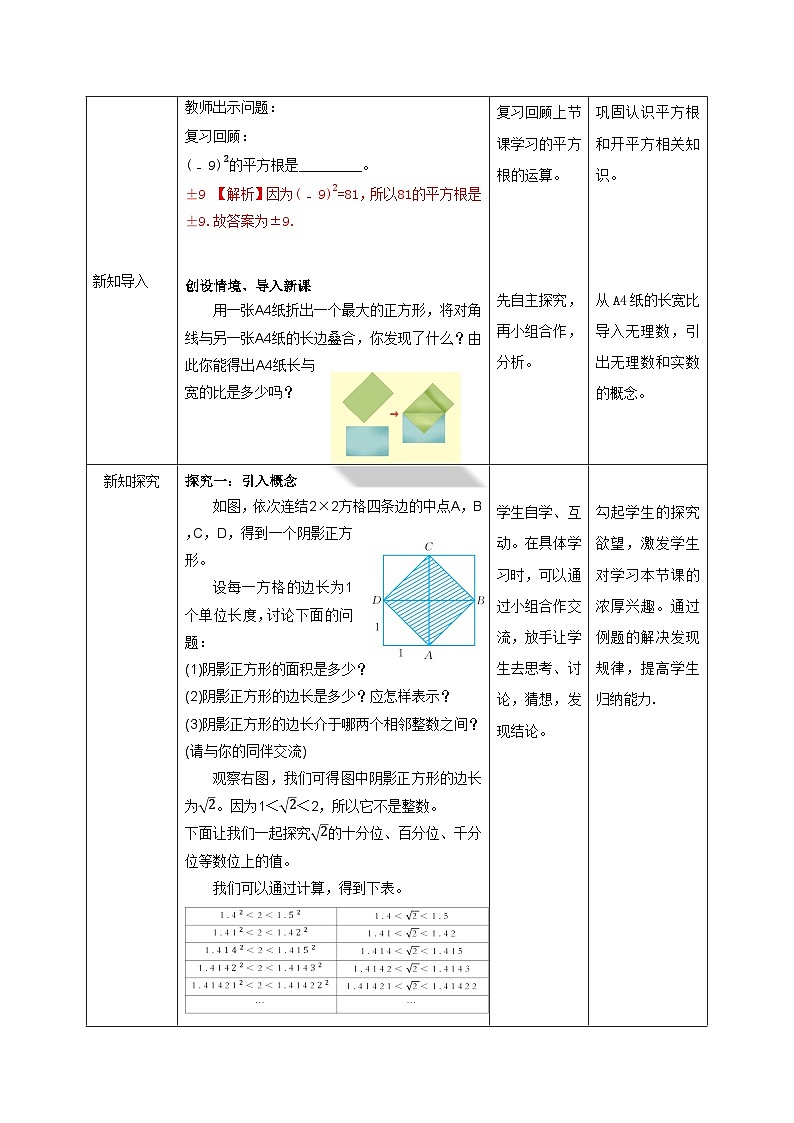
如图，依次连结2×2方格四条边的中点A，B，C，D，得到一个阴影正方形。设每一方格的边长为1个单位长度，讨论下面的问题：(1)阴影正方形的面积是多少？(2)阴影正方形的边长是多少？应怎样表示？(3)阴影正方形的边长介于哪两个相邻整数之间？(请与你的同伴交流)
我们可以通过计算，得到下表。
按正实数，零，负实数的关系分类：
注意对实数进行分类时，可以有不同的方法，但要按统一标准，做到不重不漏.
-3 -2 -1 0 1 2
-2 -1 0 1 2
在实数范围内，每一个实数都可以用数轴上的点来表示；反过来，数轴上的每一个点都表示一个实数。我们说实数和数轴上的点一一对应。有理数的大小比较法则也适用于实数。在数轴上表示的两个实数，右边的数总比左边的数大。
拓展(1)实数与数轴上的点是一一对应的，而与有理数就不是一一对应的，实数包括有理数.(2)数轴上的任意一点表示的数，不是有理数，就是无理数.
-3 -2 -1 0 1 2 3
利用估算法确定无理数的大小对于带根号的无理数的大小的估算，可以通过平方运算或立方运算，采用两边逐渐逼近的方法，首先确定其整数部分，再确定十分位、百分位等小数部分。
负实数 正实数
实数的大小比较1.利用数轴比较实数的大小与有理数的大小比较法则一样，在数轴上表示的两个实数，右边的数总比左边的数大.2.利用实数的分类比较大小(1)正实数大于零，负实数小于零，正实数大于负实数.(2)两个正实数，绝对值大的数较大.(3)两个负实数，绝对值大的数反而小
-3 -2 -1 0 1 2 3
M N P Q
O A C B
【必做】1.有下列说法：(1)无理数就是开方开不尽的数；(2)无理数是无限不循环小数；(3)无理数包括正无理数、零、负无理数；(4)一个无理数的平方一定是有理数.其中正确的说法的个数是A.1 B.2 C.3 D.4
A【解析】(1)π是无理数，但不是开方开不尽的数，故原说法错误；(2)无理数就是无限不循环小数，故原说法正确；(3)0是有理数，不是无理数，故原说法错误；(4)π是无理数，故原说法错误，故选A.
【必做】3.如图，数轴上的两点A,B对应的实数分别是a，b，则下列式子中成立的是A.1-2a>1-2bB.-a