湖北省武汉市华宜寄宿学校2024-2025学年八年级上学期10月月考数学试题(无答案)(01)

这是一份湖北省武汉市华宜寄宿学校2024-2025学年八年级上学期10月月考数学试题(无答案)(01)，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

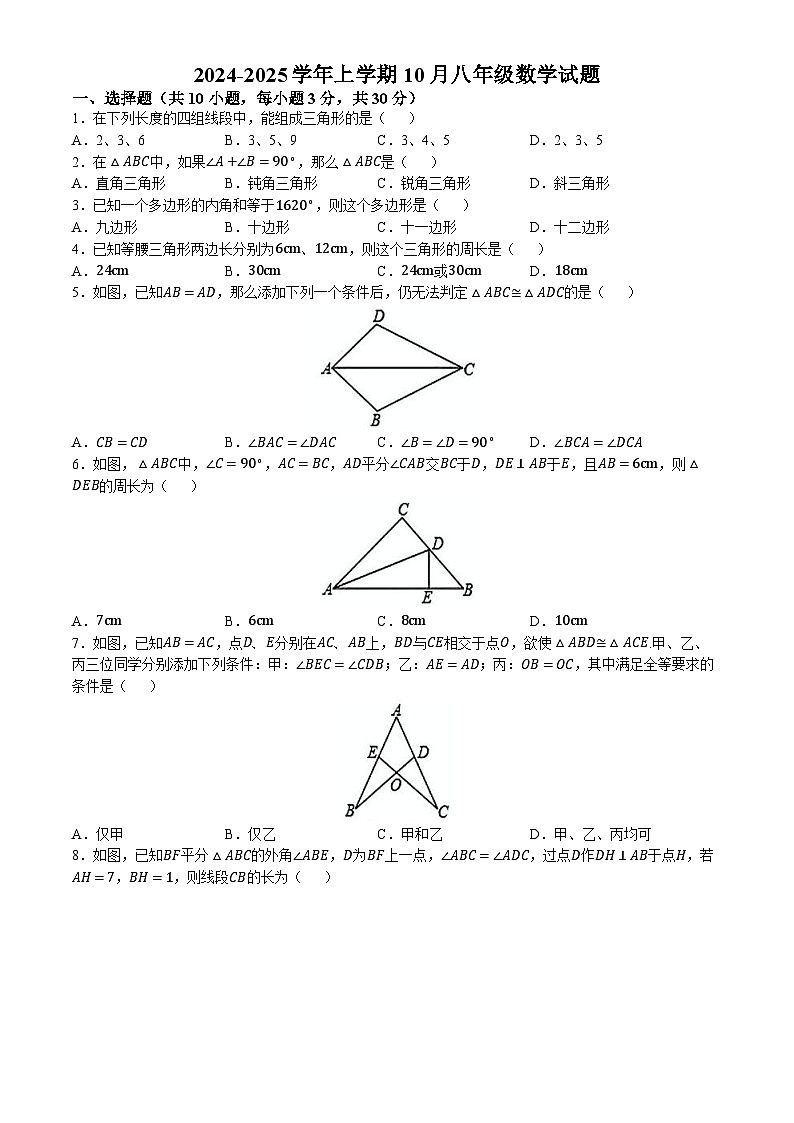
1．在下列长度的四组线段中，能组成三角形的是（ ）
A．2、3、6B．3、5、9C．3、4、5D．2、3、5
2．在△ABC中，如果∠A+∠B=90​∘，那么△ABC是（ ）
A．直角三角形B．钝角三角形C．锐角三角形D．斜三角形
3．已知一个多边形的内角和等于1620​∘，则这个多边形是（ ）
A．九边形B．十边形C．十一边形D．十二边形
4．已知等腰三角形两边长分别为6cm、12cm，则这个三角形的周长是（ ）
A．24cmB．30cmC．24cm或30cmD．18cm
5．如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≅△ADC的是（ ）
A．CB=CDB．∠BAC=∠DACC．∠B=∠D=90​∘D．∠BCA=∠DCA
6．如图，△ABC中，∠C=90​∘，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB=6cm，则△DEB的周长为（ ）
A．7cmB．6cmC．8cmD．10cm
7．如图，已知AB=AC，点D、E分别在AC、AB上，BD与CE相交于点O，欲使△ABD≅△ACE.甲、乙、丙三位同学分别添加下列条件：甲：∠BEC=∠CDB；乙：AE=AD；丙：OB=OC，其中满足全等要求的条件是（ ）
A．仅甲B．仅乙C．甲和乙D．甲、乙、丙均可
8．如图，已知BF平分△ABC的外角∠ABE，D为BF上一点，∠ABC=∠ADC，过点D作DH⊥AB于点H，若AH=7，BH=1，则线段CB的长为（ ）
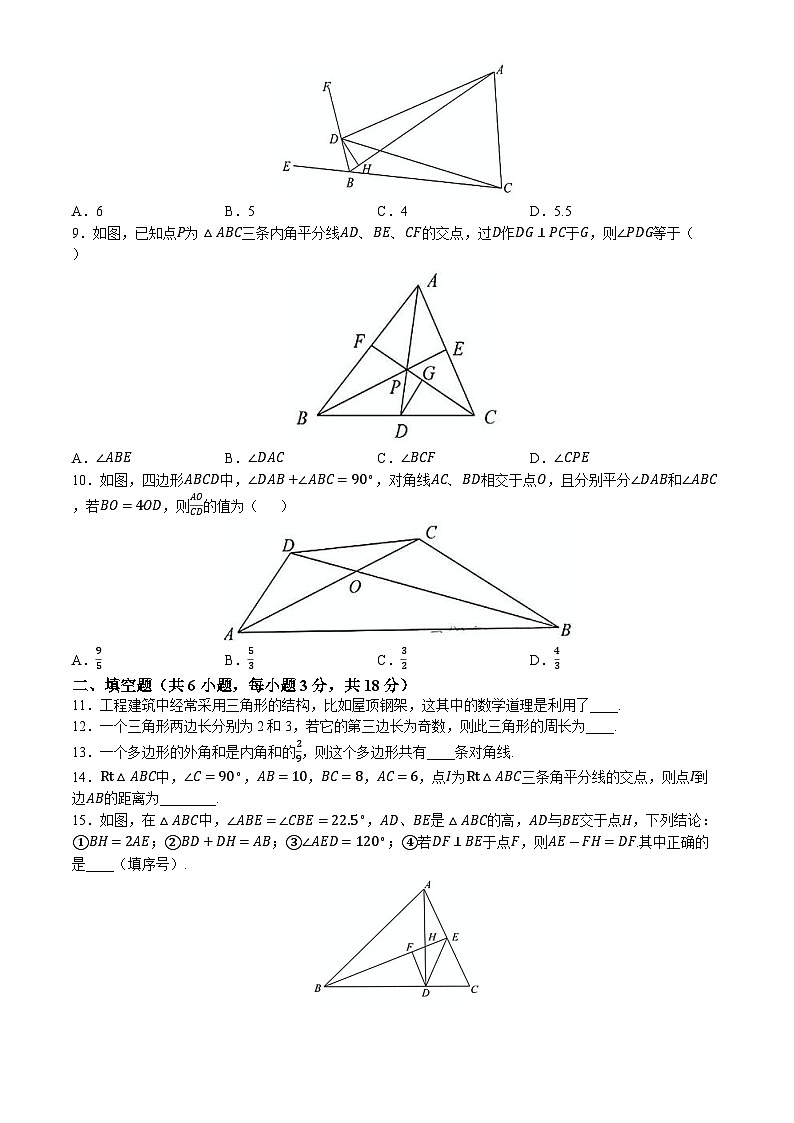
A．6B．5C．4D．5.5
9．如图，已知点P为△ABC三条内角平分线AD、BE、CF的交点，过D作DG⊥PC于G，则∠PDG等于（ ）
A．∠ABEB．∠DACC．∠BCFD．∠CPE
10．如图，四边形ABCD中，∠DAB+∠ABC=90​∘，对角线AC、BD相交于点O，且分别平分∠DAB和∠ABC，若BO=4OD，则AOCD的值为（ ）
A．95B．53C．32D．43
二、填空题（共6小题，每小题3分，共18分）
11．工程建筑中经常采用三角形的结构，比如屋顶钢架，这其中的数学道理是利用了____.
12．一个三角形两边长分别为2和3，若它的第三边长为奇数，则此三角形的周长为____.
13．一个多边形的外角和是内角和的29，则这个多边形共有____条对角线.
14．Rt△ABC中，∠C=90​∘，AB=10，BC=8，AC=6，点I为Rt△ABC三条角平分线的交点，则点I到边AB的距离为________.
15．如图，在△ABC中，∠ABE=∠CBE=22.5​∘，AD、BE是△ABC的高，AD与BE交于点H，下列结论：①BH=2AE；②BD+DH=AB；③∠AED=120​∘；④若DF⊥BE于点F，则AE-FH=DF.其中正确的是____（填序号）.
16．如图，△ABC中，AB-AC=4，BC=7，BD垂直于∠BAC的角平分线AD于点D，E为AC的中点，连接BE交AD于F，则△BDF、△AEF的面积之差的最大值为______.
三、解答题（共8题，共72分）
17．（本题8分）在△ABC中，若∠A=2∠B=2∠C，请判断这个三角形的形状，并说明理由.
18．（本题8分）如图，点B、E、C、F在一条直线上，AB//DE，∠A=∠D，BE=CF，求证：AC//DF.
19．（本题8分）如图，A、C、E三点在同一条直线上，AB=AD，∠B=∠DAC，BC=AE.
（1）求证：BC=DE+CE；
（2）当△ABC满足__________时，BC//DE？
20．（本题8分）如图1，在△ABC中，两个内角∠ABC和∠ACB的平分线交于点O，连接AO，OE⊥AB于点E，OF⊥AC于点F.
（1）求证：AO平分∠BAC；
（2）如图2，延长CA至点D，使CD=CB，若∠D=∠AOD，∠ACB=66​∘，求∠BAC的度数.
21．（本题8分）如图1，在14×7的长方形网格中，每个小正方形的边长为1，小正方形的每一个顶点叫做格点.线段ED和△ABC的顶点都在格点上.
（1）直接写出S△ABC=______.
（2）请仅用无刻度直尺完成下列画图，不写画法，保留画图痕迹.
①请画出△ABC的中线AP和高BH.
②在线段ED右侧找到点F，使得△ABC≅△EFD.
（3）要求在图2中仅用无刻度的直尺作图在x轴上找点F，使AE平分∠BEF.
22．（本题10分）如图，△ABC中，CD⊥AB于点D，CD=BD，点E在CD上，DE=DA，连接BE.
（1）求证：BE=CA；
（2）延长BE交AC于点F，连接DF，求∠CFD的度数；
（3）过点C作CM⊥CA，CM=CA，连接BM交CD于点N，若BD=12，AD=5，直接写出△NBC的面积______.
23．（本题10分）如图1，在五边形ABCDE中，∠E=90​∘，BC=DE，连接AC、AD，且AB=AD，AC⊥BC.
（1）求证：AC=AE；
（2）如图2，若∠ABC=∠CAD，AF为BE边上的中线，求证：AF⊥CD；
（3）如图3，在（2）的条件下，AB=5，AE=4，DE=2，则五边形ABCDE的面积为______；点E到直线AB的距离为______.
24．（本题12分）平面直角坐标系中，已知A(a,0)，B(0,b)，且a、b满足a-3+(b-3)​2=0.
（1）请直接写出A、B两点的坐标；
（2）如图为1，点P为OA延长线上的动点，点N在x轴负半轴上运动，且始终满足AP=ON，过O作NB的垂线交AB的延长线于M，连接MP，探究线段NB、OM、MP之间的数量关系为__________，请证明你的结论；
（3）如图2，G为△AOB内一点，OG⊥BG，在GO的延长线上取点H，连接BH，若∠ABG=∠HBO，点G(2n,n)，求G点的坐标.