江苏省泰州市靖江外国语学校2024--2025学年八年级上学期第一次月考数学试卷

这是一份江苏省泰州市靖江外国语学校2024--2025学年八年级上学期第一次月考数学试卷，共10页。试卷主要包含了10）等内容，欢迎下载使用。
（时间120分钟 满分150分）
请注意：1．本试卷分选择题和非选择题两个部分；
2．所有试题的答案均填写在答题卡上，答案写在试卷上无效；
3．作图必须用2B铅笔，并请加黑加粗．
第一部分 选择题（共18分）
一、选择题（本大题共有6小题，每小题3分，共18分．在每小题所给出的四个选项中，只有一项符合题意，请将正确选项的字母代号填涂在答题卷相应位置上）
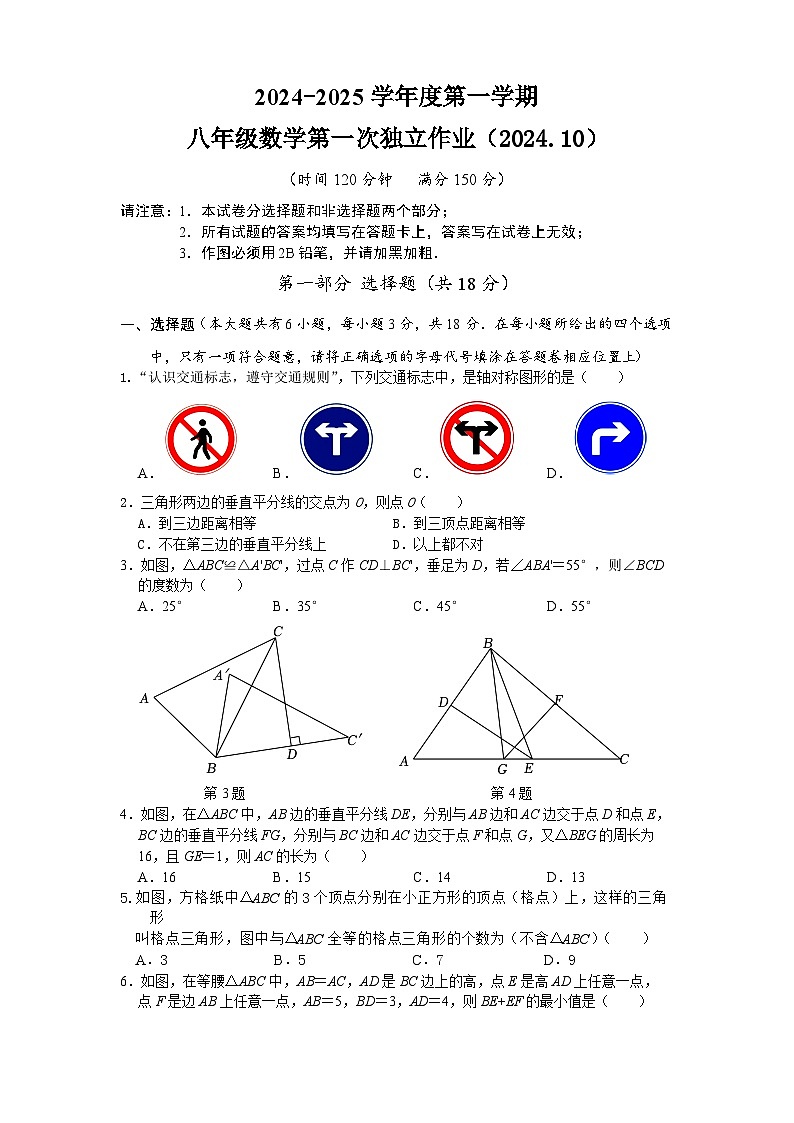
1.“认识交通标志，遵守交通规则”，下列交通标志中，是轴对称图形的是（ ）
A．B．C．D．
2．三角形两边的垂直平分线的交点为O，则点O（ ）
A．到三边距离相等 B．到三顶点距离相等
C．不在第三边的垂直平分线上 D．以上都不对
3．如图，△ABC≌△A'BC'，过点C作CD⊥BC'，垂足为D，若∠ABA'＝55°，则∠BCD的度数为（ ）
A．25°B．35°C．45°D．55°

第3题 第4题
4．如图，在△ABC中，AB边的垂直平分线DE，分别与AB边和AC边交于点D和点E，BC边的垂直平分线FG，分别与BC边和AC边交于点F和点G，又△BEG的周长为16，且GE＝1，则AC的长为（ ）
A．16B．15C．14D．13
5.如图，方格纸中△ABC的3个顶点分别在小正方形的顶点（格点）上，这样的三角形
叫格点三角形，图中与△ABC全等的格点三角形的个数为（不含△ABC）（ ）
A．3 B．5 C．7 D．9
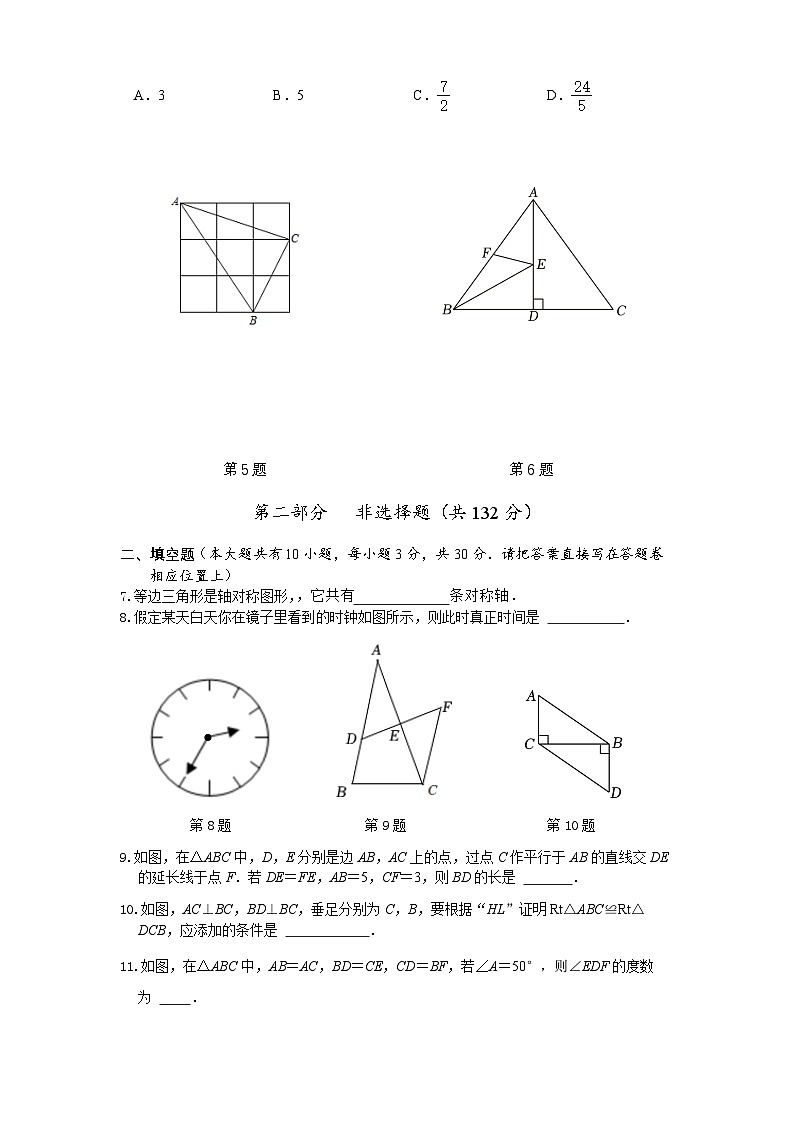
6．如图，在等腰△ABC中，AB＝AC，AD是BC边上的高，点E是高AD上任意一点，点F是边AB上任意一点，AB＝5，BD＝3，AD＝4，则BE+EF的最小值是（ ）
A．3B．5C．D．
第5题 第6题
第二部分 非选择题（共132分）
二、填空题（本大题共有10小题，每小题3分，共30分．请把答案直接写在答题卷相应位置上）
7.等边三角形是轴对称图形，，它共有 条对称轴．
8.假定某天白天你在镜子里看到的时钟如图所示，则此时真正时间是 ．

第8题 第9题 第10题
9.如图，在△ABC中，D，E分别是边AB，AC上的点，过点C作平行于AB的直线交DE的延长线于点F．若DE＝FE，AB＝5，CF＝3，则BD的长是 ．
10.如图，AC⊥BC，BD⊥BC，垂足分别为C，B，要根据“HL”证明Rt△ABC≌Rt△DCB，应添加的条件是 ．
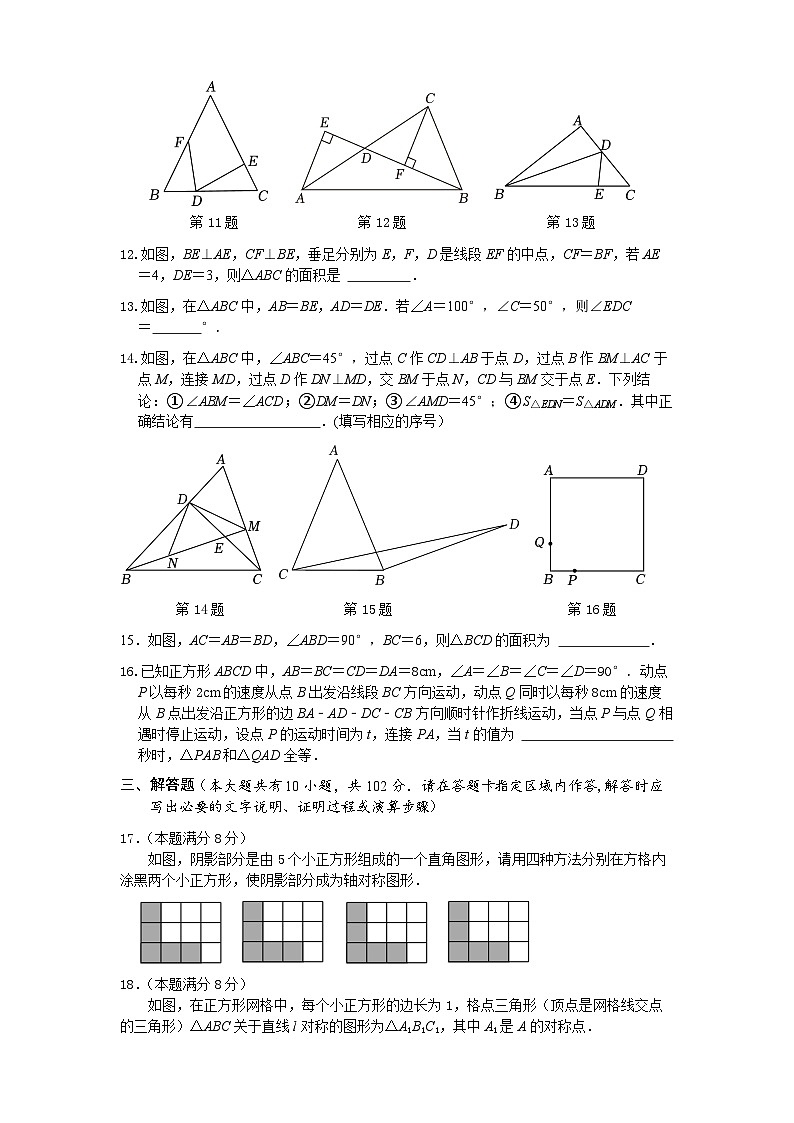
11.如图，在△ABC中，AB＝AC，BD＝CE，CD＝BF，若∠A＝50°，则∠EDF的度数为 ．


第11题 第12题 第13题
12.如图，BE⊥AE，CF⊥BE，垂足分别为E，F，D是线段EF的中点，CF＝BF，若AE＝4，DE＝3，则△ABC的面积是 ．
13.如图，在△ABC中，AB＝BE，AD＝DE．若∠A＝100°，∠C＝50°，则∠EDC＝ °．
14.如图，在△ABC中，∠ABC＝45°，过点C作CD⊥AB于点D，过点B作BM⊥AC于点M，连接MD，过点D作DN⊥MD，交BM于点N，CD与BM交于点E．下列结论：①∠ABM＝∠ACD；②DM＝DN；③∠AMD＝45°；④S△EDN＝S△ADM．其中正确结论有 ．(填写相应的序号）

第14题 第15题 第16题
15．如图，AC＝AB＝BD，∠ABD＝90°，BC＝6，则△BCD的面积为 ．
16.已知正方形ABCD中，AB＝BC＝CD＝DA＝8cm，∠A＝∠B＝∠C＝∠D＝90°．动点P以每秒2cm的速度从点B出发沿线段BC方向运动，动点Q同时以每秒8cm的速度从B点出发沿正方形的边BA﹣AD﹣DC﹣CB方向顺时针作折线运动，当点P与点Q相遇时停止运动，设点P的运动时间为t，连接PA，当t的值为 秒时，△PAB和△QAD全等．
三、解答题（本大题共有10小题，共102分．请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤）
17．（本题满分8分）
如图，阴影部分是由5个小正方形组成的一个直角图形，请用四种方法分别在方格内涂黑两个小正方形，使阴影部分成为轴对称图形．
18．（本题满分8分）
如图，在正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线交点的三角形）△ABC关于直线l对称的图形为△A1B1C1，其中A1是A的对称点．
（1）请作出对称轴直线l及△ABC关于直线l对称的△A1B1C1；
（2）在直线l上画出点P，使得△PAC的周长最小；
（3）直接写出四边形ABB1A1的面积为 ．
19．（本题满分8分）
已知：如图，点E、F在线段BD上，AF⊥BD，CE⊥BD，AD＝CB，DE＝BF，求证：AF＝CE．
20．（本题满分10分）
已知：如图，在四边形ABCD中，E是AC上一点，∠1＝∠2，∠3＝∠4．
求证：∠5＝∠6．
21．（本题满分10分）
如图，△ABC中，BD平分∠ABC，CD平分∠ACB，DE⊥AB于点E，DF⊥BC于点F．
（1）若∠A＝70°，求∠BDC的度数；
（2）若DE＝2，BC＝9，求△BCD的面积．
22．（本题满分10分）
如图，△ABC中，AD是BC边上的中线，E，F为直线AD上的点，连接BE，CF，且BE∥CF．
（1）求证：△BDE≌△CDF；
（2）若AE＝13，AF＝7，试求DE的长．
（本题满分12分）
如图，在△ABC中，∠ACB＝90°．
（1）作△ABC的角平分线BE，过点E作ED⊥AB，垂足为D；（要求：尺规作图，保留作图痕迹，不必写作法和证明.）
（2）在（1）的条件下，如果AC＝10cm，求AE+DE的值．
（本题满分12分）
如图，∠B＝∠C＝90°，E是BC的中点，DE平分∠ADC．
（1）若∠CDE＝55°，则∠CED＝ °；
（2）若∠BAE＝40°，则∠BAD＝ °；
（3）AE和DE的位置关系是 ，当AE＝6，DE＝8时，四边形ABCD的面积是 ；
（4）探索AB、CD、AD的数量关系，并加以证明．
25.（本题满分12分）
阅读：在同一个三角形中，如果两条边相等，那么它们所对的角也相等，简称“等边对等角”.
例如：如图1，在△ABC中，若AB＝AC，依据“等边对等角”可得∠B＝∠C.
运用上述知识，解决问题：
（1）在△ABC中，∠ACB＝90°，将△ABC绕点A逆时针旋转到△ADE（其中点B、C的对应点分别是点D、E）．
①如图2，当点C在AD上时，若∠ABC＝40°，则∠CBD的度数为 ；
②如图3，当点E在BA的延长线上时，延长BC交DE于点F，若AC＝5，BC＝12，AB＝13，求EF的长；

图1 图2 图3 图4
（2）如图4，已知△ABC和△DEF中，AB＝AC，DE＝DF，∠BAC＝∠EDF，点E在AB上，点F在射线AC上．若∠B＝70°，则∠DAF的度数为多少？
26.（本题满分12分）
如图，在△ABC中，∠ACB＝90°，AC＝BC，∠PCQ＝45°，把∠PCQ绕点C旋转，在整个旋转过程中，过点A作AD⊥CP，垂足为D，直线AD交CQ于E．
图① 图②
（1）如图①，当∠PCQ在∠ACB内部时，求证：AD+BE＝DE；
（2）如图②当CQ在∠ACB外部时，试探究线段AD、BE和DE的数量关系，并证明你的结论；
（3）在（1）的条件下，若CD＝18，S△BCE＝2S△ACD，则AE的长为 ．
2024-2025学年度第一学期阶段调研
八 年 级 数 学
参 考 答 案
选择题（每题3分,共18分）
填空题(每题3分,共30分)
7、 3 8、 9:25 9、 2 10、 AB=DC 11、 65°
12、 28 13、 50° 14、 ①②③④ 15、 9 16、 0.8或83
解答题（本题共10小题，共102分）
17. （8分）
18. （2+2+2+2分）
（1）如图，直线l和△A1B1C1即为所求．
（2）如图，连接A1C，交直线l于点P，
则点P即为所求．
（3）直接写出四边形ABB1A1的面积为 24 ．
19. （8分）
证明：∵DE＝BF，
∴DE+EF＝BF+EF；
∴DF＝BE；
在Rt△ADF和Rt△CBE中
，
∴Rt△ADF≌Rt△CBE（HL），
∴AF＝CE．
20. （10分）
证明：在△ABC与△ADC中，
，
∴△ABC≌△ADC（ASA），
∴CB＝CD，
在△ECD与△ECB中
，
∴△ECD≌△ECB（SAS），
∴∠5＝∠6．
21. （5+5分）
解：（1）∵BD平分∠ABC，CD平分∠ACB
∴∠DBC=12∠ABC，∠DCB=12∠ACB
∴∠BDC＝180°-∠DBC-∠DCB
＝180°- 12∠ABC - 12∠ACB
＝180°- 12(∠ABC +∠ACB )
∵∠A +∠ABC +∠ACB＝180°,∠A＝70°
∴∠BDC＝125°．
（2） ∵BD平分∠ABC，DE⊥AB，DF⊥BC，DE＝2
∴DF＝DE＝2．
∵BC＝9，
∴．
22. （5+5分）
（1）证明：∵AD是BC边上的中线，
∴BD＝CD，
∵BE∥CF，
∴∠DBE＝∠DCF，
在△BDE和△CDF中，
，
∴△BDE≌△CDF（ASA）；
（2）解：∵AE＝13，AF＝7，
∴EF＝AE﹣AF＝13﹣7＝6，
∵△BDE≌△CDF，
∴DE＝DF，
∵DE+DF＝EF＝6，
∴DE＝3．
23. （4+4+4分）
（1）如图，线段BE，ED为所求。
（2） ∵BE平分∠ABC， ED⊥AB，EC⊥BC
∴ED＝EC
∵AE+EC＝AC, AC＝10cm
∴AE+DE＝10 (cm)
24. （2+2+2+2+4分）
（1） 35°
（2） 80°
（3） AE⊥DE ， 48 ．
（4）AD＝CD+AB （证明略）
25.（2+5+5分）
（1）∠CBD的度数为 25°
（2）连接AF，由旋转得AE＝AC，∠AED＝∠ACB＝90°，
∴∠AEF＝∠ACF＝90°，
∴△AEF和△ACF是直角三角形，
在Rt△AEF和Rt△ACF中，
，
∴Rt△AEF≌Rt△ACF（HL），
∴CF＝EF，
设CF＝EF＝x，
∵AC＝5，BC＝12，AB＝13，
∴BF＝12+x，
∵S△BEF＝EF•AB＝BF•AC，
∴13x＝（12+x）×5，
解得：x＝，即EF＝；
（3）∠DAF的度数为70°（过程略）
26．（4+4+4分）
（1）证明略
（2）AD﹣BE＝DE （证明略）
（3）AE的长为 24
1
2
3
4
5
6
B
B
B
C
C
D