四川省绵阳市三台县2023-2024学年八年级下学期期中考试数学试卷(含答案)

这是一份四川省绵阳市三台县2023-2024学年八年级下学期期中考试数学试卷(含答案)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
（满分100分，考试时间90分钟）
一、选择题：（本大题共12个小题，每小题3分，共36分）
1. 下列二次根式中，可以与合并的是（ ）
A. B. C. D.
答案：B
2. 下列计算不正确的是（ ）
A. B.
C. D.
答案：D
3. 在平行四边形中，若，则的度数为（ ）
A. B. C. D.
答案：D
4. 满足下列条件时，△ABC不是直角三角形的是（ ）
A. B.
C ，BC＝4，AC＝5D. ∠A＝40°，∠B＝50°
答案：A
5. 正方形具有而菱形不一定具有的性质是（ ）
A. 对边相等B. 对角线相等C. 对角相等D. 对角线互相平分
答案：B
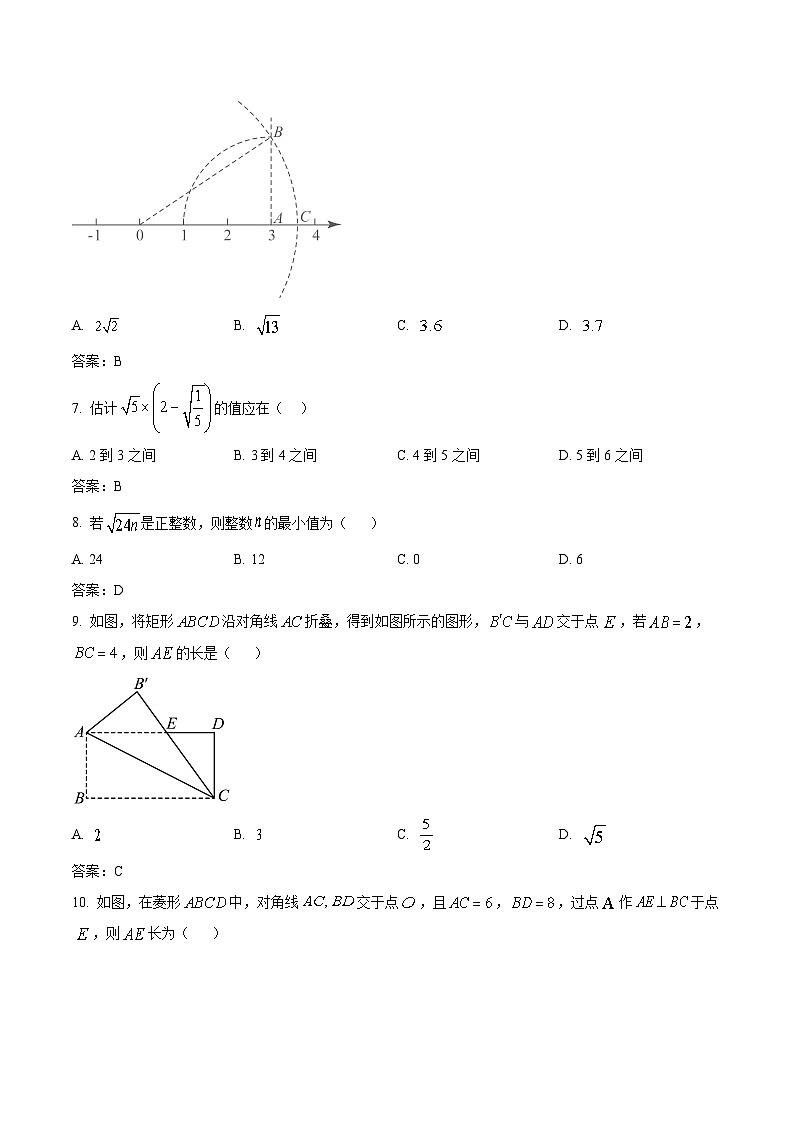
6. 如图，根据尺规作图的痕迹判断数轴上点所表示的数是( )

A. B. C. D.
答案：B
7. 估计的值应在（ ）
A. 2到3之间B. 3到4之间C. 4到5之间D. 5到6之间
答案：B
8. 若是正整数，则整数的最小值为（ ）
A. 24B. 12C. 0D. 6
答案：D
9. 如图，将矩形沿对角线折叠，得到如图所示的图形，与交于点，若，，则的长是（ ）
A. B. C. D.
答案：C
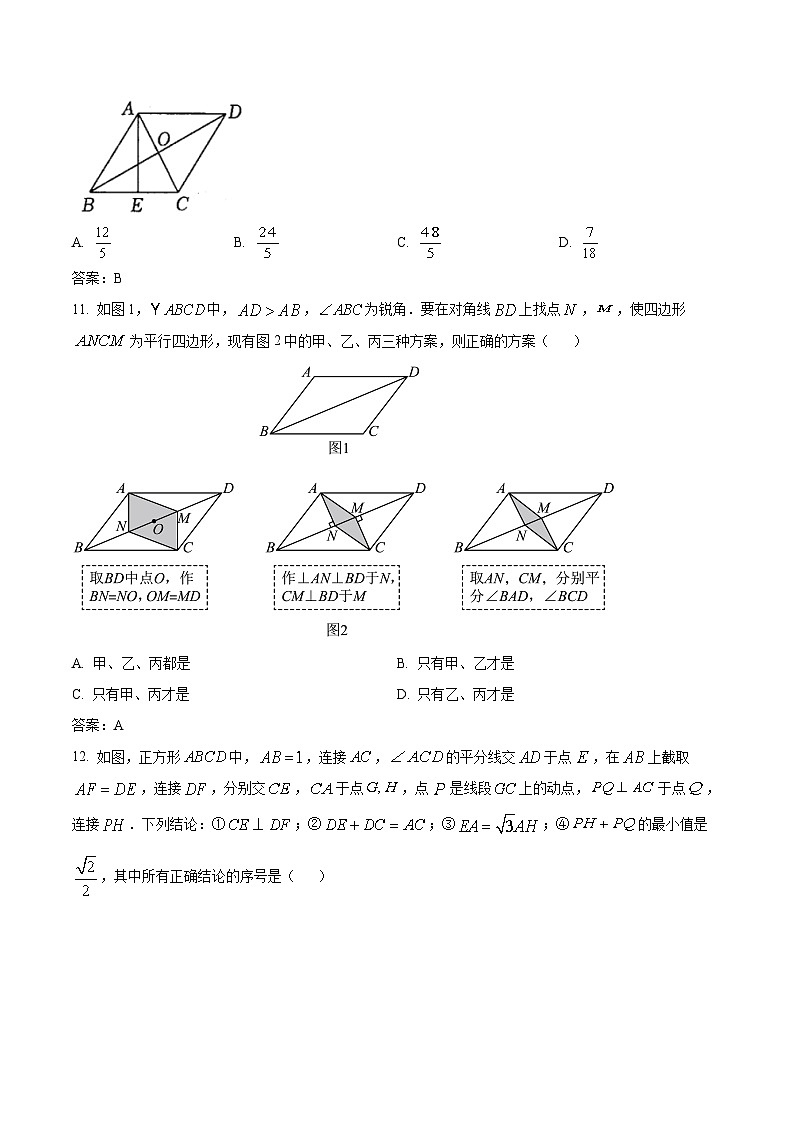
10. 如图，在菱形中，对角线交于点，且，，过点作于点，则长为（ ）
A. B. C. D.
答案：B
11. 如图1，中，，为锐角．要在对角线上找点，，使四边形为平行四边形，现有图2中的甲、乙、丙三种方案，则正确的方案（ ）
A. 甲、乙、丙都是B. 只有甲、乙才是
C. 只有甲、丙才是D. 只有乙、丙才是
答案：A
12. 如图，正方形中，，连接，的平分线交于点，在上截取，连接，分别交，于点，点是线段上的动点，于点，连接．下列结论：①；②；③；④的最小值是，其中所有正确结论的序号是（ ）
A. ①②③④B. ①②③C. ①②④D. ①③
答案：C
二、填空题：（每个小题3分，共18分）
13. 若二次根式有意义，则x的取值范围是_____．
答案：x≥1
14. 计算：______．
答案：
15. 如图，校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞___米．
答案：13
16. 若的整数部分为，小数部分为，则代数式______．
答案：##
17. 在中，若，，，则的面积是______．
答案：75或25
18. 如图，在菱形中，，为中点，点在延长线上，、分别为、中点，，，则_____．
答案：4
三、解答题：（共46分）
19. （1）计算：
（2）某校有一块形状为正方形的绿地，边长为米，现在要在正方形绿地内修建四个大小、形状相同的矩形花坛，每个花坛的长为米，宽为米，除去修建花坛的地方，其他地方全部修建成通道，通道上要铺上造价为元/平方米的地砖，如果要铺完整个通道，那么购买地砖需要花费多少元？（参考数据：）
答案：（1）；（2）元
解：（1）
原式
（2）通道的面积为：
（平方米）
购买地砖需要花费：元．
20. 如图，平行四边形的对角线、，相交于点，过点且与、分别相交于点、，求证：．
答案：见解析
证明：∵平行四边形ABCD的对角线AC、BD相交于点O，
∴AO＝CO，AB∥CD，
∴∠EAO＝∠FCO．
在△AOE和△COF中．
∴△AOE≌△COF（ASA）．
∴
21. 如图，四边形中，，，，．求的度数．
答案：
解析：连接，
∵，，
∴，，
∵，，
∴，
∴，
∴．
22. 如图，的对角线，相交于点，点，在上，且．
（1）求证：；
（2）过点作，垂足为，交于点，若的周长为12，求四边形的周长．
答案：（1）见解析 （2）24
【小问1详解】
证明：四边形是平行四边形，
，，
，
在与中，
，
，
，
，
；
【小问2详解】
解：由（1）知，，，
，
四边形是平行四边形，
，
，
，
的周长为12，
，
四边形的周长为24．
23. 人教版初中数学八年级下册第53页告诉我们直角三角形的一个性质：“直角三角形斜边上的中线等于斜边的一半”，我们一起来探究这条性质的证明过程：
（1）请你根据以上提示，结合图形，写出完整的证明过程．
（2）定理应用：如图2，Rt△ABC中，∠ACB＝90°，点D为边AC上一点，DE⊥AB于点E，连接BD，点M为BD的中点，CM的延长线交AB于点F，连接EC、EM．
①请直接写出线段CM与EM的数量关系________________；
②若BD是∠ABC的平分线，且∠BAC＝38°，则∠EMB＝________（直接写出结果无需证明）．
答案：（1）证明见解析
（2）①，②
【小问1详解】
证明：延长到，使，连接，，则，
∵是斜边上的中线，
∴，
∴四边形是平行四边形，
∵，
∴平行四边形是矩形，
∴，
∴；
【小问2详解】
解：①结论：CM=EM.
理由：∵DE⊥AB，
∴∠DEB=∠DCB=90°，
∵点M为BD中点
∴CM=DB，EM=DB，
∴CM=EM，
故答案为：CM=EM；
②∵∠ACB=90°，∠A=38°，
∴∠ABC=90°-38°=52°，
∵BD平分∠ABC，
∴∠ABD=×52°=26°，
∵DM=BM=EM，
∴∠MEB=∠MBE=26°，
∴∠EMB=180°-26°-26°=128°，
故答案：128°．
24. 已知四边形是矩形，连接．
（1）如图1，的平分线交于，交的延长线于点．的平分线交于点，交的延长线于点，连接．
①求证：；
②求证：四边形为菱形；
（2）在（1）的条件下，如图2，连接交于点，交于点，若，求的值．
答案：（1）①见解析；②见解析
（2）
【小问1详解】
证明：①四边形是矩形，
∴，
，
平分，
，
，
；
②由①知，，
，
平分，平分，
，，
，
，
，
，
由①知，，
，
平分，
，
，，
，
，
，
四边形是平行四边形，
，
是菱形；
【小问2详解】
解：点是矩形对角线与的交点，
，
，
是的中位线，
∴，
∵，
四边形是平行四边形，
，
四边形是矩形，
，，
，
由（1）②知，四边形是菱形，
，
，
在中，根据勾股定理得，，
．
如图1，在中，，是斜边上的中线．
求证：．
证明：延长至点，使，连结、．