福建省泉州台商投资区五校联考2024年数学九上开学统考模拟试题【含答案】

这是一份福建省泉州台商投资区五校联考2024年数学九上开学统考模拟试题【含答案】，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，在正方形中，点是的中点，点是的中点，与相交于点，设.得到以下结论：
①；②；③则上述结论正确的是（ ）
A．①②B．①③
C．②③D．①②③
2、（4分）若，则的值是（ ）
A．B．C．D．
3、（4分）若与最简二次根式是同类二次根式，则的值为（ ）
A．7B．9C．2D．1
4、（4分）下列平面图形中，是中心对称图形的是（ ）
A．B．C．D．
5、（4分）已知下面四个方程： +3x＝9；+1＝1；＝1；＝1．其中，无理方程的个数是( )
A．1B．2C．3D．4
6、（4分）已知点和点在反比例函数的图象上，若，则（ ）
A．B．
C．D．
7、（4分）如图，已知Rt△ABC中，∠ABC＝90°，分别以AB、BC、AC为直径作半圆，面积分别记S1，S2，S3，若S1＝4，S2＝9，则S3的值为( )
A．13B．5C．11D．3
8、（4分）下列给出的四个点中，在直线的是（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
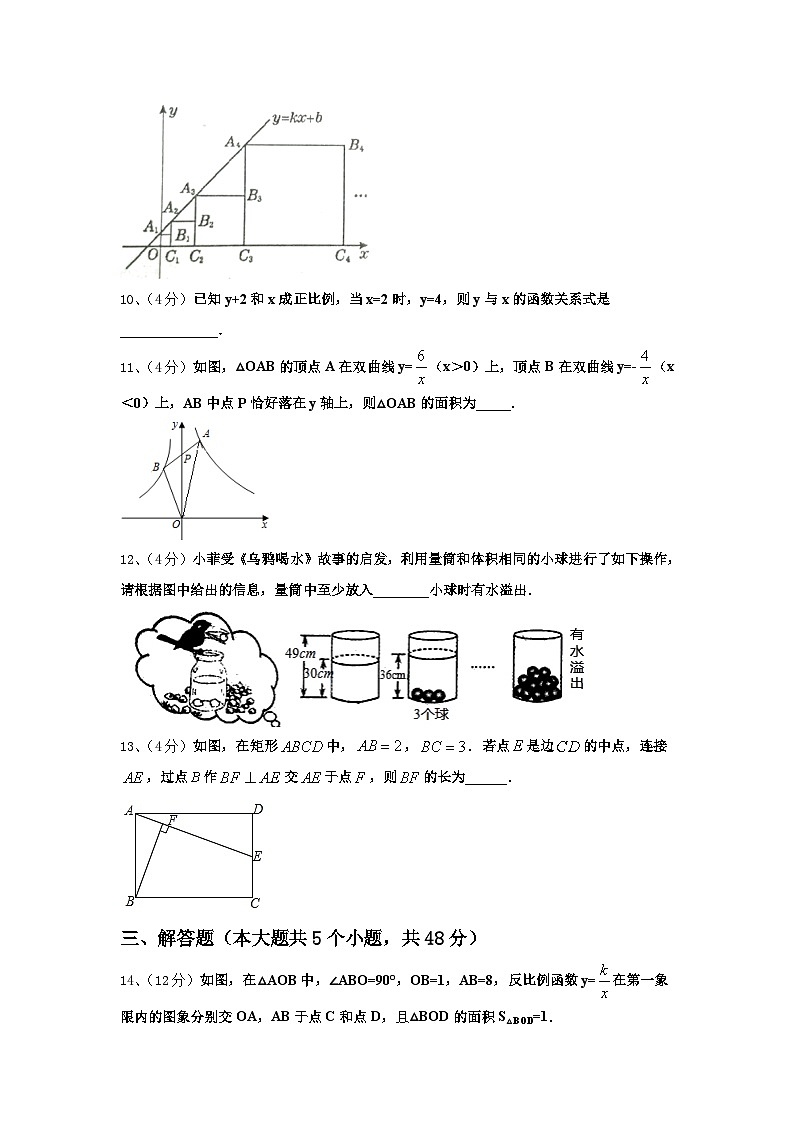
9、（4分）在平面直角坐标系中，正方形、正方形、正方形、正方形、…、正方形按如图所示的方式放置，其中点，，，，…，均在一次函数的图象上，点，，，，…，均在x轴上．若点的坐标为，点的坐标为，则点的坐标为______．
10、（4分）已知y+2和x成正比例，当x=2时，y=4，则y与x的函数关系式是______________．
11、（4分）如图，△OAB的顶点A在双曲线y=（x＞0）上，顶点B在双曲线y=-（x＜0）上，AB中点P恰好落在y轴上，则△OAB的面积为_____.
12、（4分）小菲受《乌鸦喝水》故事的启发，利用量筒和体积相同的小球进行了如下操作，请根据图中给出的信息，量筒中至少放入________小球时有水溢出．

13、（4分）如图，在矩形中，，．若点是边的中点，连接，过点作交于点，则的长为______．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在△AOB中，∠ABO=90°，OB=1，AB=8，反比例函数y=在第一象限内的图象分别交OA，AB于点C和点D，且△BOD的面积S△BOD=1．
（1）求反比例函数解析式；
（2）求点C的坐标．
15、（8分）如图，以△ABC的各边，在边BC的同侧分别作三个正方形ABDI，BCFE，ACHG．
（1）求证：△BDE≌△BAC；
（2）求证：四边形ADEG是平行四边形．
（3）直接回答下面两个问题，不必证明：
①当△ABC满足条件_____________________时，四边形ADEG是矩形．
②当△ABC满足条件_____________________时，四边形ADEG是正方形？
16、（8分）如图直线y＝2x+m与y＝(n≠0)交于A，B两点，且点A的坐标为(1，4)．
(1)求此直线和双曲线的表达式；
(2)过x轴上一点M作平行于y轴的直线1，分别与直线y＝2x+m和双曲线y＝(n≠0)交于点P，Q，如果PQ＝2QM，求点M的坐标．
17、（10分）列分式方程解应用题
“六一”前夕，某商场用7200元购进某款电动玩具销售．由于销售良好，过了一段时间，商场又用14800元购进这款玩具，所购数量是第一次购进数量的2倍，但每件价格比第一次购进贵了2元．
（1）求该商场第一次购进这款玩具多少件？
（2）设该商场两次购进的玩具按相同的标价销售，最后剩下的80件玩具按标价的六折再销售，若两次购进的玩具全部售完，且使利润不低于4800元，则每件玩具的标价至少是多少元？
18、（10分）如图(1)，公路上有A、B、C三个车站，一辆汽车从A站以速度v1匀速驶向B站，到达B站后不停留，以速度v2匀速驶向C站，汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示．
(1)当汽车在A、B两站之间匀速行驶时，求y与x之间的函数关系式及自变量的取值范围；
(2)求出v2的值；
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米，求这段路程开始时x的值．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）等边三角形的边长为6，则它的高是________
20、（4分）用反证法证明：“三角形中至少有两个锐角”时，首先应假设这个三角形中_____．
21、（4分）如图，△ACB和△DCE都是等腰直角三角形，CA＝CB，CD＝CE，∠ACB＝∠DCE＝90°，△ACB的顶点A在△DCE的斜边DE上，且AD＝，AE＝3，则AC＝_____．
22、（4分）如图，已知中，，，，是的垂直平分线，交于点，连接，则___
23、（4分）如果将直线平移，使其经过点，那么平移后所得直线的表达式是__________.
二、解答题（本大题共3个小题，共30分）
24、（8分）在▱ABCD中，点E、F分别在AB、CD上，且AE=CF．
（1）求证：△ADE≌△CBF；
（2）若DF=BF，求证：四边形DEBF为菱形．
25、（10分）某商店经销某种玩具，该玩具每个进价 20 元，为进行促销，商店制定如下“优惠” 方案：如果一次销售数量不超过 5 个，则每个按 50 元销售：如果一次销售数量超过 5 个，则每增加一个，所有玩具均降低 1 元销售，但单价不得低于 30 元，一次销售该玩具的单价 y（元）与销售数量 x（个）之间的函数关系如下图所示．
（1）结合图形，求出 m 的值；射线 BC 所表示的实际意义是什么；
（2）求线段 AB 满足的 y 与 x 之间的函数解析式，并直接写出自变量的取值范围；
（3）当销售 15 个时，商店的利润是多少元．
26、（12分）如图，在等腰梯形ABCD中，，，，.点Р从点B出发沿折线段以每秒5个单位长的速度向点C匀速运动；点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动，过点O向上作射线OKIBC，交折线段于点E．点P、O同时开始运动，为点Р与点C重合时停止运动，点Q也随之停止.设点P、Q运动的时间是t秒.
（1）点P到达终点C时，求t的值，并指出此时BQ的长；
（2）当点Р运动到AD上时，t为何值能使？
（3）t为何值时，四点P、Q、C、E成为一个平行四边形的顶点？
（4）能为直角三角形时t的取值范围________.（直接写出结果）
（注：备用图不够用可以另外画）

参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
由正方形的性质和全等三角形的判定与性质，直角三角形的性质进行推理即可得出结论．
【详解】
解：如图，
（1）
所以①成立
(2)如图延长交延长线于点，
则：
∴为直角三角形斜边上的中线，是斜边的一半，即
所以②成立
(3) ∵
∴
∵
∴
所以③成立
故选：D
本题考查的正方形的性质，直角三角形的性质以及全等三角形的判定和性质，解答此题的关键是熟练掌握性质和定理．
2、B
【解析】
解：
故选：B．
本题考查同分母分式的加法运算．
3、D
【解析】
先将化简为最简二次根式，，根据同类二次根式的定义得出a+1=2，求出a即可．
【详解】
∵与最简二次根式是同类二次根式
∴a+1=2
解得a=1
故选：D
本题考查了最简二次根式和同类二次根式的定义，满足下列两个条件的二次根式，叫做最简二次根式，被开方数不含分母，被开方数中不含能开得尽方的因数或因式；把几个二次根式化成最简二次根式以后，如果被开方数相同，那么这几个二次根式就叫做同类二次根式．
4、B
【解析】
根据中心对称图形的概念求解．
【详解】
解：A、不是中心对称图形，故此选项错误；
B、是中心对称图形，故此选项正确；
C、不是中心对称图形，故此选项错误；
D、不是中心对称图形，故此选项错误．
故选B．
本题考查中心对称图形．
5、A
【解析】
无理方程的定义是:根号下含有未知数的方程即为无理方程,根据定义即可判断.
【详解】
无理方程的定义是:根号下含有未知数的方程即为无理方程,根据定义只有第一个方程为无理方程.即+3x＝9，1个，
故选：A．
本题直接考查了无理方程的概念--根号下含有未知数的方程即为无理方程.准确掌握此概念即可解题..
6、D
【解析】
根据反比例函数的图像与性质逐项分析即可.
【详解】
∵k<0，
∴反比例函数的图像在二、四象限.
A.当点在第二象限，点在第四象限，且时，x1+x2>0，y1+y2>0，此时，故A错误；
B. 当点和点在第四象限时，x1+x2>0，y1+y2<0，此时，故B错误；
C. 当点和点在第四象限时，x1·x2>0，x1-x2<0，y1-y2<0，此时，故C错误；
D. ∵A、B、C均错误，
∴D正确.
故选D.
本题考查了反比例函数的图像与性质，反比例函数(k是常数，k≠0)的图像是双曲线，当k＞0，反比例函数图象的两个分支在第一、三象限,在每一象限内，y随x的增大而减小；当 k＜0，反比例函数图象的两个分支在第二、四象限,在每一象限内，y随x的增大而增大.
7、A
【解析】
由扇形的面积公式可知S1＝•π•AC2，S2＝•π•BC2，S3＝•π•AB2，在Rt△ABC中，由勾股定理得AC2+BC2＝AB2，即S1+S2＝S3；
【详解】
解：∵S1＝•π•AC2，S2＝•π•BC2，S3＝•π•AB2，
在Rt△ABC中，由勾股定理得AC2+BC2＝AB2，即S1+S2＝S3；
∵S1＝4，S2＝9，
∴S3＝1．
故选A．
本题考查勾股定理的应用，难度适中，解题关键是对勾股定理的熟练掌握及灵活运用，记住S1+S2＝S3.
8、D
【解析】
只需把每个点的横坐标即x的值分别代入，计算出对应的y值，然后与对应的纵坐标比较即可．
【详解】
解：A、当时，，则不在直线上；
B、当时，，则不在直线上；
C、当时，，则不在直线上；
D、当时，，则在直线上；
故选：D.
本题考查判断点是否在直线上，知识点是：在这条直线上的各点的坐标一定适合这条直线的解析式．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（2n-1-1，2n-1）
【解析】
首先求得直线的解析式，分别求得，，，…的坐标，可以得到一定的规律，据此即可求解．
【详解】
】解：∵B1的坐标为（1，1），点B2的坐标为（3，2），
∴正方形A1B1C1O边长为1，正方形A2B2C2C1边长为2，
∴A1的坐标是（0，1），A2的坐标是：（1，2），
代入y=kx+b得
，
解得：

则直线的解析式是：y=x+1．
∵A1B1=1，点B2的坐标为（3，2），
∴A1的纵坐标是1，A2的纵坐标是2．
在直线y=x+1中，令x=3，则纵坐标是：3+1=4=22；
则A4的横坐标是：1+2+4=7，则A4的纵坐标是：7+1=8=23；
据此可以得到An的纵坐标是：2n-1，横坐标是：2n-1-1．
故点An的坐标为 （2n-1-1，2n-1）．
故答案是：（2n-1-1，2n-1）．
本题主要考查了待定系数法求函数解析式，正确得到点的坐标的规律是解题的关键．
10、y=3x-1
【解析】
解：设函数解析式为y+1=kx，
∴1k=4+1，
解得：k=3，
∴y+1=3x，
即y=3x-1．
11、5.
【解析】
分别作BC⊥ y轴于点C，AD⊥ y轴于点D，由P为AB的中点，得到S△ADP=S△BCP，在由A，B都在反比例函数上得到面积，转换即可
【详解】
如图分别作BC⊥ y轴于点C，AD⊥ y轴于点D，
∵P为AB的中点，
∴S△ADP=S△BCP，
则S△ABO=S△ BOC+S△ OAC，
∵A在双曲线y=（x＞0）上，顶点B在双曲线y=-（x＜0）上，
∴S△ BOC=2，S△ OAD=3，则S△ABO=5，故答案为5
熟练掌握反比例函数上的点与坐标轴和原点围成的三角形面积为|k|和面积转换是解决本题的关键
12、10
【解析】
（36-20）÷3=2（cm）.
设放入x小球有水溢出，由题意得
2x+30>49, ∴x>9.5, ∴放入10小球有水溢出.
13、
【解析】
根据S△ABE=S矩形ABCD=3=•AE•BF，先求出AE，再求出BF即可．
【详解】
解：如图，连接BE．
∵四边形ABCD是矩形，
∴AB=CD=2，BC=AD=3，∠D=90°，
在Rt△ADE中，AE=
∵S△ABE=S矩形ABCD=3=•AE•BF，
∴BF=．
故答案为：.
本题考查矩形的性质、勾股定理、三角形的面积公式等知识，解题关键是灵活运用所学知识解决问题，用面积法解决有关线段问题是常用方法．
三、解答题（本大题共5个小题，共48分）
14、（1）反比例函数解析式为y=；（2）C点坐标为（2，1）
【解析】
（1）由S△BOD=1可得BD的长，从而可得D的坐标，然后代入反比例函数解析式可求得k，从而得解析式为y=；
（2）由已知可确定A点坐标，再由待定系数法求出直线AB的解析式为y=2x，然后解方程组即可得到C点坐标．
【详解】
（1）∵∠ABO=90°，OB=1，S△BOD=1，
∴OB×BD=1，解得BD=2，
∴D（1，2）
将D（1，2）代入y=,
得2=,
∴k=8，
∴反比例函数解析式为y=；
（2）∵∠ABO=90°，OB=1，AB=8，
∴A点坐标为（1，8），
设直线OA的解析式为y=kx，
把A（1，8）代入得1k=8，解得k=2，
∴直线AB的解析式为y=2x，
解方程组得或，
∴C点坐标为（2，1）.
15、（1）见解析；（2）见解析；（3）①∠BAC=135°；②∠BAC=135°且AC=
【解析】
（1）根据全等三角形的判定定理SAS证得△BDE≌△BAC；
（2）由△BDE≌△BAC，可得全等三角形的对应边DE=AG．然后利用正方形对角线的性质、周角的定义推知∠EDA+∠DAG=180°，易证ED∥GA；最后由“一组对边平行且相等”的判定定理证得结论；
（3）①根据“矩形的内角都是直角”易证∠DAG=90°．然后由周角的定义求得∠BAC=135°；
②由“正方形的内角都是直角，四条边都相等”易证∠DAG=90°，且AG=AD．由正方形ABDI和正方形ACHG的性质证得：ACAB．
【详解】
（1）∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形，∴AC=AG，AB=BD，BC=BE，∠GAC=∠EBC=∠DBA=90°，∴∠ABC=∠EBD（同为∠EBA的余角）．
在△BDE和△BAC中，∵，∴△BDE≌△BAC（SAS）；
（2）∵△BDE≌△BAC，∴DE=AC=AG，∠BAC=∠BDE．
∵AD是正方形ABDI的对角线，∴∠BDA=∠BAD=45°．
∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°，∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC，∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°，∴DE∥AG，∴四边形ADEG是平行四边形（一组对边平行且相等）．
（3）①当四边形ADEG是矩形时，∠DAG=90°．
则∠BAC=360°﹣∠BAD﹣∠DAG﹣∠GAC=360°﹣45°﹣90°﹣90°=135°，即当∠BAC=135°时，平行四边形ADEG是矩形；
②当四边形ADEG是正方形时，∠DAG=90°，且AG=AD．
由①知，当∠DAG=90°时，∠BAC=135°．
∵四边形ABDI是正方形，∴ADAB．
又∵四边形ACHG是正方形，∴AC=AG，∴ACAB，∴当∠BAC=135°且ACAB时，四边形ADEG是正方形．
本题综合考查了正方形的判定与性质，全等三角形的判定与性质，平行四边形的判定与性质等知识点．解题时，注意利用隐含在题干中的已知条件：周角是360°．
16、 (1)直线的解析式为y＝2x+2，反比例函数的解析式为y＝；(2)M(﹣3，0)或(2，0)．
【解析】
（1）利用待定系数法即可解决问题；
（2）设M（a，0），表示出P（a，2a+2），Q（a，），根据PQ=2QD，列方程|2a+2-|=|2×|，解得a=2，a=-3，即可得到结果．
【详解】
(1)∵y＝2x+m与(n≠0)交于A(1，4)，
∴，
∴，
∴直线的解析式为y＝2x+2，反比例函数的解析式为．
(2)设M(a，0)，
∵l∥y轴，
∴P(a，2a+2)，Q(a，)，
∵PQ＝2QM，
∴|2a+2﹣|＝|2×|，
解得：a＝2或a＝﹣3，
∴M(﹣3，0)或(2，0)．
本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．也考查了待定系数法求函数解析式．
17、（1）该商场第一次购进这款玩具100件；（2）每件玩具的标价至少是100元．
【解析】
（1）设该商场第一次购进这款玩具x件，则第二次购进这款玩具2x件，根据两次购得的单价的差值为2元列出分式方程；
（2）设每件玩具的标价为y元，根据利润不低于4800元列出不等式并解答．
【详解】
（1）设该商场第一次购进这款玩具x件，则第二次购进这款玩具2x件，
依题意得：
解得x＝100
经检验x＝100是原方程的解．
即该商场第一次购进这款玩具100件；
（2）设每件玩具的标价为y元，则
（100+200﹣80）y+80×60%y﹣7200﹣14800≥4800
解得y≥100
即每件玩具的标价至少是100元．
考查了分式方程的应用和一元一次不等式的应用．分析题意，找到合适的数量关系是解决问题的关键．
18、（1）y=100x，（0＜x＜3）；（2）120千米/小时；（3）这段路程开始时x的值是2.5小时．
【解析】
（1）根据函数图象设出一次函数解析式，运用待定系数法求出解析式即可；
（2）根据距离÷时间=速度计算；
（3）设汽车在A、B两站之间匀速行驶x小时，根据题意列出方程，解方程即可．
【详解】
（1）根据图象可设汽车在A、B两站之间匀速行驶时，y与x之间的函数关系式为y=kx，
∵图象经过（1，100），
∴k=100，
∴y与x之间的函数关系式为y=100x，（0＜x＜3）；
（2）当y=300时，x=3，
4﹣3=1小时，420﹣300=120千米，
∴v2=120千米/小时；
（3）设汽车在A、B两站之间匀速行驶x小时，则在汽车在B、C两站之间匀速行驶（﹣x）小时，
由题意得，100x+120（﹣x）=90，
解得x=0.5，
3﹣0.5=2.5小时．
答：这段路程开始时x的值是2.5小时．
点睛：本题考查的是一次函数的应用，正确读懂函数图象、从中获取正确的信息、掌握待定系数法求函数解析式的步骤是解题的关键，解答时，注意方程思想的灵活运用．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
根据等边三角形的性质：三线合一，利用勾股定理可求解高．
【详解】
由题意得底边的一半是3，再根据勾股定理，得它的高为=3，
故答案为3.
本题考查的是等边三角形的性质，勾股定理，解答本题的关键是掌握好等腰三角形的三线合一：底边上的高、中线，顶角平分线重合.
20、三角形三个内角中最多有一个锐角
【解析】
“至少有两个”的反面为“最多有一个”，据此直接写出逆命题即可．
【详解】
∵至少有两个”的反面为“最多有一个”，而反证法的假设即原命题的逆命题正确；
∴应假设：三角形三个内角中最多有一个锐角．
故答案为：三角形三个内角中最多有一个锐角
本题考查了反证法，注意逆命题的与原命题的关系．
21、
【解析】
由等腰三角形的性质可得AC=BC,DC=EC,∠DCE=∠ACB=90°,∠D=∠CED=45°,可证△ADC≌△BEC,可得AD=BE=,∠D=∠BEC=45°,由勾股定理可求AB=2，即可求AC的长。
【详解】
证明：如图，连接BE，
∵△ACB和△DCE都是等腰直角三角形
∴AC=BC,DC=EC,∠DCE=∠ACB=90°,∠D=∠CED=45°
∴∠DCA=∠BCE，且AC=BC，DC=EC，
∴△ADC≌△BEC(SAS)
∴AD=BE=,∠D=∠BEC=45°，
∴∠AEB=90°
∴AB==2
∵AB=BC
∴BC=，因为△ACB是等腰直角三角形，所以BC=AC=.
本题考查等腰直角三角形的性质、全等三角形的判定和性质，解题的关键是掌握等腰直角三角形的性质、全等三角形的判定和性质.
22、5
【解析】
由是的垂直平分线可得AD=CD，可得∠CAD=∠ACD，利用勾股定理逆定理可得∠ACB=90°由等角的余角相等可得：∠DCB=∠B，可得CD=BD，可知CD=BD=AD=
【详解】
解：∵是的垂直平分线
∴AD=CD
∴∠CAD=∠ACD
∵，，
又∵
∴
∴∠ACB=90°
∵∠ACD+∠DCB=90°, ∠CAB+∠B=90°
∴∠DCB=∠B
∴CD=BD
∴CD=BD=AD=
故答案为5
本题考查了线段垂直平分线、勾股定理逆定理以及等腰三角形的性质，掌握勾股定理逆定理及利用等腰三角形求线段是解题的关键.
23、
【解析】
根据平移不改变k的值可设平移后直线的解析式为y=x+b，然后将点（0，2）代入即可得出直线的函数解析式．
【详解】
解：设平移后直线的解析式为y=x+b，把（0，2）代入直线解析式得解得 b=2，
所以平移后直线的解析式为．
本题考查了一次函数图象与几何变换，待定系数法求一次函数的解析式，掌握直线y=kx+b（k≠0）平移时k的值不变是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、（1）见解析；（2）见解析
【解析】
试题分析：（1）首先根据平行四边形的性质可得AD=BC，∠A=∠C，再加上条件AE=CF可利用SAS证明△ADE≌△CBF；
（2）首先证明DF=BE，再加上条件AB∥CD可得四边形DEBF是平行四边形，又DF=FB，可根据邻边相等的平行四边形为菱形证出结论．
试题解析：（1）∵四边形ABCD是平行四边形，
∴AD=BC，∠A=∠C，
∵在△ADE和△CBF中，
，
∴△ADE≌△CBF（SAS）；
（2）∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∵AE=CF，
∴DF=EB，
∴四边形DEBF是平行四边形，
又∵DF=FB，
∴四边形DEBF为菱形．
考点：全等三角形的判定；菱形的判定；平行四边形的性质．
25、（1）25、当一次销售数量超过 25 个时，每个均按 30 元销售；（2）线段 AB 满足的 y 与 x 之间的函数解析式是 y=-x+55（5≤x≤25）；（3）此时商店的利润为300元.
【解析】
（1）根据单价不得低于30元,即可求出m,所以BC表示当销量超过 25 个时，每个均按 30 元销售,
（2）待定系数法即可求解,
（3）将x=15代入解析式中即可求解.
【详解】
（1）m=5+（50-30）÷1=25 ，
射线BC 所表示的实际意义为当一次销售数量超过25 个时，每个均按 30 元销售，
故答案为：25、当一次销售数量超过 25 个时，每个均按 30 元销售；
（2）设线段 AB 满足的 y 与 x 之间的函数解析式为 y=kx+b， ，得 ，
即线段 AB 满足的 y 与 x 之间的函数解析式是 y=-x+55（5≤x≤25）；
（3）当 y=15 时，15=-x+55，得 x=40，
∴此时商店的利润为：15×[40 -20]=300（元）
本题考查了一次函数实际应用问题,属于简单题,注意分段考虑函数关系是解题关键.
26、 (2) 秒，；（2）详见解析；（3）；（4）或．
【解析】
（2）把BA，AD，DC它们的和求出来再除以速度每秒5个单位就可以求出t的值，然后也可以求出BQ的长；
（2）如图2，若PQ∥DC，又AD∥BC，则四边形PQCD为平行四边形，从而PD=QC，用t分别表示QC，BA，AP，然后就可以得出关于t的方程，解方程就可以求出t；
（3）分情况讨论，当P在BA上运动时，E在CD上运动．0≤t≤20，QC的长度≤30，PE的长度>AD=75，QC（4）①当点P在BA（包括点A）上，即0②当点P、E都在AD（不包括点A但包括点D）上，即2025×3-30=45，
可知，点P在以QE=40为直径的圆的外部，故∠EPQ不会是直角．由∠PEQ<∠DEQ，可知∠PEQ一定是锐角．对于∠PQE，
∠PQE≤∠CQE，只有当点P与C重合，即t=35时，如图4，∠PQE=90°，△PQE为直角三角形．
【详解】
解：(2)t=(50+75+50)÷5=35(秒)时，点P到达终点C，
此时，QC=35×3=205，
∴BQ的长为235−205=30.
(2)如图2,若PQ∥DC，
∵AD∥BC，
∴四边形PQCD为平行四边形，
∴PD=QC，
由QC=3t，BA+AP=5t
得50+75−5t=3t,
解得t=.
∴当t=时,PQ∥DC.
(3)当P在BA上运动时，E在CD上运动.0⩽t⩽20，QC的长度⩽30，PE的长度>AD=75，QC当P点运动到AD上，E在AD上，且P在E的左侧时，P、Q、C. E为顶点的四边形是平行四边形，如图5，
∴PE=QC.
如图2,作DH⊥BC于H,AG⊥BC于G，
∠AGB=∠DHC=90∘
∴四边形AGHD是矩形，
∴GH=AD=75.AG=DH.
在△ABG和△DCH中，

∴△ABG≌△DCH，
∴BG=CH=(235−75)=30,
∴ED=3(t−20)
∵AP=5t−50，
∴PE=75−(5t−50)−3(t−20)=255−8t.
∵QC=3t，
∴255−8t=3t，
t=.
当P在E点的右侧且在AD上时，t⩽25，P、Q、C. E为直角梯形，
当P在CD上，E在AD上QE与PC不平行，P、Q、C. E不可能为平行四边形，
∴t=；
(4)①当点P在BA(包括点A)上,即0过点P作PG⊥BC于点G，则PG=PB⋅sinB=4t，
又有QE=4t=PG，易得四边形PGQE为矩形，此时△PQE总能成为直角三角形。
②当点P、E都在AD(不包括点A但包括点D)上，即20由QK⊥BC和AD∥BC可知，此时，△PQE为直角三角形，但点P、E不能重合，
即5t−50+3t−30≠75,解得t≠.③当点P在DC上(不包括点D但包括点C)，
即2525×3−30=45，可知，点P在以QE=40为直径的圆的外部，故∠EPQ不会是直角。由∠PEQ<∠DEQ，可知∠PEQ一定是锐角
对于∠PQE，∠PQE⩽∠C, 只有当点P与C
重合,即t=35时,如图4,∠PQE=90∘，△PQE为直角三角形。
综上所述,当△PQE为直角三角形时,t的取值范围是0故答案为：0本题考查四边形综合题，熟练掌握四边形的基本性质及计算法则是解题关键.
题号
一
二
三
四
五
总分
得分