专题02圆的方程及位置关系（考点清单）（含答案） 2024-2025学年高二数学上学期期中考点大串讲（苏教版2019选择性必修第一册）学案

这是一份专题02圆的方程及位置关系（考点清单）（含答案） 2024-2025学年高二数学上学期期中考点大串讲（苏教版2019选择性必修第一册）学案，文件包含专题02圆的方程及位置关系考点清单教师版2024-2025学年高二数学上学期期中考点大串讲苏教版2019选择性必修第一册学案docx、专题02圆的方程及位置关系考点清单学生版2024-2025学年高二数学上学期期中考点大串讲苏教版2019选择性必修第一册学案docx等2份学案配套教学资源，其中学案共53页， 欢迎下载使用。


【清单01】圆的方程
一、圆的标准方程
1.圆的基本要素：圆心和半径
2.圆的标准方程
一般地，如果平面直角坐标系中⊙C的圆心为C（a，b），半径为r（r>0），设M（x，y）为平面直角坐标系中任意一点，则点M在⊙C上的充要条件是CM=r，即（x−a）2+（y−b）2=r两边平方，得
（x−a）2+（y−b）2=r2，此式通常称为圆的标准方程．
二、圆的一般方程
1.当D2＋E2－4F＞0时，方程x2＋y2＋Dx＋Ey＋F＝0称为圆的一般方程，其圆心为eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(D,2)，－\f(E,2)))，半径为
r＝eq \f(1,2) eq \r(D2＋E2－4F).
当D2＋E2－4F=0时,方程x2＋y2＋Dx＋Ey＋F＝0表示点eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(D,2)，－\f(E,2))).
3.当D2＋E2－4F<0时,方程x2＋y2＋Dx＋Ey＋F＝0不表示任何图形.
【清单02】点与圆的位置关系
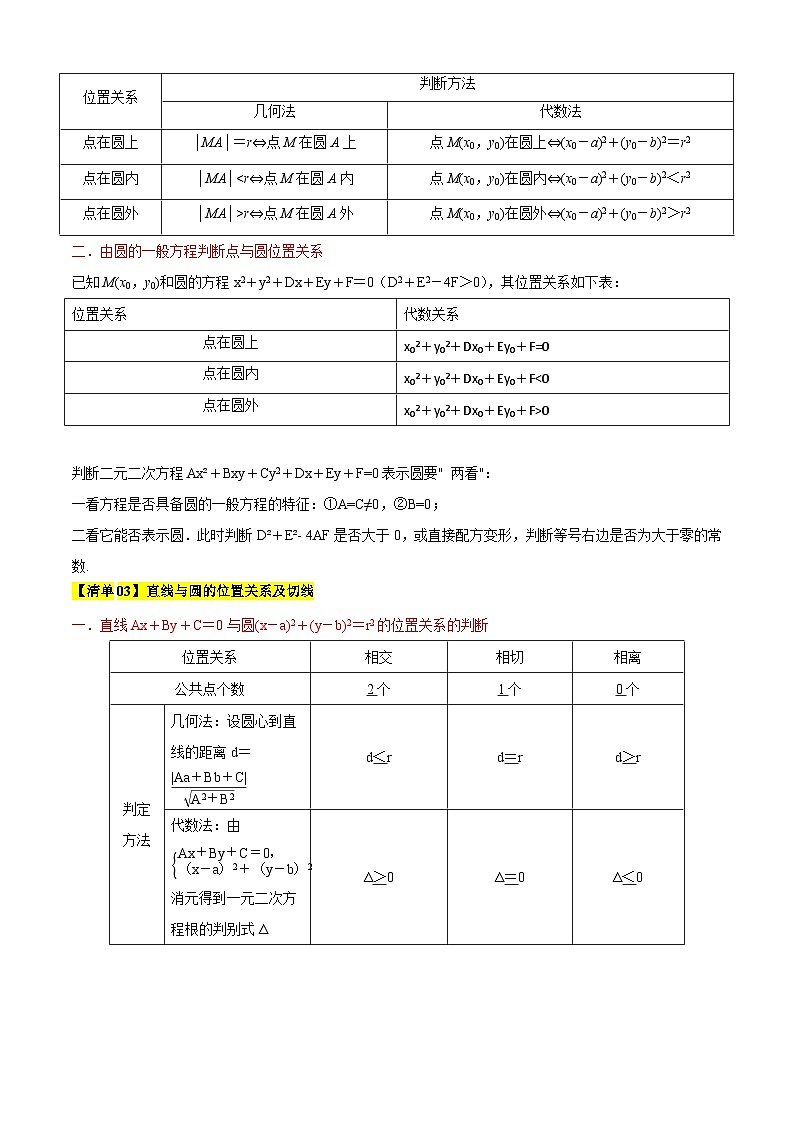
一．由圆的标准方程判断点与圆位置关系
圆的标准方程为(x－a)2＋(y－b)2＝r2，圆心A(a，b)，半径为r.设所给点为M(x0，y0)，则
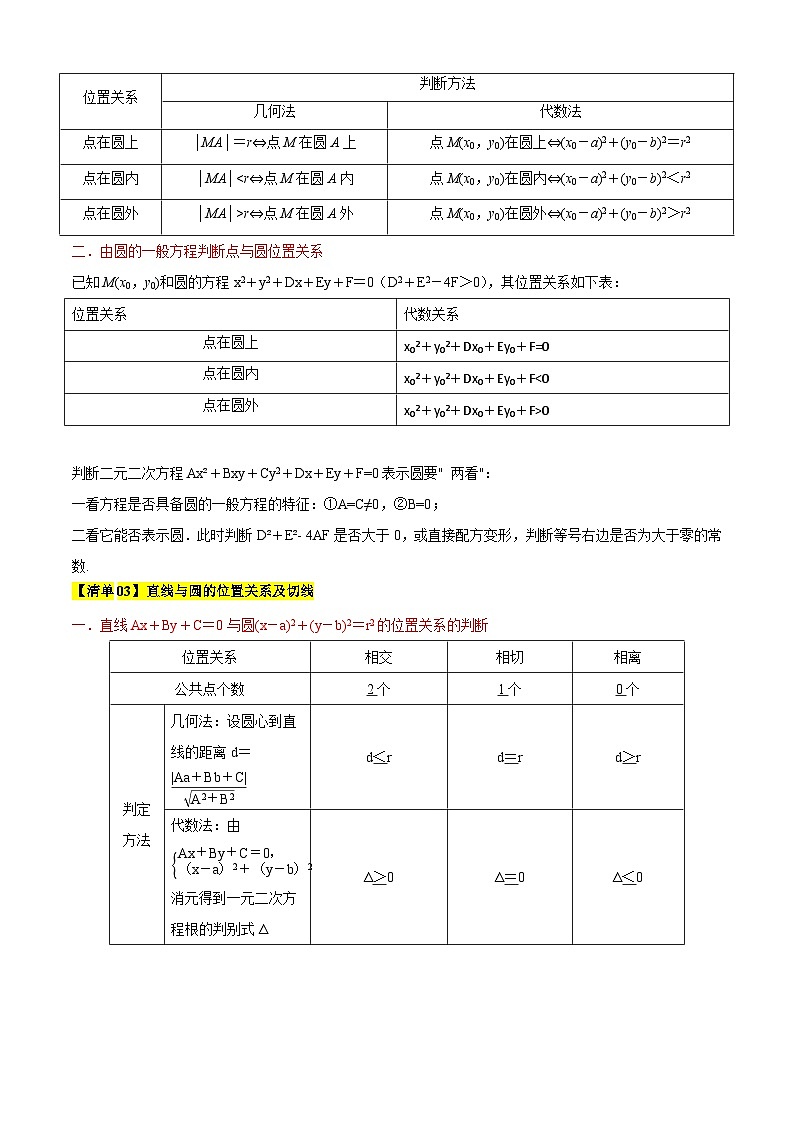
二．由圆的一般方程判断点与圆位置关系
已知M(x0，y0)和圆的方程x2＋y2＋Dx＋Ey＋F＝0（D2＋E2－4F＞0），其位置关系如下表：
判断二元二次方程Ax²＋Bxy＋Cy2＋Dx＋Ey＋F=0表示圆要" 两看"：
一看方程是否具备圆的一般方程的特征：①A=C≠0，②B=0；
二看它能否表示圆．此时判断D²＋E²- 4AF是否大于0，或直接配方变形，判断等号右边是否为大于零的常数.
【清单03】直线与圆的位置关系及切线
一．直线Ax＋By＋C＝0与圆(x－a)2＋(y－b)2＝r2的位置关系的判断
二．圆的切线
(1)过圆上一点的圆的切线
①过圆x2＋y2＝r2上一点M(x0，y0)的切线方程是x0x＋y0y＝r2.
②过圆(x－a)2＋(y－b)2＝r2上一点M(x0，y0)的切线方程是(x0－a)(x－a)＋(y0－b)(y－b)＝r2.
= 3 \* GB3 \* MERGEFORMAT ③过圆x2＋y2＝r2外一点M(x0，y0)作圆的两条切线，则两切点所在直线方程为x0x＋y0y＝r2.
(2)过圆外一点的圆的切线
过圆外一点M(x0，y0)的圆的切线求法：可用点斜式设出方程，利用圆心到直线的距离等于半径求出斜率k，从而得切线方程；若求出的k值只有一个，则说明另一条直线的斜率不存在，其方程为x＝x0.
三.切线长
①从圆x2＋y2＋Dx＋Ey＋F＝0(D2＋E2－4F>0)外一点M(x0，y0)引圆的两条切线，切线长为 eq \r(x\\al(2,0)＋y\\al(2,0)＋Dx0＋Ey0＋F).
②两切点弦长：利用等面积法，切线长a与半径r的积的2倍等于点M与圆心的距离d与两切点弦长b的积，即b＝eq \f(2ar,d).
注意：过一点求圆的切线方程时，要先判断点与圆的位置关系，以便确定切线的条数．
四．圆的弦长
直线和圆相交，求被圆截得的弦长通常有两种方法：
(1)几何法：因为半弦长eq \f(L,2)、弦心距d、半径r构成直角三角形，所以由勾股定理得L ＝2eq \r(r2－d2).
(2)代数法：若直线y＝kx＋b与圆有两交点A(x1，y1)，B(x2，y2)，则有：|AB|＝eq \r(1＋k2)|x1－x2|＝eq \r(1＋\f(1,k2))|y1－y2|.
【清单04】圆与圆的位置关系及切线、弦长
一.圆与圆的位置关系
圆与圆的位置关系有五种，分别为:外离、外切、相交、内切、内含。
二.圆与圆位置关系的判定
1.几何法
若两圆的半径分别为r1，r2，两圆的圆心距为d，则两圆的位置关系的判断方法如下：
2.代数法
通过两圆方程组成方程组的公共解的个数进行判断．
eq \b\lc\ \rc\}(\a\vs4\al\c1(圆C1方程,圆C2方程))eq \(――→,\s\up7(消元))一元二次方程eq \b\lc\{(\a\vs4\al\c1(Δ＞0⇒相交；,Δ＝0⇒内切或外切；,Δ＜0⇒内含或外离Ｗ.))
注意：涉及两圆相切时，没特别说明，务必要分内切和外切两种情况进行讨论．
注意：1.圆与圆相离，两圆无公共点，它包括外离和内含；
2.圆与圆相交，两圆有两个公共点；
3.圆与圆相切，两圆有且只有一个公共点，它包括内切和外切.
三. 两圆的公切线
两圆的公切线是指与两圆都相切的直线，可分为外公切线和内公切线. 两圆的公切线有如图所示的五种情况：
1.外离时，有4条公切线，分别是2条外公切线，2条内公切线；
2.外切时，有3条公切线，分别是2条外公切线，1条内公切线；
3.相交时，有2条公切线，都是外公切线；
4.内切时，有1条公切线；
5.内含时，无公切线.
四．两圆相交时公共弦所在直线的方程：
圆C1：x2＋y2＋D1x＋E1y＋F1＝0与C2：x2＋y2＋D2x＋E2y＋F2＝0相交时：
1.将两圆方程直接作差，得到两圆公共弦所在直线方程；
2.两圆圆心的连线垂直平分公共弦；
3.x2＋y2＋D1x＋E1y＋F1＋λ(x2＋y2＋D2x＋E2y＋F2)＝0表示过两圆交点的圆系方程(不包括C2)．
【考点题型一】圆的方程及解法
方法总结：
1.已知圆心坐标和半径，可以直接带入方程写出，在所给条件不是特别直接的情况下，关键是求出a，b，r的值再代入，
2.一般求圆的标准方程主要使用待定系数法:步骤如下:
(1)根据题意设出圆的标准方程为(x-a)2+(y-b)2=r2
(2)根据已知条件，列出关于a，b，r的方程组;
(3)求出a，b，r的值，代入所设方程中即可
另外，通过对圆的一般方程进行配方，也可以化为标准方程
【例1】（23-24高二上·吉林长春·期中）圆心在x轴上，并且过点A−1,3和B1,1的圆的标准方程是（ ）
A．x+42+y2=18B．x+32+y2=10
C．x−22+y2=10D．x+22+y2=10
【答案】D
【分析】设圆心为Ea,0，由EA=EB可求出a的值，可得出圆心的坐标，再求出圆的半径，即可得出所求圆的标准方程.
【详解】设圆心为Ea,0，由EA=EB可得a+12+0−32=a−12+0−12，解得a=−2，
所以，圆心为E−2,0，圆的半径为EA=−2−12+0−12=10，
故所求圆的标准方程为x+22+y2=10.
故选：D.
【变式1-1】（23-24高二上·江苏常州·期中）与两坐标轴都相切，且圆心在直线2x−y+6=0上的圆的标准方程是 ．
【答案】x+22+y−22=4或x+62+y+62=36
【分析】设所求圆的标准方程为x−a2+y−b2=a2，由题意可得b=±a，分b=a、b=−a两种情况讨论，根据圆心在直线2x−y+6=0上，求出a的值，即可得出所求圆的标准方程.
【详解】设所求圆的标准方程为x−a2+y−b2=a2，
因为所求圆与两坐标轴都相切，则b=±a，
当b=a时，则圆心a,a在直线2x−y+6=0上，则2a−a+6=a+6=0，解得a=−6，
此时，所求圆的标准方程为x+62+y+62=36；
当b=−a时，则圆心a,−a在直线2x−y+6=0上，则2a+a+6=3a+6=0，解得a=−2，
此时，所求圆的标准方程为x+22+y−22=4.
综上所述，所求圆的标准方程为x+22+y−22=4或x+62+y+62=36.
故答案为：x+22+y−22=4或x+62+y+62=36.
【变式1-2】（23-24高二上·江苏常州·期中）已知△ABC的顶点为A0，2，B6，4，C4，0．
(1)求边AC的垂直平分线的一般式方程；
(2)求△ABC的外接圆的方程．
【答案】(1)2x−y−3=0
(2)(x−3)2+(y−3)2=10
【分析】（1）求出直线AC的斜率，可得出AC边上的高所在直线的斜率，利用点斜式方程可得结果；
（2）设△ABC的外接圆的方程为x2+y2+Dx+Ey+F=0，将该三角形的三个顶点坐标代入所求圆的方程，可得出关于D,E,F的方程组，解出这三个未知数的值，即可得出△ABC的外接圆的方程.
【详解】（1）设AC中点为D，所以D0+42,2+02，即D2,1，
由题意得kAC=0−24−0=−12，所以边AC上高的斜率为2，
又因为AC的垂直平分线过点D2,1，
所以AC的垂直平分线的方程为：y−1=2x−2，即2x−y−3=0．
（2）设△ABC的外接圆的方程为x2+y2+Dx+Ey+F=0．
将A，B，C三点坐标代入上式得2E+F+4=0，6D+4E+F+52=04D+F+16=0，，解得D=−6E=−2F=8，
所以圆M的方程为x2+y2−6x−6y+8=0，即(x−3)2+(y−3)2=10．
【变式1-3】（23-24高二上·江西·阶段练习）若圆x2+y2−4x+8y+2m=0的半径为2，则实数m的值为（ ）
A．-9B．-8
C．9D．8
【答案】D
【分析】由圆的一般方程配方得出其标准方程，由半径为2得出答案.
【详解】由x2+y2−4x+8y+2m=0，得(x−2)2+(y+4)2=20−2m，
所以r=20−2m=2，解得m=8.
故选：D.
【变式1-4】（22-23高二上·江苏南通·期中）已知圆M：x2+y2−6x+2y+5=0，则该圆的圆心坐标为（ ）
A．−3,1B．−3,−1
C．3,1D．3,−1
【答案】D
【分析】把一般方程化为标准方程即可求解
【详解】圆M：x2+y2−6x+2y+5=0化为标准方程得
x−32+y+12=5，
所以圆心坐标为3,−1，
故选：D
【考点题型二】圆的一般方程
方法总结：x2＋y2＋Dx＋Ey＋F＝0表示的图形
【例2】（23-24高二上·浙江舟山·阶段练习）若a∈−2,−1,0,12,34,1 ，则方程x2+y2+ax+2ay+2a2+a−1=0表示的圆的个数为（ ）
A．1B．2
C．3D．4
【答案】C
【分析】由圆的一般方程表示圆的条件计算即可.
【详解】由题意可知：a2+2a2−42a2+a−1=−3a2−4a+4>0⇒3a−2a+2<0，
解之得−2又a∈−2,−1,0,12,34,1，所以a∈−1,0,12.
故选：C
【变式2-1】（22-23高二上·江苏苏州·期中）曲线x2+y2=2x−1+2y+2x−1所围成图形面积为 ．
【答案】4π+8
【分析】分情况去掉绝对值，从而可作出曲线的图像，进而求得面积.
【详解】分四种情况讨论：
①当x<1,y<0时，方程可化为：x2+(y+1)2=2，
表示圆心为(0,−1)，半径为2的圆；
②当x<1,y≥0时，方程可化为：x2+(y−1)2=2，
表示圆心为(0,1)，半径为2的圆；
③当x≥1,y<0时，方程可化为：(x−2)2+(y+1)2=2，
表示圆心为(2,−1)，半径为2的圆；
④当x≥1,y≥0时，方程可化为：(x−2)2+(y−1)2=2，
表示圆心为(2,1)，半径为2的圆.
作出图像如下图所示：
由图可知：曲线所围成图形为四个半圆和一个正方形所组成的区域，
正方形边长和圆的直径相等，
所以S=2×π×(2)2+(22)2=4π+8.
故答案为：4π+8.
【变式2-2】（23-24高二上·江苏南通·期中）若方程x2+y2+4mx−2y+4m2−m=0表示一个圆，则实数 m的取值范围是（ ）
A．m<−1B．m<1
C．m>−1D．m≥−1
【答案】C
【分析】若二元二次方程x2+y2+Dx+Ey+F=0表示圆，则必须满足D2+E2−4F>0.
【详解】由D2+E2−4F>0，
得(4m)2+(−2)2−4(4m2−m)>0，
即4m+4>0,
解得m>−1.
故选：C.
【变式2-3】（23-24高二上·江苏镇江·期中）已知抛物线y=x2−4x+3与x轴交于A,B（其中点B在点A的右边），与y轴交于点C，记△ABC的外接圆为圆M.
(1)求圆M的方程；
(2)经过点B的直线l与圆M的另一个交点为P，若PB=AC，求直线l的方程.
【答案】(1)x2+y2−4x−4y+3=0
(2)3x−y−9=0或x+3y−3=0
【分析】（1）求出点A,B,C的坐标，再设出圆的方程，利用待定系数法求解即可；
（2）求出AC，设出直线方程，然后利用垂径定理列方程求解.
【详解】（1）对于抛物线y=x2−4x+3
令y=0得x=1或x=3，即A1,0,B3,0，
令x=0得y=3，即C0,3
设圆的方程为x2+y2+Dx+Ey+F=0，
所以1+D+F=09+3D+F=09+3E+F=0，解得D=−4,E=−4,F=3，
故圆M的方程为x2+y2−4x−4y+3=0；
（2）由（1）得圆M的标准方程为x−22+y−22=5，圆心为2,2，半径为5，
又PB=AC=1+9=10，
当直线l斜率不存在时，PB=1，舍去，
当直线l斜率存在时，设为y=kx−3，即kx−y−3k=0，
则PB22=52−2k−2−3kk2+12，解得k=3或k=−13，
即直线l的方程为3x−y−9=0或x+3y−3=0
【变式2-4】（22-23高二上·江苏泰州·期中）若圆C的方程为x2+y2+2mx+4y+4m−95=0，则圆C的最小周长为（ ）
A．36π5B．185π5
C．125π5D．65π5
【答案】D
【分析】根据圆的方程求出圆的半径的最小值，即可求得答案.
【详解】因为圆C的方程为x2+y2+2mx+4y+4m−95=0，
故(2m)2+16−4(4m−95)=4(m−2)2+365≥365 ，m=2时取等号，
故圆的半径的最小值为12×365=355 ，
则圆C的最小周长为2π×355=65π5，
故选：D.
【考点题型三】点与圆的位置关系
方法总结：
【例3】（22-23高二上·江苏淮安·期中）圆(x−1)2+(y−2)2=2上的点P到点Q(4，−2)的距离可能为（ ）
A．3B．5
C．7D．9
【答案】B
【分析】求出圆心到点Q的距离d，则距离在d−r,d+r之间，选项一一比较即可.
【详解】设圆心为O，半径为r，坐标为1,2，则d=OQ=4−12+−2−22=5，所以距离范围为d−r,d+r，即5−2,5+2，而5在此范围内，
故选：B.
【变式3-1】（23-24高二上·江苏常州·期中）若点P(a,b)在圆C：x2+y2=1内，则直线ax+by=1与圆C的位置关系为（ ）
A．相交B．相切
C．相离D．不能确定
【答案】C
【分析】根据点与圆，直线与圆位置关系计算即可判断.
【详解】因为点Pa,b在圆C:x2+y2=1内，
所以a2+b2<1，
设圆心C0,0到直线ax+by=1的距离为d,
则d=0a+0b−1a2+b2=1a2+b2>1，
圆C:x2+y2=1的半径r=1,
因为d>r，所以直线ax+by=1与圆C的位置关系为相离.
故选：C.
【变式3-2】（多选）（23-24高二下·江苏南京·期中）点P3,a关于直线x+y−a=0的对称点在圆x−22+y−42=13内，则实数a可以为（ ）
A．4B．6
C．8D．10
【答案】BC
【分析】利用轴对称的性质，算出点P3,a关于直线x+y−a=0的对称点Q的坐标，然后根据点Q在圆内建立关于a的不等式，解出a的取值范围，即可得到本题的答案．
【详解】设点P3,a关于直线x+y−a=0的对称点为Qx,y，
则y−ax−3⋅−1=−13+x2+a+y2−a=0，得x=0y=a−3，即Q0,a−3，
若点Q在圆x−22+y−42=13内，则0−22+a−3−42<13，解得：4对照各个选项，可知B、C两项符合题意．
故选：BC．
【变式3-3】（多选）（22-23高二上·江苏盐城·期中）已知圆M：x2+y2−4x−1=0，则下列说法正确的是（ ）
A．点4,0在圆M外B．圆M的半径为5
C．直线x+y=0截圆M的弦长为3D．圆M关于x+3y−2=0对称
【答案】BD
【分析】将圆的方程标准化即可判断B项，运用比较已知点到圆心的距离与半径即可判断A项，由弦长公式计算可判断C项，由直线是否过圆心可判断D项.
【详解】因为x2+y2−4x−1=0⇒(x−2)2+y2=5，
所以圆心坐标为(2,0)，半径为r=5，故B项正确；
对于A项，因为点(4,0)到圆心的距离d=(4−2)2+02=2所以点(4,0)在圆M内，故A项错误；
对于C项，因为圆心到直线的距离为d=|2|12+12=2，
所以弦长为2r2−d2=2×5−2=23，故C项错误；
对于D项，因为直线x+3y−2=0过圆M的圆心(2,0)，
所以圆M关于x+3y−2=0对称，故D项正确.
故选：BD.
【变式3-4】（多选）（23-24高二上·江苏宿迁·期中）已知圆C：x−3k2+y−4k+12=1+25k2，则下列结论中正确的有（ ）
A．圆C过定点B．点0,0在圆C外
C．直线4x−3y−3=0平分圆周D．存在实数k，使圆与x轴相切
【答案】ACD
【分析】选项A，将圆的方程化简得到x2+y2+2y−k(6x+8y+8)=0，再由x2+y2+2y=06x+8y+8=0即可求出圆过点；
选项B，利用点与圆位置关系的判断方法即可判断出选项的正误；
选项C，根据条件，可得圆心(3k,4k−1)在直线4x−3y−3=0上，从而可判断出选项C的正误；
选项D，根据条件可得4k−1=1+25k2，从而求出k，即可解决问题.
【详解】对于选项A，由x−3k2+y−4k+12=1+25k2，得到x2−6kx+9k2+y2−2(4k−1)y+16k2−8k+1=1+25k2，
整理得到x2+y2+2y−k(6x+8y+8)=0，
由x2+y2+2y=06x+8y+8=0，得到x=−45y=−25或x=45y=−85，故圆C过定点(−45,−25)和(45,−85)，所以选项A正确；
对于选项B，因为圆心为(3k,4k−1)，r=1+25k2，
点0,0到圆心的距离d=9k2+16k2−8k+1=1+25k2−8k，
又因为k∈R，当k>0时，d对于选项C，因为圆心为(3k,4k−1)，又4×3k−3(4k−1)−3=0，即圆心在直线4x−3y−3=0上，所以选项C正确；
对于选项D，若圆与x轴相切，则有4k−1=1+25k2，即9k2+8k=0，解得k=0或k=−89，所以选项D正确，
故选：ACD.
【考点题型四】直线与圆的位置关系
方法总结：直线与圆的位置关系的判断方法
若给出图形，可根据公共点的个数判断;若给出直线与圆的方程，可选择用几何法或代数法，几何法计算量小，代数法可一同求出交点.解题时可根据条件作出恰当的选择.
【例4】（23-24高二上·江苏淮安·期中）已知点P(m,n)在圆O:x2+y2=6外，则直线mx+ny=6与圆O的位置关系为（ ）
A．相交B．相切
C．相离D．无法确定
【答案】A
【分析】利用圆心到直线的距离与半径进行比较，从而求解.
【详解】由点P(m,n)在圆O:x2+y2=6外，得：m2+n2>6，
圆心O0,0到直线的距离：d=6m2+n2<6，
所以得：直线mx+ny=6与圆O相交，故A项正确.
故选：A
【变式4-1】（23-24高二上·江苏南京·期中）在平面直角坐标系xOy中，已知点A3,0，动点Px,y满足PAPO=2，则动点P的轨迹与圆x−12+y−12=1的位置关系是（ ）
A．外离B．外切
C．相交D．内切
【答案】C
【分析】利用已知条件列出方程，化简可得点P的轨迹方程为圆，再判断圆心距和半径的关系即可得解.
【详解】由PAPO=2，得PA=2PO，
则x−32+y2=2x2+y2，整理得x+12+y2=4，
表示圆心为(−1,0)，半径为R=2的圆，
圆x−12+y−12=1的圆心为(1,1)为圆心，半径r=1，
两圆的圆心距为−1−12+0−12=5，满足2−1<5<2+1，
所以两个圆相交.
故选：C.
【变式4-2】（23-24高二上·江苏南通·期中）直线ax+y−a+1=0a∈R与圆x2+y2=4的位置关系为（ ）
A．相交B．相切
C．相离D．三种关系均存在
【答案】A
【分析】根据直线方程得到直线恒过定点1,−1，然后根据点1,−1在圆内得到直线与圆相交.
【详解】直线ax+y−a+1=0可整理为ax−1+y+1=0，
令x−1=0y+1=0，解得x=1y=−1，所以直线ax+y−a+1=0恒过定点1,−1，
因为12+−12<4，所以点1,−1在圆内，
所以直线ax+y−a+1=0与圆相交.
故选：A.
【变式4-3】（23-24高二上·江苏·期中）若直线l:kx−y−2=0与曲线C:1−(y−1)2=x−1有两个交点，则实数k的取值范围是（ ）
A．43,2B．43,4
C．−2,43∪43,2D．43,+∞
【答案】A
【分析】先求出直线l:kx−y−2=0所过的定点(0,−2)，再将曲线1−(y−1)2=x−1转化为x−12+(y−1)2=1x≥1，可知其为半圆，结合图象，即可求出k的取值范围.
【详解】直线l:kx−y−2=0恒过定点(0,−2)，
将1−(y−1)2=x−1转化为x−12+(y−1)2=1x≥1，
∴曲线C:1−(y−1)2=x−1表示以(1,1)为圆心，半径为1，且位于直线x=1右侧的半圆（包括点(1,2)，(1,0)），
当直线l经过点(1,0)时，l与曲线C有两个不同的交点，此时k=2，直线记为l1；
当l与半圆相切时，由|k−3|k2+1=1，得k=43，切线记为l2，
当43故选：A.
【变式4-4】（22-23高二上·江苏宿迁·期中）直线y=−x+1与曲线x=1−y2的交点个数为（ ）
A．0B．1
C．2D．3
【答案】C
【分析】联立方程后考虑方程组的解，从而可得交点的个数.
【详解】联立直线方程和曲线方程可得y=−x+1x=1−y2可得1−y=1−y2，
即y≤1y2−y=0，解得y=0或y=1，故方程组的解为x=1y=0或x=0y=1.
故选：C
【考点题型五】圆的切线
方法总结：求过某一点的圆的切线方程
(1)点(x0，y0)在圆上
①先求切点与圆心连线的斜率k，再由垂直关系得切线的斜率为-1k，由点斜式可得切线方程
②)如果斜率为零或不存在，则由图形可直接得切线方程y=y0或x=x0
(2)点(x0，y0)在圆外.
①设切线方程为y-y0=k(x-x0)，由圆心到直线的距离等于半径建立方程，可求得k，也就得切线方程
②当用此法只求出一个方程时，另一个方程应为x=x，因为在上面解法中不包括斜率不存在的情况
【例5】（23-24高二上·江苏宿迁·期中）已知圆C:x2+y2+2x−2y=0，直线l的过点1,−1且与圆C相切，则满足条件的直线l有几条（ ）
A．1B．2
C．3D．4
【答案】B
【分析】先判断1,−1与圆的位置关系，然后可判断出切线条数.
【详解】因为圆心为−1,1，半径r=2，
所以1,−1到−1,1的距离为22+−22=22>r，
所以1,−1在圆外，
过圆外一点作圆的切线有2条，
故选：B.
【变式5-1】（23-24高二上·江苏无锡·期中）已知圆C:x2+y2−2x=0,过P−1,2作圆C的切线,则切线长为（ ）
A．5B．7
C．3D．4
【答案】B
【分析】根据圆的方程求出圆心与半径r,利用两点间的距离公式求得PC,从而切线长为PC2−r2,计算求解即可.
【详解】圆C:x2+y2−2x=0,即x−12+y2=1,∴圆心C1,0,半径r=1,
∴PC=1+12+0−22=22,
切线长为PC2−r2=8−1=7.
故选:B.
【变式5-2】（23-24高二上·江苏盐城·期中）圆x+12+y−22=5在点1，1处切线的一般式方程为 ．
【答案】2x−y−1=0
【分析】由切线与过切点的半径垂直求得切线斜率后可得切线方程．
【详解】圆心坐标为(−1,2)，圆心与切点连线斜率为2−1−1−1=−12，所以切线的斜率为2，
切线方程为y−1=2(x−1)，即2x−y−1=0．
故答案为：2x−y−1=0．
【变式5-3】（21-22高二上·江苏盐城·期中）问题：平面直角坐标系xOy中，圆C过点A（6，0），且___________.
（在以下三个条件中任选一个，补充在横线上.）
①圆心C在直线l:2x−7y+8=0上，圆C过点B（1，5）；②圆C过点B(1,5)和D(5,−1)；③圆C过直线l:3x+5y−8=0和圆x2+y2+6y−16=0的交点.
(1)求圆C的标准方程；
(2)求过点A的圆C的切线方程.
【答案】(1)(x−3)2+(y−2)2=13
(2)3x−2y−18=0
【分析】（1）选①条件,设出圆方程，将圆心坐标代入直线方程、点的坐标代入圆方程，利用待定系数法求解；选②条件，点的坐标代入圆方程，利用待定系数法求解；选③条件，设圆C的方程为x2+y2+6y−16+λ(3x+5y−8)=0，将点A的坐标代入方程，解得λ=−2即可；
（2）求得kAC=−23，过点A的切线斜率为32，利用点斜式得答案.
【详解】（1）选①条件
设所求圆的方程为(x−a)2+(y−b)2=r2，由题意得
(6−a)2+(0−b)2=r2(1−a)2+(5−b)2=r22a−7b+8=0解得a=3，b=2，r2=13，
所以所求圆的方程是(x−3)2+(y−2)2=13.
选②条件
设圆C的方程为x2+y2+Dx+Ey+F=0，
因为圆C过点A，B，C，所以有62+02+6⋅D+0⋅E+F=012+52+1⋅D+5⋅E+F=052+(−1)2+5⋅D+(−1)2⋅E+F=0，
解得D=−6，E=−4，F=0，所以圆C的方程是x2+y2−6x−4y=0.
即(x−3)2+(y−2)2=13
选③条件
因为圆C过直线3x+5y−8=0和圆x2+y2+6y−16=0的交点，所以设圆C的方程为
x2+y2+6y−16+λ(3x+5y−8)=0，
因为圆C过点A（6，0），将点A的坐标代入方程，解得λ=−2，
所以圆C的方程是x2+y2−6x−4y=0，即(x−3)2+(y−2)2=13
（2）∵A在圆C上，kAC=−23，所以过点A的切线斜率为32，
∴过点A的切线方程是y=32(x−6)即3x−2y−18=0.
【变式5-4】（23-24高二上·江苏常州·期中）如图，已知圆O：x2+y2=1，点Pt,4为直线y=4上一点，过点P作圆O的切线，切点分别为M，N.

(1)已知t=1，求切线的方程；
(2)直线MN是否过定点?若是，求出定点坐标，若不是，请说明理由.
【答案】(1)x=1或y=158x+178
(2)直线MN恒过定点，定点坐标为0,14
【分析】（1）易知当切线斜率不存在时其方程为x=1；当切线斜率存在时设其方程为y−4=k(x−1)，两圆直线与圆位置关系建立方程，解之即可求解；
（2）如图，易知M,O,N,P四点共圆，由题意求出其圆心坐标和半径，进而可得圆的标准方程，连接MN，则MN为两圆的公共弦.利用两圆的方程相减即可求解.
【详解】（1）由题意知，当切线斜率不存在时，切线方程为x=1，满足题意；
当切线斜率存在时，设切线方程为y−4=k(x−1)，
即kx−y−k+4=0，由圆心到切线的距离等于半径，
得4−kk2+1=1，解得k=158，则切线方程为y=158x+178.
综上，切线方程为x=1或y=158x+178.
（2）连接OM、ON，则OM⊥PM,ON⊥PN，连接OP，

则M,O,N,P四点共圆，OP为圆的直径，设为圆O1，
连接MN，则MN为两圆的公共弦.
又O1(0+t2,0+42)=(t2,2)，半径为r12=(t2)2+22=t24+4，
所以O1:(x−t2)2+(y−2)2=t24+4，又O:x2+y2=1，
两圆的方程相减，得tx+4y−1=0，
即直线MN的方程为tx+4y−1=0，即t(x−0)+(4y−1)=0，
所以直线MN恒过定点(0,14).
【考点题型六】直线与圆相交弦长问题
方法总结：含参直线注意不要忽略斜率不存在的情况
【例6】（22-23高二上·江苏镇江·期中）过点0,2引直线l与圆x2+y2=2相交于A，B两点，O为坐标原点，当△AOB面积取最大值时，直线l的斜率为（ ）
A．±33B．±22
C．±1D．±3
【答案】D
【分析】当直线l的斜率不存在时，直线l即为y轴，此时A、B、O三点共线，不符合题意；当直线l的斜率存在时，设方程为y=kx+2，由S△AOB=12AOBOsin∠AOB可知当sin∠AOB=1时△AOB面积取最大值可得答案.
【详解】x2+y2=2的圆心为0,0，半径为2，
当直线l的斜率不存在时，直线点0,2可得直线l即为y轴，此时A、B、O三点共线，
不符合题意；
当直线l的斜率存在时，设方程为y=kx+2，
S△AOB=12AOBOsin∠AOB=12×2×2sin∠AOB=sin∠AOB，
所以当sin∠AOB=1即∠AOB=π2时△AOB面积取最大，
即△AOB为等腰直角三角形，可得O到l的距离为1，
即圆心0,0到直线l的距离为d=2k2+1=2k2+1=1，
解得k=±3.
故选：D.
【变式6-1】（23-24高二上·江苏常州·期中）已知直线l:mx+y+m−1=0与圆O:x2+y2=3.
(1)试判断直线l与圆O的位置关系，并说明理由；
(2)若直线l与圆O交于A,B两点，分别过A,B的圆O的切线相互垂直，求m的值.
【答案】(1)直线l与圆O相交，理由见解析
(2)m=±3−2
【分析】（1）由直线过圆内一定点P−1,1，则直线与圆相交；
（2）由直线与圆切的几何性质，得四边形OADB为正方形，转化为圆心到直线的距离为22r，从而建立关于参数m的方程求解即可.
【详解】（1）直线l与圆O相交，理由如下：
直线l可化为：mx+1+y−1=0，
由此可知l恒过定点P−1,1，
由OP=−12+12=2所以，直线l与圆C相交.
（2）设分别过A,B的圆O的切线交点为D，且切线相互垂直，
所以OA⊥AD，OB⊥BD，AD⊥BD，OA=OB=3
所以四边形OADB为正方形，
则点O到直线AB的距离为d=22r=62，
则有m−1m2+1=62，
解得：m=−2±3.

【变式6-2】（多选）（22-23高二上·江苏泰州·期中）已知圆M:(x+1)2+(y+1)2=4，直线l:x+y−2=0，P为直线l上的动点，过P点作圆M的切线PA，PB，切点为A，B，则下列说法正确的是（ ）
A．四边形MAPB面积的最小值为4
B．线段AB的最小值为22
C．当直线AB的方程为x+y=0时，∠APB最小
D．若动直线l1//l，l1且交圆M于C、D两点，且弦长CD∈(22,23)，则直线l1横截距的取值范围为(2−2,0)∪(−4,−2−2)
【答案】ABD
【分析】由切线性质PA⊥AM，PB⊥MB，PA=PB，由点到直线距离公式求得圆心M到直线l的距离，结合四边形MAPB面积计算判断AB，当AB方程为x+y=0时，由对称性求得AB，求出∠APB，然后再取一特殊值得出∠APB比此时的小可判断C，由CD弦长求出圆心到弦CD的距离的范围，从而设直线方程为x+y+m=0后可求得m的范围，从而可得横截距范围判断D．
【详解】圆M:(x+1)2+(y+1)2=4的圆心M(−1,−1)，半径为r=2，
可知|MA|=|MB|=2，PA⊥AM，|PA|=|PM|2−4，
SMAPB=2S△APM =2×12×|AM|×|PA| =2|PM|2−4，
当|PM|取最小值时，四边形MAPB面积取得最小值，
此时|PM|=|−1−1−2|12+12=22，
所以四边形MAPB面积的最小值为28−4=4，故A正确；
又圆心M(−1,−1)到直线l的距离d=|−1−1−2|12+12=22，
所以当SMAPB取得最小值时，SMAPB=12×|AB|×22，
可得|AB|=22SMAPB，故|AB|最小值22×4=22，故B正确；
当直线AB的方程为x+y=0时，kAB=−1，kOM=1，则kAB⋅kOM=−1，
所以直线AB与直线OM垂直，又O是AB中点，|MA|=|MB|=2，|OM|=2，
所以|AB|=2|MA|2−|OM|2=22，则|MA|2+|MB|2=|AB|2，
所以MA⊥MB，
易得四边形MAPB是正方形，此时∠APB=90°，而当PM=4时，直角三角形中sin∠APM=24=12，∠APM=30°，∠PB=60°<90°，故C错误；
设M到直线l1的距离为d1，因为|CD|∈(22,23)，且14|CD|2=r2−d12，
所以d12=r2−14|CD|2，则d1∈(1,2)，
设l1:x+y+m=0，所以1<|−1+(−1)+m|2<2，即2<|m−2|<2，
解得m∈(0,2−2)∪(2+2,4)，
所以直线l1的横截距−m的取值范围为(2−2,0)∪(−4,−2−2)，故D正确．
故选：ABD
【变式6-3】（23-24高二上·江苏泰州·期中）已知半径为4的圆C与直线l1：3x−4y+8=0相切，圆心C在y轴的负半轴上．
(1)求圆C的方程；
(2)已知直线l2：kx−y+3=0与圆C相交于A，B两点，当△ABC面积最大时，求直线l2的方程．
【答案】(1)x2+y+32=16；
(2)14x−2y+6=0或14x+2y−6=0.
【分析】（1）设出圆的标准方程，利用直线与圆相切即可求得圆的方程;
（2）根据几何法求弦长，表示出面积，借助基本不等式计算即可.
【详解】（1）结合题意：因为圆心C在y轴的负半轴上,且半径为4,
所以可设圆的标准方程为：x2+y−b2=16，b<0，此时圆心为0,b,
因为直线l1：3x−4y+8=0与圆相切,所以圆心0,b到直线的距离d=r=4，
即：d=−4b+832+42=4，解得：b=7（舍去），或b=−3，
所以圆C的方程为：x2+y+32=16.
（2）由上问可得：x2+y+32=16的圆心C为0,−3, r=4，
所以圆心到直线l2：kx−y+3=0的距离为：d=0+3+3k2+−12=6k2+1，
结合圆的弦长公式：AB=2r2−d2=216−d2，
直线l2与圆C相交于A，B两点，所以0所以S△ABC=12ABd=d16−d2=d216−d2≤d2+16−d22=8，
当且仅当d2=16−d2时，即d=22时，△ABC面积取到最大值8.
即d=0+3+3k2+−12=6k2+1=22，解得：k=±142，
所以直线l2的方程：14x−2y+6=0或14x+2y−6=0.
【变式6-4】（23-24高二下·江苏连云港·期中）在平面直角坐标系xOy中，已知A是圆C1:x2+(y−6)2=2上的一点，B,C是圆C2:(x−23)2+y2=4上的两点，则∠BAC的最大值为 .
【答案】π2
【分析】首先得到圆心坐标与半径，则当点A到点C2的距离最短，并且AC、AB与圆C2相切（B、C为切点）时，∠BAC取得最大值，利用锐角三角函数求出此时∠BAC2的值，即可得解.
【详解】圆C1:x2+y−62=2圆心为C10,6，半径r1=2，
圆C2:x−232+y2=4圆心为C223,0，半径r2=2，
因为A是圆C1:x2+y−62=2上的一点，B，C是圆C2:x−232+y2=4上的两点，
可知点A到点C2的距离最短，并且AC、AB与圆C2:(x−23)2+y2=4相切（B、C为切点）时，∠BAC取得最大值，
此时点A在线段C1C2与圆C1的交点，
又AC2=(23)2+(−6)2−2=22，所以sin∠BAC2=222=22，则∠BAC2=π4，
所以∠BAC=2∠BAC2=π2，所以∠BAC的最大值为π2．
故答案为：π2．
【考点题型七】圆与圆的位置关系
方法总结：判断圆与圆的位置关系的两种方法
(1)代数法:将两圆的方程组成二元二次方程组，消元化成一元二次方程，通过方程根的判别式，应用此法时要注意当∆=0或∆<0时，两圆相切或相离，均又包含两种情况，因此，应用此法比较繁琐
（2）几何法:应用此法判断圆与圆的位置关系的步骤:
①将两圆的方程化为标准方程;
②求两圆的圆心坐标和半径r1，r2;
③求两圆的圆心距d;
④比较d与|r1-r2|，|r1+r2|,的大小关系，从而判断两圆的位置关系
【例7】（23-24高二上·江苏徐州·期中）若圆C1:(x−a)2+y2=1与圆C2:x2+y2=25相交，则实数a的取值范围是（ ）
A．4,6B．4,6
C．−6,−4∪4,6D．−6,−4∪4,6
【答案】C
【分析】根据两圆相交建立不等式求解.
【详解】由圆的方程可知，C1C2=|a|，r1+r2=1+5=6,r2−r1=5−1=4，
所以根据两圆相交可得4<|a|<6，即4故选：C
【变式7-1】（23-24高二上·江苏宿迁·期中）设集合M=x,yx2+y2≤4，N=x,yx−12+y−12≤r2r>0，当M∩N=N时，r的取值范围是（ ）
A．0,2−1B．0,1
C．0,2−2D．0,2
【答案】C
【分析】根据集合的意义及集合间的运算结果可得两圆位置关系，进而可得参数范围.
【详解】由已知集合M=x,yx2+y2≤4表示以0,0为圆心，2为半径的圆M及其内部，
集合N=x,yx−12+y−12≤r2r>0表示以1,1为圆心，r为半径的圆N及其内部，
又M∩N=N，
得圆M与圆N相内切或内含，且圆N在内部，
所以MN=1−02+1−02=2≤2−r，
解得r≤2−2，
又r>0，
所以0故选：C.
【变式7-2】（23-24高二上·江苏泰州·期中）已知圆O1：x2+y2=1，圆O2：x+32+y−a2=16，如果这两个圆有公共点，则实数a取值范围是 .
【答案】−4,4
【分析】由题意确定两圆的圆心和半径，利用圆与圆的位置关系建立不等式组，解之即可.
【详解】由题意知，O1(0,0),r1=1,O2(−3,a),r2=4，则O1O2=(−3−0)2+(a−0)2=a2+9，
因为圆O1与圆O2有公共点，所以r2−r1≤O1O2≤r2+r1，即3≤a2+9≤5，
解得−4≤a≤4，所以实数a取值范围是−4,4.
故答案为：−4,4.
【变式7-3】（23-24高二上·江苏泰州·期中）已知圆C1：x2+y2−2x−6y=0，圆C2：x2+y2+mx+ny=0，若圆C2平分圆C1的周长，则m+3n=（ ）
A．20B．－20
C．10D．－10
【答案】B
【分析】求出两圆的相交弦所在直线的方程，将圆C1的圆心坐标代入相交弦所在直线的方程，即可判断结果.
【详解】圆C1：x2+y2−2x−6y=0⇒x−12+y−32=10，
所以圆心为1,3，半径为10，
若圆C2平分圆C1的周长，则圆C1的圆心1,3在圆C2与圆C1的公共弦上，
将圆C2：x2+y2+mx+ny=0与圆C1：x2+y2−2x−6y=0作差，
得两圆公共弦所在直线方程m+2x+n+6y=0，
代入1,3得m+2×1+n+6×3=0⇒m+3n=−20.
故选：B
【变式7-4】（23-24高二上·江苏常州·期中）已知圆C:x2+y2−4x−8y+12=0，A(−2,0)，O为坐标原点.
(1)若P为圆C上的动点，当∠PAO最大时，求直线PA的斜率；
(2)若圆M过点O及点A，且与圆C外切，求圆M的方程.
【答案】(1)2+3
(2)x+12+y−12=2
【分析】（1）求出点P的位置，即可得出直线PA的斜率；
（2）设出点M坐标，利用圆M与圆C外切和圆M到原点的距离即可得出圆M的方程.
【详解】（1）在圆C:x2+y2−4x−8y+12=0中，A(−2,0)
C:x−22+y−42=8，圆心C2,4，半径R=22，
当∠PAO最大时，PA与圆相切，CP⊥PA,
此时A−2,0,C2,4,B0,2点B为AC的中点，
P点恰好是以B0,2为圆心，AC=42为直径的圆B:x2+y−22=8与C:x−22+y−42=8的交点，
此时∠APC=90°,AB=BC=CP=BP=22,
∴∠PAC=30°,∠PAO=∠PAC+∠BAO=75°,
tan75°=tan30°+tan45°1−tan30°tan45°=33+11−33×1=3+2
（2）由题意及（1）得，
在圆C:x−22+y−42=8中，A(−2,0)
圆心C2,4，半径R=22，
圆M过点O及点A，
∴圆M的圆心N在直线x=-1上，
设M(−1,b)，半径为r，
因为圆M与圆C外切，
所以|CM|=(2−(−1))2+(4−b)2=r+22，即9+(4−b)2=(r+22)2，
又OM=(−1)2+b2=r，即1+b2=r2，
∴联立解得：b=1或b=7(舍)，
所以r=2，
故所求圆M的标准方程为：x+12+y−12=2.
【考点题型八】圆的公切线与相交弦
方法总结：两圆的公切线有如图所示的五种情况：
1.外离时，有4条公切线，分别是2条外公切线，2条内公切线；
2.外切时，有3条公切线，分别是2条外公切线，1条内公切线；
3.相交时，有2条公切线，都是外公切线；
4.内切时，有1条公切线；
5.内含时，无公切线.
【例8】（23-24高二上·江苏无锡·期中）若圆x2+y2=1与圆x−42+y−a2=16有3条公切线，则a=（ ）
A．−3B．3
C．3或−3D．5
【答案】C
【分析】分析可知两圆外切，可得出关于实数a的等式，解之即可.
【详解】圆x2+y2=1的圆心为C10,0，半径为r1=1，
圆x−42+y−a2=16的圆心为C24,a，半径为r2=4，
因为两圆有3条公切线，则两圆外切，则C1C2=r1+r2，即4−02+a−02=5，
解得a=±3.
故选：C.
【变式8-1】（多选）（23-24高二上·江苏宿迁·期中）若圆C1:x2+y2−4x−32=0与圆C2:(x+2)2+(y+3)2=m有且仅有一条公切线，则m的值可能为（ ）
A．1B．121
C．36D．126
【答案】AB
【分析】由C1与圆C2相内切，结合圆与圆的位置关系，求解即可.
【详解】由圆C1:x2+y2−4x−32=0与圆C2:(x+2)2+(y+3)2=m，
则圆C1:x−22+y2=36，
可得C1(2,0),C2(−2,−3)，且r1=6,r2=m，则C1C2=2+22+32=5，
若圆C1与圆C2有且仅有一条公切线，则C1与圆C2内切，
则满足C1C2=r2−r1，即m−6=5，解得m=121或m=1，
故选：AB.
【变式8-2】（23-24高二上·江苏无锡·期中）已知过点A1,3的圆C:x−a2+y−b2=r20(1)求圆C的标准方程；
(2)求过点1,0且被圆C截得的弦长为3的直线l的斜率k.
【答案】(1)x−12+y−22=1
(2)k=±15
【分析】（1）由已知条件，利用待定系数法解得a,b,r，即可求解；
（2）设直线方程为y=kx−1，求出圆心到直线的距离，再利用点到直线的距离公式求解即可.
【详解】（1）因为圆C过点A1,3，所以1−a2+3−b2=r2①，
因为圆C的圆心在直线y=2x上，所以b=2a②，
又因为圆C与直线3x−4y=0相切，所以3a−4b32+42=r③，
又0所以圆C的标准方程为x−12+y−22=1.
（2）由题意可得圆心到直线l的距离d=12−322=12，
设直线l方程为y=kx−1，即kx−y−k=0，
所以d=k−2−kk2+1=12，解得k=±15.
【变式8-3】（23-24高二上·江苏宿迁·期中）已知圆C的圆心在直线y=x上，且过点3,0,2,−1
(1)求圆C的方程；
(2)已知直线l经过0,3，并且被圆C截得的弦长为2，求直线l的方程．
【答案】(1)(x−1)2+(y−1)2=5
(2)y=3或4x−3y+9=0
【分析】（1）由点C在直线y=x上，可设出圆心坐标，利用圆上两点列出方程，求出圆心坐标即得方程；
（2）首先结合图形判断点D0,3在圆上，设出直线l，利用垂径定理将弦长问题转化为圆心到直线的距离问题求得k，即得直线方程.
【详解】（1）设圆心坐标为C(m,m)，因圆C过点A(3,0),B(2,−1),故有|CA|=|CB|,即：(m−3)2+m2=(m−2)2+(m+1)2，
解得：m=1，则C(1,1),圆的半径为5，故圆C的方程为：(x−1)2+(y−1)2=5.
（2）
如图，直线l经过的点D0,3恰好在圆C上，因直线l被圆C截得的弦长为2，故其斜率一定存在，设直线l为l:y−3=kx，
即l:kx−y+3=0，过点C作CH⊥DE,垂足为H，则HE=1,又|CE|=5,故得：CH=2,
即点C到直线l的距离为|k+2|k2+1=2，解得：k=0或k=43，即直线l的方程为：y=3或4x−3y+9=0.
【变式8-4】（23-24高二上·江苏南通·期中）在下列所给的两个条件中任选一个，补充在下面的问题中，并加以解答.
①与直线3x+4y+2=0平行；②过点5,−5；
问题：已知直线l过点P1,−2，且______.
(1)求直线l的一般式方程；
(2)若直线l与圆x2+y2=5相交于点P，Q，求弦PQ的长.
【答案】(1)3x+4y+5=0
(2)4
【分析】（1）若选①，由题可得直线l斜率，结合直线l过点P1,−2可得答案；若选②，由两点式可确定直线方程；
（2）由（1）可得直线到圆x2+y2=5圆心距离d，则弦PQ长度l满足l=2r2−d2，即可得答案.
【详解】（1）若选①，因为直线3x+4y+2=0的斜率为−34，直线l与直线3x+4y+2=0平行，
所以直线l的斜率为k=−34依题意，直线l的方程为y+2=−34x−1，即3x+4y+5=0；
若选②，因为直线l过点5,−5及1,−2，所以直线l的方程为x−51−5=y+5−2+5，即3x+4y+5=0；
（2）若选①，x2+y2=5的圆心0,0到直线3x+4y+5=0的距离为：
d=532+42=1又圆x2+y2=5的半径为r=5，所以PQ=2r2−d2=4；
若选②，圆x2+y2=5的圆心0,0到直线3x+4y+5=0的距离为：
d=532+42=1，又圆x2+y2=5的半径为r=5，所以PQ=2r2−d2=4.
【考点题型九】与圆相关的最值问题
【例9】（21-22高二下·江苏南通·期中）已知直线l：x－my＋4m－3＝0（m∈R），点P在圆x2+y2=1上，则点P到直线l的距离的最大值为（ ）
A．3B．4
C．5D．6
【答案】D
【分析】先求得直线过的定点的坐标，再由圆心到定点的距离加半径求解.
【详解】解：直线l：x－my＋4m－3＝0（m∈R）即为x−3+4−ym=0，
所以直线过定点Q3,4，
所以点P到直线l的距离的最大值为OQ+r=32+42+1=6，
故选：D
【变式9-1】（23-24高二上·江苏常州·期中）已知点P为圆A:(x−4)2+y2=4上的一个动点，点Q为圆B:(x−6)2+(y−4)2=1上的一个动点，O为坐标原点，则|PO|+|PQ|+|PB|的最小值为（ ）
A．6B．7
C．8D．9
【答案】D
【分析】取点C(3,0)，则PO=2PC，将PO+PQ+PB的最小值转化为BC距离，即可得到所求.
【详解】由题意可知：圆A的圆心A4,0，半径为r1=2，圆B的圆心B6,4，半径为r2=1，
P为圆A:(x−4)2+y2=4上一动点，Q为圆B:(x−6)2+(y−4)2=1上一动点，
O为坐标原点，
取C(3,0)，由ACAP=APAO=12，可得△ACP∼△APO，则PO=2PC，
因为PQ≥PB−1，当且仅当Q在线段PB上时，等号成立，
可得PO+PQ+PB≥PO+2PB−1
=2PC+2PB−1≥2BC−1=9，
当且仅当P在线段BC上时，等号成立，
综上所述：PO+PQ+PB≥9，当且仅当P,Q在线段BC上时，等号成立.
故选：D.

【变式9-2】（23-24高二上·江苏盐城·期中）已知点P是直线l:4x+3y+7=0上的动点，过点P引圆C:x−2+y2=r2r>0的两条切线PM，PN，M，N为切点，则PM的最小值为5时，r的值为（ ）
A．1B．2
C．3D．2
【答案】B
【分析】当PC⊥l时PC最小，PM最小，求出PC最小值即得r的值.
【详解】由题得PM2=PC2−r2，当PC⊥l时，PC最小时，PM最小.
由题得PCmin=d=|4×2+3×0+7|32+42=3，
所以52=32−r2,∴r=2.
故选：B.
【变式9-3】（多选）（23-24高二上·江苏常州·期中）圆C1:x2+y2−4x−5=0与圆C2:x2+y2−2y−3=0相交于A、B两点，则（ ）
A．AB的直线方程为2x−y+1=0
B．公共弦AB的长为2
C．线段AB的垂直平分线方程为x+2y+2=0
D．圆C1上的点与圆C2上的点的最大距离为5+5
【答案】AD
【分析】将两圆方程作差，可得出直线AB的方程，可判断A选项；求出直线AB截圆C1所得弦长，可判断B选项；分析可知，线段AB的垂直平分线为直线C1C2，求出直线C1C2的方程，可判断C选项；利用圆的几何性质可判断D选项.
【详解】对于A选项，将两圆方程作差可得−4x+2y−2=0，即2x−y+1=0，
所以，直线AB的方程为2x−y+1=0，A对；
对于B选项，圆C1的标准方程为x−22+y2=9，圆心为C12,0，半径为r1=3，
圆心C1到直线AB的距离为d=4+122+−12=5，
所以，AB=2r12−d2=29−5=4，B错；
对于C选项，圆C2的标准方程为x2+y−12=4，圆心为C20,1，半径为r2=2，
连接AC1、AC2、BC1、BC2，
因为2×0−1+1=0，所以，直线AB过圆心C2，易知C2为AB的中点，
又因为AC1=BC1，所以，C1C2⊥AB，所以，C1C2垂直平分线段AB，
kC1C2=0−12−0=−12，则直线C1C2的方程为y=−12x+1，即x+2y−2=0，C错；
对于D选项，圆C1上的点与圆C2上的点的最大距离为C1C2+r1+r2=2−02+0−12+3+2=5+5，D对.
故选：AD.
【变式9-4】（23-24高二上·江苏盐城·期中）设点P是函数y=−−x2+2x+3图象上任意一点，点Q的坐标2a,a−3a∈R，当PQ取得最小值时圆C：x+a2+y−22=r2r>0上恰有2个点到直线4x−3y−10=0的距离为1，则实数r的取值范围为 .
【答案】3,5
【分析】由点Q的坐标2a,a−3a∈R，可得Q在直线l上，l方程为：x−2y−6=0，由y=−−x2+2x+3，两边平方可得轨迹为半圆，经过圆心M与l垂直的直线为：2x+y+m=0，把圆心坐标代入可得m，即可得出此直线的方程，进而得出PQ取得最小值时的Q坐标，解得a，表示出圆心到直线4x−3y−10=0的距离，根据已知，即可得出实数r的取值范围.
【详解】因为点Q的坐标2a,a−3a∈R，
可得Q在直线l上，l：x−2y−6=0，
由y=−−x2+2x+3，
两边平方得x−12+y2=4y≤0，
可得轨迹为半圆，圆心M1,0，
经过圆心M与l垂直的直线为：2x+y+m=0，
把1,0代入可得m=−2，
则此直线方程为：2x+y−2=0，
联立2x+y−2=0x−2y−6=0，解得x=2y=−2，
所以当PQ取得最小值时，Q2,−2，
所以2a=2，解得a=1，
所以圆C为x+12+y−22=r2r>0，
圆心C−1,2到直线4x−3y−10=0的距离为：
d=−4−3×2−1042+−32=4，
由圆上恰有2个点到直线4x−3y−10=0的距离为1，
则实数r的取值范围为4−1,4+1，即3,5.
故答案为：3,5
【考点题型十】轨迹方程
方法总结：求轨迹方程的常见方法
①直接法:将动点满足的(与斜率、距离、数量积等有关的，或由平面几何知识推出的)等量关系，直接坐标化，即可得到动点轨迹方程
②定义法:若动点轨迹的条件符合某一基本轨迹的定义(如直线、圆、椭圆、双曲线、抛物线等)，可根据定义直接求，又称几何法，利用平面几何知识转化是关键.
③代入法:若动点P(x,y)依赖于另一动点Q(x0，y0)的变化而变化，并且Q(x0，y0)又在某已知(或容易先确定的)曲线上，则可先用x，y的代数式表示x0，y0，再将x0，y0代入已知曲线即可得到要求的轨迹方程，又称相关点法或转移法.
【例10】（23-24高二上·江苏盐城·期中）已知坐标平面上点Mx,y与两个定点A4,0，B1,0的距离之比等于2.
(1)求点M的轨迹方程，并说明轨迹是什么图形；
(2)记（1）中的轨迹为C，过点M1,12的直线l被C所截得的线段的长为23，求直线l的方程.
【答案】(1)点M点轨迹方程为x2+y2=4，其轨迹为以原点为圆心，2 为半径的圆
(2)x=1或3x+4y−5=0
【分析】（1）根据题意直接列方程化简求解即可，
（2）分直线l斜率不存在和直线l的斜率存在两种情况，结弦长，圆心距和半径的关系可求得结果．
【详解】（1）由题意可知，y2+(x−4)2y2+(x−1)2=2，整理，得x2+y2=4，
故点M点轨迹方程为x2+y2=4，其轨迹为以原点为圆心，2为半径的圆．
（2）由题意可知
①当直线l斜率不存在时，此时直线l的方程为x=1，满足弦长为23．
②当直线l的斜率存在时，不妨设为k，
则直线方程为y−12=k(x−1)，即kx−y−k+12=0，
则圆心(0,0)到直线l的距离为d=|−k+12|k2+(−1)2，
因为直线l被C所截得的线段的长为23，
所以d2+(3)2=22，所以d=|−k+12|k2+(−1)2=1，解得k=−34，
所以直线方程为3x+4y−5=0．
综上，满足条件的直线l的方程为x=1或3x+4y−5=0．
【变式10-1】（22-23高二上·江苏泰州·期中）长为4的线段AB的两个端点A和B分别在x轴和y轴上滑动，线段AB的中点P的轨迹为曲线C．
(1)求曲线C的方程，并说明其形状；
(2)过点M(0,2)作两条直线分别与曲线C交于P、Q两点，若直线MP，MQ的斜率之积为−2，线段PQ的中点为D，求证：存在定点E，使得|DE|为定值，并求出此定值．
【答案】(1)x2+y2=4，是以坐标原点为圆心，2为半径的圆；
(2)证明见解析，此定值为13．
【分析】（1）利用几何法直接求出轨迹方程，进而判断出形状；（2）设直线方程为y=kx+2与x2+y2=4联立求出P−4k1+k2,2−2k21+k2，由MQ的斜率为−2k，同理求出Q8kk2+4,2k2−8k2+4.根据对称性可知，判断出PQ过F0,−23.
由直角三角形的性质判断出E0,−13为OF的中点|DE|为定值.
【详解】（1）∵OA⊥OB，P为线段AB中点，
∴|OP|=12|AB|=2，设P(x,y)，则x2+y2=2，即x2+y2=4.
则曲线C是以坐标原点为圆心，2为半径的圆；
（2）
根据题意，直线MP的斜率存在且不为0，MP设斜率为k，
则直线方程为y=kx+2代入x2+y2=4中，整理得1+k2x2+4kx=0，
故xP=−4k1+k2，yP=2−2k21+k2，即P−4k1+k2,2−2k21+k2，
因为直线MP，MQ的斜率之积为−2，所以MQ的斜率为−2k，同理：Q8kk2+4,2k2−8k2+4.
根据对称性可知，直线PQ所过定点在y轴上，
不妨令2−2k21+k2=2k2−8k2+4，得k2=2，
此时yP=yQ=−23，即PQ过F0,−23，
则kPF−kQF=k2−23k−k2−23k=0，所以PQ过定点F0,−23.
连接OD，在圆O中，由垂径定理可得：OD⊥PQ.
当D、F不重合时，即OD⊥DF，所以△ODF为直角三角形，取OF的中点E0,−13，则|DE|=12|OF|=13．
当D、F重合时，取OF的中点E0,−13，则|DE|=12|OF|=13也成立．
故存在定点E，使得|DE|为定值，此定值为13．
【变式10-2】（22-23高二上·河南南阳·期中）已知点M到点O0,0的距离与点M到点A2,0的距离之比为2．
(1)求M点的轨迹C的方程；
(2)过OA的中点且倾斜角为π4的直线l与（1）中的曲线C交于E,F两点，求△AEF的面积．
【答案】(1)x−42+y2=8；
(2)72.
【分析】（1）由题意得到MOMA=2，利用两点距离公式即可得到M点的轨迹C的方程；
（2）先由题设条件及点斜式可得直线l的方程，再由弦长公式求得EF，由点线距离公式求得A到直线l的距离，从而由三角形面积公式即可求得△AEF的面积．
【详解】（1）依题意，得MOMA=2，不妨设Mx,y，
因为O0,0，A2,0，
所以x2+y2x−22+y2=2，即x2+y2=2x−22+y2，
整理得x2−8x+8+y2=0，配方得x−42+y2=8，
所以M点的轨迹C的方程为x−42+y2=8.
（2）因为O0,0，A2,0，所以OA的中点坐标为1,0，
又因为直线l的斜率为k=tanπ4=1，所以直线l的方程为y=1×x−1，即x−y−1=0，
因为曲线C的方程为x−42+y2=8，故曲线C是圆心为C4,0，半径为r=22的圆，
所以圆心C到直线l的距离为d=4−0−11+1=32，
故EF=2r2−d2=28−92=14，
又因为点A到直线l的距离为ℎ=2−0−11+1=12，即△AEF边EF上的高为ℎ=12，
所以S△AEF=12EF⋅ℎ=12×14×12=72.
【变式10-3】（22-23高二上·江苏无锡·期中）已知圆C:(x−1)2+y2=16，直线l:x+y−5=0，P(x0，y0)是直线l上的动点，点D在圆C上运动，且点T满足DT=3TO(O为原点），记点T的轨迹为E．
(1)求曲线E的方程；
(2)过点C(1,0)且不与x轴重合的直线与曲线E交于A，B两点，问在x轴正半轴上是否存在定点N，使得x轴平分∠ANB？若存在，求出点N的坐标；若不存在，请说明理由．
【答案】(1)x−142+y2=1
(2)存在；N1912,0
【分析】（1）设T(x,y)，D(m,n)，根据相关点法可求出曲线E的方程；
（2）当直线AB⊥x轴时，x轴平分∠ANB；在直线斜率存在条件下，设出直线方程并与圆的方程联立，求得韦达定理，利用设而不求法求点N的坐标，即可得解．
【详解】（1）设T(x,y)，D(m,n)，
所以DT=x−m,y−n，TO=−x,−y，
因为DT=3TO，
所以(x−m，y−n)=3(−x，−y)，
所以x−m=−3xy−n=−3y，所以m=4xn=4y，
因为D(m,n)在圆C:(x−1)2+y2=16上运动，
所以m−12+n2=16，
所以4x−12+4y2=16，
整理得，x−142+y2=1，
所以曲线E的方程为x−142+y2=1；
（2）当直线AB⊥x轴时，x轴平分∠ANB，
当直线AB斜率存在时，设直线AB的方程为y=k(x−1)，
联立x−142+y2=1y=kx−1，化简可得1+k2x2−12+2k2x+k2−1516=0，
Δ=2k2+122−4k2+1k2−1516=74k2+4>0，
设N(t,0)，A(x1，y1)，B(x2，y2)，
x1+x2=12+2k21+k2,x1x2=k2−15161+k2，
若x轴平分∠ANB，则kAN+kBN=0，所以y1x1−t+y2x2−t=0，
又y1=k(x1−1)，y2=k(x2−1)，
所以2x1x2−(t+1)(x1+x2)+2t=0，
所以2⋅k2−15161+k2−t+112+2k21+k2+2t=0，
所以k2−89−t+113+k2+t1+k2=0，
整理得，32t−198=0，
解得t=1912，
所以当N1912,0时，能使x轴平分∠ANB．
【变式10-4】（多选）（22-23高二下·江苏镇江·期中）已知点M4,0，N0,2，动点P在⊙C：x2−14x+y2−4y+44=0上，则（ ）

A．直线MN与⊙C相交
B．线段PN的中点轨迹是一个圆
C．△PMN的面积最大值为65
D．P在运动过程中，能且只能得到4个不同的Rt△PMN
【答案】BD
【分析】求出直线MN的方程，利用圆的圆心到直线的距离判断A的正误，求线段PN的中点轨迹判断B的正误，利用圆的圆心到直线的距离，转化求解三角形的面积的最在值判断C，判断MN为直径的圆与已知圆的位置关系，结合直角三角形的定义，判断D的正误.
【详解】对于A，因为M4,0，N0,2，所以kMN=2−00−4=−12，
所以直线MN的方程y−2=−12x，即x+2y−4=0，
由x2−14x+y2−4y+44=0，得(x−7)2+(y−2)2=9，
所以圆心C(7,2)，半径为3，
所以圆心C(7,2)到直线MN的距离为d=7+4−412+22=75=755>3，
所以直线与圆相离，所以A错误，
对于B，设线段PN的中点为(m,n)，则P(2m,2n−2)，
因为点P在圆(x−7)2+(y−2)2=9上，
所以(2m−7)2+(2n−2−2)2=9，即(m−72)2+(n−2)2=94表示一个圆，
所以线段PN的中点轨迹是一个圆，所以B正确，
对于C，△PMN的面积最大值为12MN(3+d)=12×20×75+3=7+35≠65，
所以C错误，
对于D，①设与直线MN垂直且过点M4,0的直线为2x−y+m=0，
则2×4−0+m=0，得m=−8，即直线为2x−y−8=0，
因为圆心到直线2x−y−8=0的距离为14−2−85=45<3，
所以直线2x−y−8=0与圆(x−7)2+(y−2)2=9有两个交点，
所以以M为直角顶点的直角三角形有2个，
②设与直线MN垂直且过点N0,2的直线为2x−y+n=0，
则2×0−2+n=0，得n=2，即直线为2x−y+2=0，
因为圆心到直线2x−y+2=0的距离为14−2+25=145>3，
所以直线2x−y+2=0与圆(x−7)2+(y−2)2=9相离，无公共点，
所以以N0,2为直角顶点的直角三角形不存在，
③以MN为直径的圆为(x−2)2+(y−1)2=5，设圆心为D，则D(2,1)，半径为5，
所以CD=(7−2)2+(2−1)2=26，
因为3−5所以以MN为直径的圆与圆(x−7)2+(y−2)2=9相交，
所以以P为直角顶点的直角三角形有2个，
综上，P在运动过程中，能且只能得到4个不同的Rt△PMN，所以D正确，
故选：BD
位置关系
判断方法
几何法
代数法
点在圆上
│MA│＝r⇔点M在圆A上
点M(x0，y0)在圆上⇔(x0－a)2＋(y0－b)2＝r2
点在圆内
│MA│点M(x0，y0)在圆内⇔(x0－a)2＋(y0－b)2＜r2
点在圆外
│MA│>r⇔点M在圆A外
点M(x0，y0)在圆外⇔(x0－a)2＋(y0－b)2＞r2
位置关系
代数关系
点在圆上
x02＋y02＋Dx0＋Ey0＋F=0
点在圆内
x02＋y02＋Dx0＋Ey0＋F<0
点在圆外
x02＋y02＋Dx0＋Ey0＋F>0
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
判定方法
几何法：设圆心到直线的距离d＝eq \f(|Aa＋Bb＋C|,\r(A2＋B2))
d＜r
d＝r
d＞r
代数法：由
eq \b\lc\{(\a\vs4\al\c1(Ax＋By＋C＝0，,（x－a）2＋（y－b）2＝r2))
消元得到一元二次方程根的判别式Δ
Δ＞0
Δ＝0
Δ＜0
图形
位置
关系
外离
外切
相交
内切
内含
图示
d与
r1，r2的
关系
d＞
r1＋r2
d＝
r1＋r2
|r1－r2|
＜d＜
r1＋r2
d＝
|r1－r2|
(r1≠r2)
0≤d＜
|r1－r2|
(r1≠r2)
位置关系
两圆外离
两圆外切
两圆相交
两圆内切
两圆内含
图示




公切线条数
4
3
2
1
0
条件
方程表示的图形
D2＋E2－4F＞0
圆心为eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(D,2)，－\f(E,2)))，半径为r＝eq \f(1,2) eq \r(D2＋E2－4F)的圆
D2＋E2－4F=0
表示点eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(D,2)，－\f(E,2)))
D2＋E2－4F<0
不表示任何图形
位置关系
判断方法
几何法
代数法
点在圆上
│MA│＝r⇔点M在圆A上
点M(x0，y0)在圆上⇔(x0－a)2＋(y0－b)2＝r2
点在圆内
│MA│点M(x0，y0)在圆内⇔(x0－a)2＋(y0－b)2＜r2
点在圆外
│MA│>r⇔点M在圆A外
点M(x0，y0)在圆外⇔(x0－a)2＋(y0－b)2＞r2
位置关系
两圆外离
两圆外切
两圆相交
两圆内切
两圆内含
图示




公切线条数
4
3
2
1
0