14.3.2.2 公式法 初中数学人教版八年级上册课件

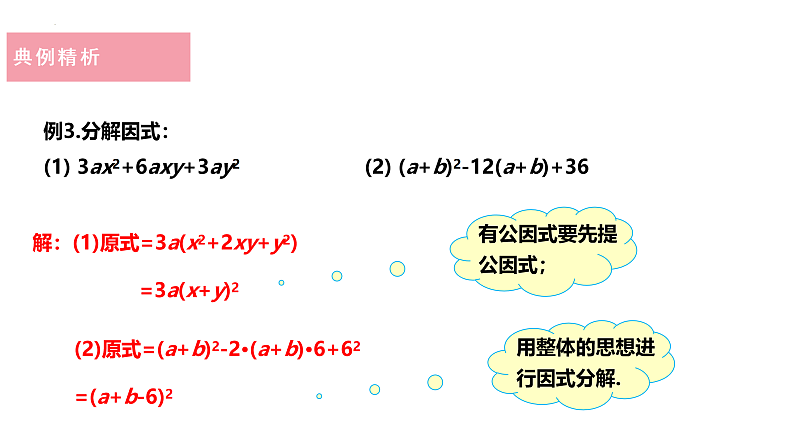
14.3.2.2公式法教学目标1.理解完全平方式及公式法的概念，会用完全平方公式进行因式分解；综合运用提公因式法和公式法对多项式进行因式分解.2.在运用公式法进行因式分解的同时，培养学生的观察、比较和判断能力以及运算能力，用不同的方法分解因式可以提高综合运用知识的能力.3.感悟知识间的相互联系，体会知识的灵活运用，从中获得成功的体验，进一步体验“整体”的思想，培养“换元”的意识.新知导入1.因式分解：把一个多项式转化为几个整式的积的形式.2.我们已经学过哪些因式分解的方法？1.提公因式法2.平方差公式：a2-b2=(a+b)(a-b)新知讲解 多项式 a2+2ab+b2 与 a2-2ab+b2 有什么特点？你能将它们分解因式吗？（1）每个多项式有几项？（3）中间项和第一项、第三项有什么关系？（2）每个多项式的第一项和第三项有什么特征？这两项都是数或式的平方，并且符号相同中间项是第一项和第三项底数的积的±2倍三项新知讲解完全平方式的特点：完全平方式:1.必须是三项式(或可以看成三项的)；2.有两个同号的数或式的平方；3.中间有两底数之积的±2倍.  凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.归纳总结+b2±=(a ± b)²a2首2+尾2±2×首×尾(首±尾)2两个数的平方和加上(或减去)这两个数的积的2倍，等于这两个数的和(或差)的平方.典例精析例2.分解因式：(1) 16x2+24x+9 (2) -x2+4xy-4y216x2+24 x+9= (4x)2 + 2·4 x·3 + 32 a2 +2 · a ·b + b2解：(1)原式=(4 x)2+2·4 x·3+32=(4x+3)2(2)原式=-(x2-4xy+4y2) =-[(x2-2·x·2y+(2y)2] =-(x-2y)2典例精析例3.分解因式：(1) 3ax2+6axy+3ay2 (2) (a+b)2-12(a+b)+36解：(1)原式=3a(x2+2xy+y2) =3a(x+y)2(2)原式=(a+b)2-2·(a+b)·6+62=(a+b-6)2归纳总结把整式乘法的平方差公式：(a+b)(a-b)=a2-b2和完全平方公式：(a+b)2=a2+2ab+b2，(a-b)2=a2-2ab+b2的等号两边互换位置，就可以得到用于分解因式的公式：a2-b2=(a+b)(a-b)，a2+2ab+b2=(a+b)2，a2-2ab+b2=(a-b)2 ，用来把某些具有特殊形式的多项式分解因式，这种分解因式的方法叫做公式法.课堂练习【知识技能类作业】必做题：1.运用公式a2+2ab+b2=(a+b)2直接对整式4x2+4x+1进行因式分解,公式中的a可以是 (　　)A.2x2 B.4x2 C.2x D.4x2. 若x2-(a+1)x+36=(x+6)2,则a的值为 (　　)A.-13 B.-11或13 C.11或-13 D.11CA课堂练习【知识技能类作业】必做题：3.分解因式:(1)-x2-4y2+4xy; (2)(x-1)2+2(x-5).解：(1)原式=-(x2-4xy+4y2) =-(x-2y)2.(2)原式=x2-2x+1+2x-10 =x2-9 =(x+3)(x-3).课堂练习【知识技能类作业】选做题：4.若n为正整数，则代数式（n＋1）（n＋2）（n2＋3n）＋1的值一定是某个正整数的平方，这个正整数为___________．（用含n的代数式表示） 5.已知：a，b，c是等腰三角形ABC的三条边，其中a，b满足a2+b2﹣2a﹣8b+17＝0，则△ABC的周长为_____． 9n2＋3n＋1课堂练习【综合拓展类作业】 课堂练习【综合拓展类作业】 课堂总结完全平方公式分解因式公式a2±2ab+b2=(a±b)2特点（1）要求多项式有三项.（2）其中两项同号，且都可以写成某数或式的平方，另一项则是这两数或式的乘积的2倍，符号可正可负.板书设计1．完全平方公式的两个特点：（1）多项式有三项；（2）其中两项同号，且都可以写成某数或式的平方，另一项则是这两数或式的乘积的2倍，符号可正可负．2．因式分解的步骤是：首先提取公因式，然后考虑用公式法．3．因式分解应进行到每一个因式不能分解为止．4．用提公因式法、平方差公式、完全平方公式分解因式，并能说出提公因式在这类因式分解中的作用．作业布置【知识技能类作业】必做题：  D A D作业布置【知识技能类作业】选做题：   作业布置【综合拓展类作业】5.已知x2－4x＋y2－10y＋29＝0，求x2y2＋2xy＋1的值．＝112＝121.解：∵x2－4x＋y2－10y＋29＝0，∴(x－2)2＋(y－5)2＝0.∵(x－2)2≥0，(y－5)2≥0，∴x－2＝0，y－5＝0，∴x＝2，y＝5，∴x2y2＋2xy＋1＝(xy＋1)2