四川省广安市友实学校2024-2025学年高二上学期第一次月月考数学试题

这是一份四川省广安市友实学校2024-2025学年高二上学期第一次月月考数学试题，共8页。试卷主要包含了已知点关于轴的对称点为，则等于，1 B，已知向量，若共面，则，下列说法不正确的是等内容，欢迎下载使用。
高二年级数学试题
（考试时间：120分钟 试卷满分：150分）
第一部分（选择题共58分）
一､单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.已知点关于轴的对称点为，则等于（ ）
A. B. C.2 D.
2.从这五个数中任取两个不同的数，则这两个数都是奇数的概率是（ ）
A.0.1 B.0.2 C.0.3 D.0.6
3.在空间四边形中，分别为的中点，则（ ）
A. B. C. D.
4.已知点，若三点共线，则的值分别是（ ）
A. B. C. D.
5.已知向量，若共面，则（ ）
A.4 B.2 C.3 D.1
6.在所有棱长均为2的平行六面体中，，则的长为（ ）
A.6 B. C. D.
7.一个盒子里装有除颜色外完全相同的四个小球，其中黑球有两个，编号为1，2；红球有两个，编号为3，4.从中不放回的依次取出两个球，表示事件“取出的两球不同色”，表示事件“第一次取出的是红球”，表示事件“取出的两球同色”，则下列说法错误的是（ ）
A. B.
C.与相互独立 D.与互斥
8.一平面截正四棱锥，与棱的交点依次为，已知，则的值为（ ）
A. B. C. D.
二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9.下列说法不正确的是（ ）
A.甲､乙二人比赛，甲胜的概率为，则比赛5场，甲胜3场
B.某医院治疗一种疾病的治愈率为，前9个病人没有治愈，则第10个病人一定治愈
C.随机试验的频率与概率相等
D.用某种药物对患有胃溃疡的500名病人治疗，结果有380人有明显疗效，现有胃溃疡的病人服用此药，则估计其会有明显疗效的可能性为
10.已知向量，则下列结论正确的是（ ）
A.若，则 B.若，则
C.的最小值为 D.的最大值为4
11.布达佩斯的伊帕姆维泽蒂博物馆收藏的达芬奇方砖在正六边形上画了具有视觉效果的正方体图案，如图，把三片这样的达芬奇方砖拼成组合，把这个组合再转换成空间几何体.若图中每个正方体的棱长为1，则下列结论正确的是（ ）
A.
B.点到直线的距离是
C.
D.异面直线与所成角的正切值为4
第二部分（非选择题共92分）
三､填空题：本题共3小题，每小题5分，共15分.
12.在深圳中考体育科目中，分为必考项目和选考项目，其中男生的必考项目为在200米和1000米项目中二选一：女生的必考项目为在200米､800米项目中二选一，小明（男生）､小花（女生）（两人选择每个项目的可能性一样）所选的必考项目不同的概率是__________.
13.已知向量满足，且.则在上的投影向量的坐标为__________.
14.已知斜三棱柱中，底面是等腰直角三角形，与都成角，则异面直线与所成角的余弦值为__________.
四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.
15.（13分）已知，
（1）若共线，求实数；
（2）若向量与所成角为锐角，求实数的范围.
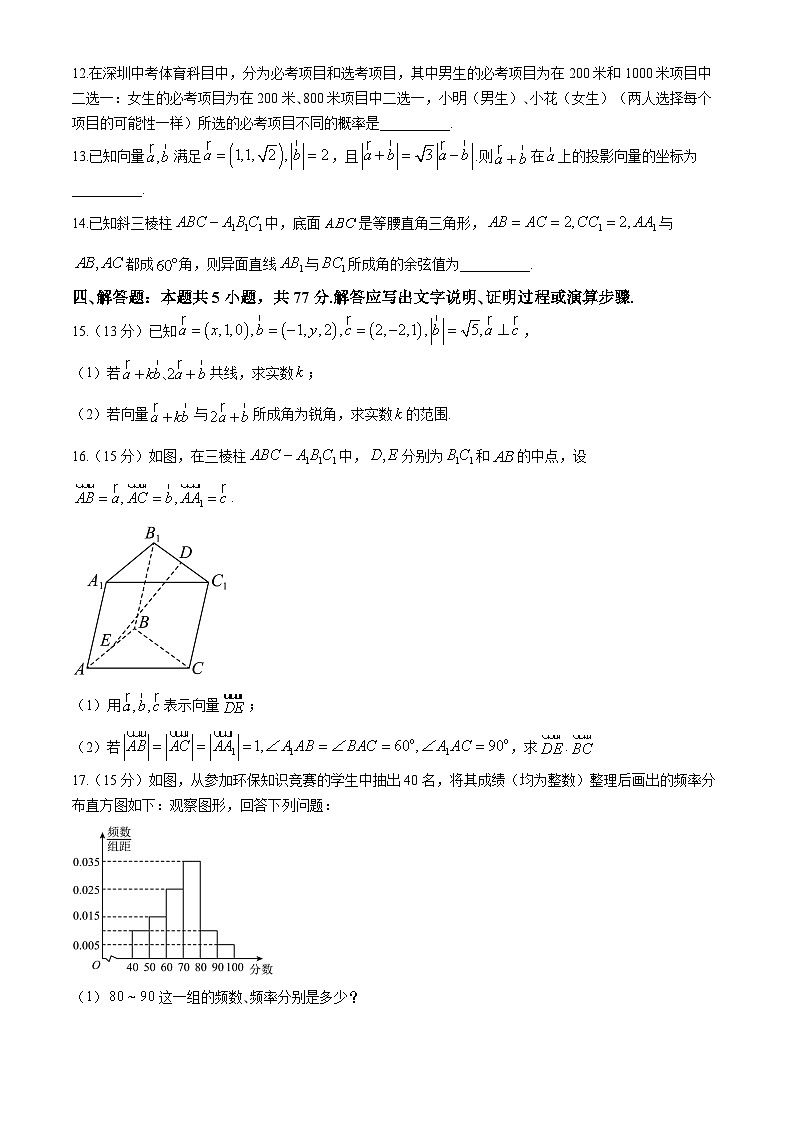
16.（15分）如图，在三棱柱中，分别为和的中点，设.
（1）用表示向量；
（2）若，求
17.（15分）如图，从参加环保知识竞赛的学生中抽出40名，将其成绩（均为整数）整理后画出的频率分布直方图如下：观察图形，回答下列问题：
（1）这一组的频数､频率分别是多少？
（2）估计这次环保知识竞赛成绩的平均数､众数､中位数.
（3）从成绩是80分以上（包括80分）的学生中选两人，求他们在同一分数段的概率.
18.（17分）甲､乙两人组成“星队”参加猜成语活动，每轮活动由甲､乙各猜一个成语，已知甲每轮猜对的概率为，乙每轮猜对的概率为在每轮活动中，甲和乙猜对与否互不影响，各轮结果也互不影响，求
（1）“星队”在两轮活动中猜对2个成语的概率；
（2）“星队”在两轮活动中猜对3个成语的概率；
（3）“星队”在两轮活动至少中猜对1个成语的概率；
19.（17分）如图，在四棱柱中，侧棱平面，为棱的中点，为棱的中点.
（1）证明：；
（2）求异面直线与所成角的余弦值；
（3）求点到平面的距离.
广安友实学校2024-2025学年度第一次月考
高二年级数学参考答案及评分标准
一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的选对一个得2分，有选错的得0分.
三､填空题：本题共3小题，每小题5分，共15分.
12. 13. 14.
三､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.
15.（13分）
解：（1）因为，
则，可得，解得
所以，所以，
因为，所以，解得.
（2）由（1）知，，
因为向量与所成角为锐角，
所以，解得，
又当时，，
所以实数的范围为.
16.（15分）
解：（1）根据题意可得；
（2）易知，且，
显然；
所以.
17.（15分）
解：（1）根据题意，的这一组的频率为，
的这一组的频率为，
的这一组的频率为，
的这一组的频率为，
的这一组的频率为，
则这一组的频率为，
其频数为；
（2）这次竞赛的平均数为，
一组的频率最大，人数最多，则众数为
70分左右两侧的频率均为0.5，则中位数为70；
（3）记“取出的2人在同一分数段”为事件，
因为之间的人数为，设为，
之间有人，设为，
从这6人中选出2人，有
､
､
，共15个基本事件，
其中事件包括，共7个基本事件，
则.
（本题第3问若用排列组合解题，正确给3分，错误给0分）
18.（17分）
解：（1）设分别表示甲乙每轮猜对成语的事件，表示第一轮甲乙猜对0个､1个､2个成语的事件，表示第二轮甲乙猜对0个､1个､2个成语的事件，表示两轮猜对0个､1个､2个､3个､4个成语的事件.
，
根据独立性的假定得：，
，
，
（1）.
（2）.
（3）.
19.（17分）
解：（1）由底面平面，得，
而，即直线两两垂直，
以点.坐标原点，直线分别为轴建立空间直角坐标系，如图，
则，
，
显然，即，所以.
（2），
所以异面直线与所成角的余弦值为.
（3），
设平面的法向量，则，令，得，
所以点到平面的距离.
（第III问可以不用向量法，答案正确同样给分）1
2
3
4
5
6
7
8
A
C
C
D
D
B
B
A
9
10
11
ABC
AC
ABC