

江苏省无锡市江阴市南闸实验学校2024-2025学年九年级上学期10月质量调研数学试题
展开
这是一份江苏省无锡市江阴市南闸实验学校2024-2025学年九年级上学期10月质量调研数学试题,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.下列方程是一元二次方程的是( )
A.3x-x2=6B.2x3-x=1C.x+=5D.2x+y=3
2.若=,则等于( )
A.B.C.D.
3.如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )
A.∠C=∠AEDB.∠B=∠D C.= D.=
4.下列说法错误的是( )
A.长度相等的两条弧是等弧 B.等边三角形都是相似三角形
C.面积相等的两个圆是等圆 D.三角形的外心到三个顶点的距离相等
5.如图,在▱ABCD中,点E在AD上,且AE=2ED,CE交对角线BD于点F,
若S△DEF=2,则S△BCF为( )
A.4B.6C.9D.18
6.如图,在Rt△ABC中,∠C=90°,AB=10.若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,则BC的长等于( )
第6题
第9题
A.5 B.5 C.5 D.6
第5题
第3题
7.若关于x的一元二次方程kx2﹣6x+9=0有实数根,则k的取值范围是( )
A.k<1B.k≤1C.k<1且k≠0D.k≤1且k≠0
8. 我国古代数学家赵爽在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法.以方程 x2+2x-35=0 即 x(x+2)=35 为例说明,记载的方法是:构造如图,大正方形的面积是(x+x+2)2.同时它又等于四个矩形的面积加上中间小正方形的面积,即 4×35+22,因此 x=5.则在下面四个构图中, 能正确说明方程 x2-5x-6=0 解法的构图是( )
9.如图,矩形ABCD中,AB=2,BC=3,以A为圆心,1为半径画圆, E是⊙A上一动点,P是BC上的一动点,则PE+PD的最小值是( )
A.2B.3 C.4 D.
第10题
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的
延长线分别交AD于点E,F,连接BD、DP,BD与CF相交于
点H,给出下列结论:①∠DPC=75°;②CF=2AE;
③;④△FPD∽△PHB;⑤AF2=EF·EB;
其中正确结论的个数是( )
A.5B.4C.3D.2
二、填空题
11.在比例尺为1:500000的江阴市地图上,若量得新建的芙蓉大道上A、B两地的距离是4cm,则A、B两地的实际距离是 km.
12.已知关于x的一元二次方程x2−8x+c=0有一个根为5,则c的值为 .
13.已知点C是线段AB的黄金分割点,且AC>BC,AB=2,则BC= .(结果保留根号)
第17题
第15题
14.如图,在△ABC中,点D、E分别在边AB、AC上,若DE∥BC,=2,DE=6cm,则BC的长为
第16题
第14题
15.如图,四边形ABCD内接于⊙O,E为BC延长线上一点.若∠DCE=65°,则∠BOD的度数是
16. 如图,原点右边7个单位有一点P,数轴上半径为1的⊙O从原点O开始以每秒2个单位的速度向右运动,经过 秒,点P在⊙O上.
17.如图,△ABC 中,AB=BC,AC=8,点 F是△ABC 的重心,BF=6,则 DF=_________.
第18题
18.如图,在Rt△ABC中,∠C=90°,两个边长为1的正方
形DEFG,GHIJ的顶点D,E,F,I,J均在△ABC的边上,
∠FGH=α(0°<α<90°),令 eq \f(S△DGJ, S△ADE) =n,当α=60°时,
n= ;当 n= eq \f(2,5) 时,S△ABC= .
三、解答题
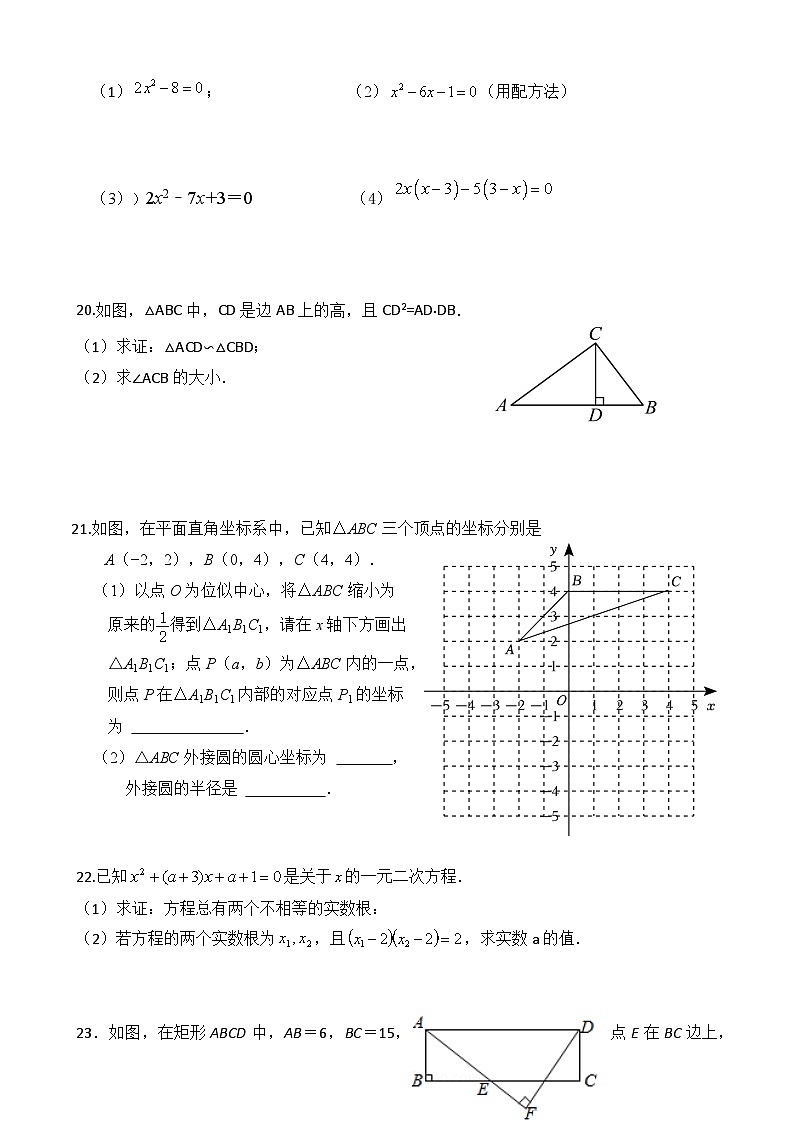
19.解方程:
(1); (2)(用配方法)
(3))2x2﹣7x+3=0 (4)
20.如图,△ABC中,CD是边AB上的高,且CD2=AD·DB.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
21.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是
A(−2,2),B(0,4),C(4,4).
以点O为位似中心,将△ABC缩小为
原来的得到△A1B1C1,请在x轴下方画出
△A1B1C1;点P(a,b)为△ABC内的一点,
则点P在△A1B1C1内部的对应点P1的坐标
为 .
△ABC外接圆的圆心坐标为 ,
外接圆的半径是 .
22.已知是关于的一元二次方程.
(1)求证:方程总有两个不相等的实数根:
(2)若方程的两个实数根为,且,求实数a的值.
23.如图,在矩形ABCD中,AB=6,BC=15,点E在BC边上,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若DF=9,求线段BE的长.
24.如图,AB是⊙O的弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=56°,求∠DEB的度数;
(2)若DC=2,AB=16,求OA的长.
25.某水果商场经销一种高档水果,原价每千克50元.
(1)连续两次降价后每千克32元,若每次下降的百分率相同.求每次下降的百分率;
(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,但商场规定每千克涨价不能超过8元,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,那么每千克应涨价多少元?
26.如图,锐角△ABC中,BC=12,BC边上的高AD=8,矩形EFGH的边GH在BC上,其余两点E、F分别在AB、AC上,且EF交AD于点K.
(1)求的值;
(2)设AK=x,矩形EFGH的面积为S.
①求S与x的函数关系式;②请直接写出S的最大值为 .
27.为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m.求旗杆高度;
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到D′处.采用同样方法,测得C′G′=1.2m,D′G′=2m.求雕塑高度(结果精确到1m).
28.如图,在矩形ABCD中,AB=5,BC=4,动点P从点B出发,以每秒2个单位长度的速度,沿射线BC方向运动,动点Q从点C出发,以每秒1个单位长度的速度,沿线段CD方向运动.点P和点Q同时出发,当点Q到达点D时,两点同时停止运动,设运动时间为t秒(t>0).
(1)用含t的代数式表示线段CP的长;
(2)当PQ与矩形的对角线平行时,求t的值;
(3)若点M为DQ的中点,求以M、P、C为顶点的三角形与△ABC相似时t的值;
(4)请直接写出点B关于直线AP的对称点B′落在△ACD内部时t的取值范围.
相关试卷
这是一份江苏省无锡市江阴市南闸实验学校2024-2025学年七年级上学期10月质量调研数学试题,共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份江苏省无锡市江阴市南闸实验学校2024-2025学年八年级上学期10月质量调研数学试题,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份江苏省无锡市江阴市南闸实验学校2023-2024学年七年级下学期3月质量调研数学试题,共4页。试卷主要包含了计算等内容,欢迎下载使用。








