甘肃省平凉市名校2025届九年级数学第一学期开学监测试题【含答案】

这是一份甘肃省平凉市名校2025届九年级数学第一学期开学监测试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，在平面直角坐标系中，四边形ABCD是菱形，点A的坐标为（0，），分别以A，B为圆心，大于AB的长为半径作弧，两弧交于点E，F，直线EF恰好经过点D，则点D的坐标为（ ）
A．（2，2）B．（2，）C．（，2）D．（+1，
2、（4分）若方程有增根，则m的值为（ ）
A．2B．4C．3D．-3
3、（4分）矩形不具备的性质是( )
A．对角线相等B．四条边一定相等
C．是轴对称图形D．是中心对称图形
4、（4分）要使式子有意义，则实数的取值范围是（ ）
A．B．C．D．
5、（4分）某次知识竞赛共有道题，每一题答对得分，答错或不答扣分，小亮得分要超过分，他至少要答对多少道题？如果设小亮答对了道题，根据题意列式得（ ）
A．B．
C．D．
6、（4分）下列函数：①y＝2x+1 ②y＝③y＝x2﹣1 ④y＝﹣8x中，是一次函数的有（ ）
A．1个B．2个C．3个D．4个
7、（4分）如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，AD＝BC，∠PEF＝25°，则∠EPF的度数是（ ）
A．100°B．120°C．130°D．150°
8、（4分）某鞋店试销一款学生运动鞋，销量情况如图所示，鞋店经理要关心哪种型号的鞋是否畅销，下列统计量最有意义的是（ ）
A．平均数B．中位数C．众数D．方差
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）若一直角三角形的两直角边长为，1，则斜边长为_____．
10、（4分）设m，n分别为一元二次方程x2+2x﹣1＝0的两个实数根，则m+n+mn＝_____．
11、（4分）已知菱形的两对角线长分别为6㎝和8㎝,则菱形的面积为______________㎝2
12、（4分）正n边形的一个外角的度数为60°，则n的值为 ．
13、（4分）如图，平行四边形 中，的平分线交于点 ， 的平分线 交于点 ，则 的长为________.
三、解答题（本大题共5个小题，共48分）
14、（12分）已知反比例函数（k为常数，k≠0）的图象经过点A（2，3）．
（1）求这个函数的解析式；
（2）判断点B（－1，6），C（3，2）是否在这个函数的图象上，并说明理由；
（3）当－3＜x＜－1时，求y的取值范围．
15、（8分）先化简，再求值：（）•，其中x=﹣1．
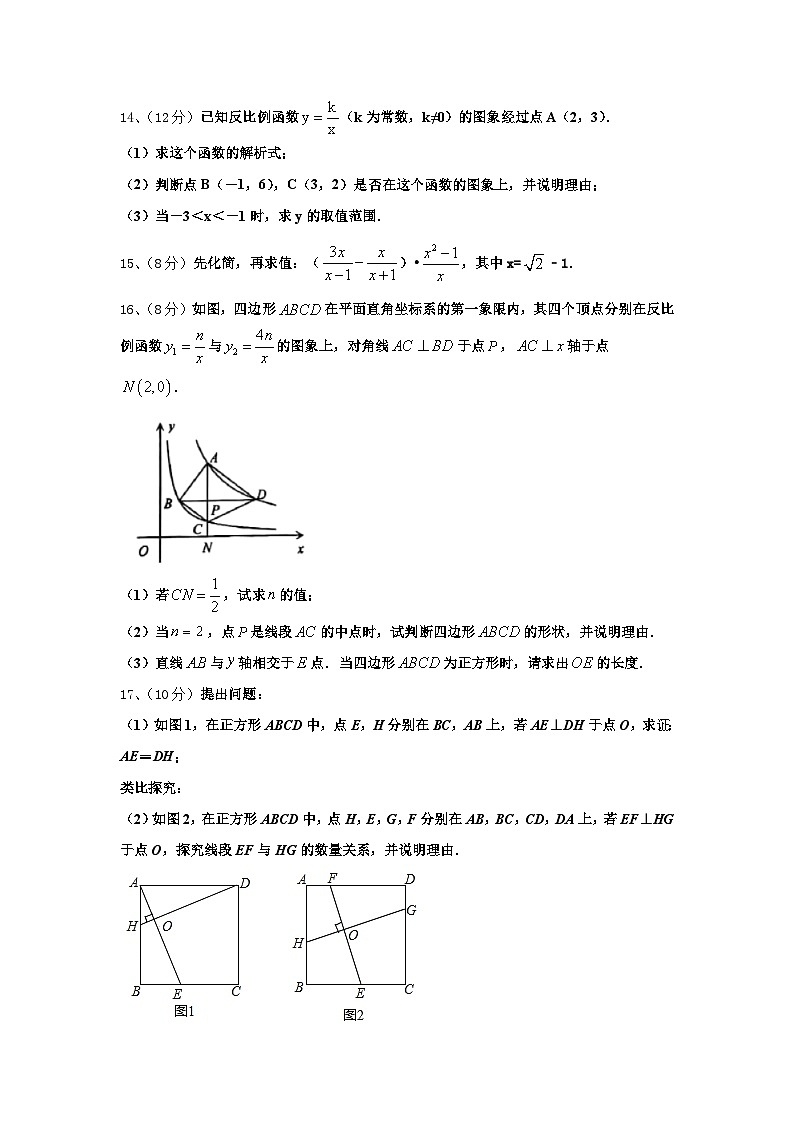
16、（8分）如图，四边形在平面直角坐标系的第一象限内，其四个顶点分别在反比例函数与的图象上，对角线于点，轴于点．
（1）若，试求的值；
（2）当，点是线段的中点时，试判断四边形的形状，并说明理由．
（3）直线与轴相交于点．当四边形为正方形时，请求出的长度．
17、（10分）提出问题：
（1）如图1，在正方形ABCD中，点E，H分别在BC，AB上，若AE⊥DH于点O，求证：AE＝DH；
类比探究：
（2）如图2，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，若EF⊥HG于点O，探究线段EF与HG的数量关系，并说明理由．
18、（10分）我们给出如下定义：把对角线互相垂直的四边形叫做“对角线垂直四边形”.
如图，在四边形中，，四边形就是“对角线垂直四边形”.
（1）下列四边形，一定是“对角线垂直四边形”的是_________.
①平行四边形 ②矩形 ③菱形 ④正方形
（2）如图，在“对角线垂直四边形”中，点、、、分别是边、、、的中点，求证：四边形是矩形.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若，，则=___________.
20、（4分）如图，正方形中，，点在边上，且．将沿对折至，延长交边于点．连结、．下列结论：①；②；③是正三角形；④的面积为1．其中正确的是______(填所有正确答案的序号)．
21、（4分）小明某学期的数学平时成绩70分，期中考试80分，期末考试85分，若计算学期总评成绩的方法如下：平时：期中：期末＝3：3：4，则小明总评成绩是________分．
22、（4分）若有意义，则x的取值范围是____．
23、（4分）若一个多边形的内角和与外角和之和是900°，则该多边形的边数是_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）为了了解全校名学生的阅读兴趣，从中随机抽查了部分同学，就“我最感兴趣的书籍”进行了调查：A．小说、B．散文、C．科普、D．其他(每个同学只能选择一项)，进行了相关统计，整理并绘制出两幅不完整的统计图，请你根据统计图提供的信息，解答下列问题：
(1)本次抽查中，样本容量为 ；
(2) ， ；
(3)扇形统计图中，其他类书籍所在扇形的圆心角是 °；
(4)请根据样本数据，估计全校有多少名学生对散文感兴趣．
25、（10分）如图，一次函数与的图象相交于
（1）求点的坐标及；
（2）若一次函数与的图象与轴分别相交于点、，求的面积.
（3）结合图象，直接写出时的取值范围.
26、（12分）如图，在平面直角坐标系中，矩形的顶点坐标为，点在边上从点运动到点，以为边作正方形，连，在点运动过程中，请探究以下问题：
（1）的面积是否改变，如果不变，求出该定值;如果改变，请说明理由;
（2）若为等腰三角形，求此时正方形的边长.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
连接DB，如图，利用基本作图得到EF垂直平分AB，则DA＝DB，再根据菱形的性质得到AD∥BC，AD＝AB，则可判断△ADB为等边三角形，所以∠DAB＝∠ABO＝60°，然后计算出AD＝2，从而得到D点坐标．
【详解】
连接DB，如图，
由作法得EF垂直平分AB，
∴DA＝DB，
∵四边形ABCD是菱形，
∴AD∥BC，AD＝AB，
∴AD＝AB＝DB，
∴△ADB为等边三角形，
∴∠DAB＝60°，
∴∠ABO＝60°，
∵A（0，），
∴OA＝，
∴OB＝OA＝1，AB＝2OB＝2，
∴AD＝AB＝2，
而AD平行x轴，
∴D（2，）．
故选：B．
考查了作图﹣基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．也考查了线段垂直平分线的性质和菱形的性质
2、D
【解析】
增根是化为整式方程后产生的不适合分式方程的根．所以应先确定增根的可能值，让最简公分母（x−1）＝0，得到x＝1，然后代入化为整式方程的方程算出m的值．
【详解】
方程两边都乘（x−1），
得x=2（x−1）-m，
∵原方程有增根，
∴最简公分母（x−1）＝0，
解得x＝1，
当x＝1时，1=2（1−1）-m
m＝-1．
故选：D．
本题考查了分式方程的增根，增根问题可按如下步骤进行：
①让最简公分母为0确定增根；
②化分式方程为整式方程；
③把增根代入整式方程即可求得相关字母的值．
3、B
【解析】
根据矩形的性质即可判断.
【详解】
解：矩形的对边相等，四条边不一定都相等，B选项错误，由矩形的性质可知选项A、C、D正确.
故选：B
本题考查了矩形的性质，准确理解并掌握矩形的性质是解题的关键.
4、C
【解析】
根据二次根式的性质，被开方数大于等于0，就可以求解．
【详解】
根据题意得：x−2⩾0，
解得x⩾2.
故选：C
此题考查二次根式有意义的条件，解题关键在于掌握其性质
5、D
【解析】
小亮答对题的得分：，小亮答错题的得分：，不等关系：小亮得分要超过分.
【详解】
根据题意，得
.
故选：.
此题主要考查了由实际问题抽象出一元一次不等式，抓住关键词语，找到不等关系是解题的关键.
6、B
【解析】
根据一次函数的定义来分析判断即可，在某一个变化过程中，设有两个变量x和y，如果满足这样的关系：y=kx+b(k为一次项系数且k≠0，b为任意常数)，那么我们就说y是x的一次函数，其中x是自变量，y是因变量 (又称函数）.
【详解】
解：①y＝2x+1是一次函数，②y＝是反比例函数，不是一次函数，③y＝x2﹣1是二次函数，不是一次函数，④y＝﹣8x是一次函数，
故选：B．
一次函数的定义是本题的考点，熟练掌握其定义是解题的关键.
7、C
【解析】
根据三角形中位线定理得到PE= AD，PF=BC，根据等腰三角形的性质、三角形内角和定理计算即可．
【详解】
解：∵P是对角线BD的中点，E，F分别是AB，CD的中点，
∴PE=AD，PF=BC，
∵AD=BC，
∴PE=PF，
∴∠PFE=∠PEF=25°，
∴∠EPF=130°，
故选：C．
本题考查三角形中位线定理，解题的关键是掌握三角形的中位线平行于第三边，并且等于第三边的一半．
8、C
【解析】
众数是一组数据中出现次数最多的数，可能不止一个，对这个鞋店的经理来说，他最关注的是数据的众数．
【详解】
对这个鞋店的经理来说，他最关注的是哪一型号的卖得最多，即是这组数据的众数．
故选：C．
此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．反映数据集中程度的平均数、中位数、众数各有局限性，因此要对统计量进行合理的选择和恰当的运用．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1
【解析】
根据勾股定理计算，得到答案．
【详解】
解：斜边长＝＝1，
故答案为：1．
本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a1+b1=c1．
10、-1
【解析】
根据一元二次方程根与系数的关系即可得出m+n＝﹣2，mn＝﹣1，将其代入m+n+mn中即可求出结论．
【详解】
∵m，n分别为一元二次方程x2+2x﹣1＝0的两个实数根，
∴m+n＝﹣2，mn＝﹣1，
则m+n+mn＝﹣2﹣1＝﹣1．
故答案为：﹣1．
本题考查了一元二次方程根与系数的关系，熟练运用一元二次方程根与系数的关系是解决问题的关键.
11、14
【解析】
根据菱形的面积等于两对角线乘积的一半求得其面积即可．
【详解】
由已知得，菱形的面积等于两对角线乘积的一半
即：6×8÷1=14cm1．
故答案为：14．
此题主要考查菱形的面积等于两条对角线的积的一半．
12、1
【解析】
解：∵正n边形的一个外角的度数为10°，
∴n=310÷10=1．
故答案为：1．
13、1
【解析】
由角的等量关系可分别得出△ABG和△DCE是等腰三角形，得出AB=AG，DC=DE，则有AG=DE，从而证得AE=DG，进而求出EG的长．
【详解】
解：∵四边形ABCD是平行四边形，
∴AD∥BC，AB=CD，
∴∠GBC=∠BGA，∠BCE=∠CED，
又∵BG平分∠ABC，CE平分∠BCD，
∴∠ABG=∠GBC，∠BCE=∠ECD，
∴∠ABG=∠AGB，∠ECD=∠CED．
∴AB=AG，CD=DE，
∴AG=DE，
∴AG-EG=DE-EG，
即AE=DG，
∵AB=5，AD=6，
∴AG=5，DG=AE=1，
∴EG=1，
故答案为1．
本题考查平行四边形的性质、等腰三角形判定等知识．由等腰三角形的判定和等量代换推出AG=DE是关键．运用平行四边形的性质和等腰三角形的知识解答．
三、解答题（本大题共5个小题，共48分）
14、（1）这个函数的解析式为：；（1）点C在函数图象上，理由见解析；（3），－2＜y＜－1．
【解析】
（1）把点A的坐标代入已知函数解析式，通过方程即可求得k的值；
（1）只要把点B、C的坐标分别代入函数解析式，横纵坐标坐标之积等于2时，即该点在函数图象上；
（3）根据反比例函数图象的增减性解答问题．
【详解】
解：（1）∵反比例函数（k为常数，k≠0）的图象经过点A（1，3），
∴把点A的坐标代入解析式，得，解得，k=2．
∴这个函数的解析式为：．
（1）∵反比例函数解析式，
∴2=xy．
分别把点B、C的坐标代入，得
（－1）×2=－2≠2，则点B不在该函数图象上；
3×1=2，则点C在函数图象上．
（3）∵k＞0，
∴当x＜0时，y随x的增大而减小．
∵当x=－3时，y=－1，当x=－1时，y=－2，
∴当－3＜x＜－1时，－2＜y＜－1．
15、1﹣2．
【解析】
先根据分式混合运算的法则把括号里的进行化简，然后进行乘法运算，再把x的值代入进行计算即可．
解：原式=
=3（x+1）﹣x+1=3x+3﹣x+1=1x+3．
当x=﹣1时，原式=1×（﹣1）﹣1=1﹣2．
16、（1）1；（2）（2）四边形ABCD为菱形，理由见解析；（3）
【解析】
（1）由点N的坐标及CN的长度可得出点C的坐标，再利用反比例函数图象上点的坐标特征可求出点n的值；
（2）利用反比例函数图象上点的坐标特征可得出点A，C的坐标，结合点P为线段AC的中点可得出点P的坐标，利用反比例函数图象上点的坐标特征可得出点B，D的坐标，结合点P的坐标可得出BP=DP，利用“对角线互相垂直平分的四边形为菱形”可证出四边形ABCD为菱形；
（3）利用正方形的性质可得出AC=BD且点P为线段AC及BD的中点，利用反比例函数图象上点的坐标特征可求出点A，C，B，D的坐标，结合AC=BD可得出关于n的方程，解之即可得出结论．
【详解】
（1）∵点N的坐标为（2，0），CN⊥x轴，且，
∴点C的坐标为（2，）．
∵点C在反比例函数的图象上，
∴n=2×=1．
（2）四边形ABCD为菱形，理由如下：
当n=2时，．
当x=2时，，
∴点C的坐标为（2，1），点A的坐标为（2，4）．
∵点P是线段AC的中点，
∴点P的坐标为（2，）．
当y=时，，
解得：，
∴点B的坐标为，点D的坐标为，
∴，
∴BP=DP．
又∵AP=CP，AC⊥BD，
∴四边形ABCD为菱形．
（3）∵四边形ABCD为正方形，
∴AC=BD，且点P为线段AC及BD的中点．
当x=2时，y1=n，y2=2n，
∴点A的坐标为（2，2n），点C的坐标为（2，n），AC=n，
∴点P的坐标为．
同理，点B的坐标为，点D的坐标为，．
∵AC=BD，
∴，
∴，
∴点A的坐标为，点B的坐标为．
设直线AB的解析式为y=kx+b（k≠0），
将A，B代入y=kx+b，得：，
解得：，
∴直线AB的解析式为y=x+．
当x=0时，y=x+，
∴点E的坐标为（0，），
∴当四边形ABCD为正方形时，OE的长度为．
本题考查了反比例函数图象上点的坐标特征、菱形的判定以及正方形的性质，解题的关键是：（1）根据点C的坐标，利用反比例函数图象上点的坐标特征求出n值；（2）利用“对角线互相垂直平分的四边形为菱形”，证出四边形ABCD为菱形；（3）利用正方形的性质及反比例函数图象上点的坐标特征，找出关于n的方程．
17、（1）见解析；（2）EF＝GH，理由见解析
【解析】
（1）由正方形的性质可得AB=DA，∠ABE=90°=∠DAH．又由∠ADO+∠OAD=90°，可证得∠HAO=∠ADO，继而证得△ABE≌△DAH，可得AE=DH；
（2）将FE平移到AM处，则AM∥EF，AM=EF，将GH平移到DN处，则DN∥GH，DN=GH．根据（1）的结论得AM=DN，所以EF=GH；
【详解】
（1）证明：∵四边形ABCD是正方形，
∴AB＝DA，∠ABE＝90°＝∠DAH．
∴∠HAO+∠OAD＝90°．
∵AE⊥DH，
∴∠ADO+∠OAD＝90°．
∴∠HAO＝∠ADO．
在△ABE和△DAH中
，
∴△ABE≌△DAH（ASA），
∴AE＝DH；
（2）解：EF＝GH．
理由：如图所示：
将FE平移到AM处，则AM∥EF，AM＝EF．
将GH平移到DN处，则DN∥GH，DN＝GH．
∵EF⊥GH，
∴AM⊥DN，
根据（1）的结论得AM＝DN，所以EF＝GH．
此题考查四边形综合题，解题关键在于证明△ABE≌△DAH，再根据平移的性质求得AM＝EF，DN＝GH.
18、（1） ③④；（2）详见解析
【解析】
（1）根据“对角线垂直四边形"的定义求解；
（2）根据三角形中位线的性质得到HG//EF，HE//GF，则可判断四边形EFGH是平行四边形，再证明∠EHG=90°，然后判断四边形EFGH是矩形；
【详解】
(1) 菱形和正方形是“对角线垂直四边形，故③④满足题意.
(2)证明：∵点分别是边、、、的中点，
∴，且；，且；.
∴.
∴四边形是平行四边形.
∵，
∴，
又∵，
∴.
∴.
∴是矩形.
本题考查了中点四边形：任意四边形各边中点的连线所组成的四边形为平行四边形，也考查了三角形中位线性质、菱形、正方形的性质.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
首先根据平方差公式进行变换，然后直接代入，即可得解.
【详解】
解：根据平方差公式，可得
=
将，，代入，得
原式==
故答案为.
此题主要考查平方差公式的运用，熟练掌握即可解题.
20、①②④
【解析】
①根据折叠的性质可以得到∠B=∠AFG=1°，AB=AF，AG=AG，根据HL定理即可证明两三角形全等；
②不妨设BG=FG=x，（x＞0），则CG=30-x，EG=10+x，在Rt△CEG中，利用勾股定理即可列方程求得；
③利用②得出的结果，结合折叠的性质求得答案即可；
④根据三角形的面积公式可得：S△FGC=S△EGC，即可求解．
【详解】
解：如图：
在正方形ABCD中，AD=AB，∠D=∠B=∠C=1°，
又∵△ADE沿AE对折至△AFE，延长EF交边BC于点G
∴∠AFG=∠AFE=∠D=1°，AF=AD，
即有∠B=∠AFG=1°，AB=AF，AG=AG，
在直角△ABG和直角△AFG中，
AB=AF，AG=AG，
∴△ABG≌△AFG；正确．
∵AB=30，点E在边CD上，且CD=3DE，
∴DE=FE=10，CE=20，
不妨设BG=FG=x，（x＞0），
则CG=30-x，EG=10+x，
在Rt△CEG中，（10+x）2=202+（30-x）2
解得x=15，于是BG=GC=15；正确．
∵BG=GF=CG，
∴△CFG是等腰三角形，
∵BG=AB，
∴∠AGB≠60°，
则∠FGC≠60°，
∴△CFG不是正三角形．错误．
∵，
∴，
∴S△FGC=S△EGC=××20×15=1．正确．
正确的结论有①②④．
故答案为：①②④．
本题考查了正方形的性质，以及图形的折叠的性质，三角形全等的证明，理解折叠的性质是关键．
21、79
【解析】
解：本学期数学总评分=70×30%+80×30%+85×40%=79(分)
故答案为79
22、x≥1．
【解析】
直接利用二次根式有意义的条件进而分析得出答案．
【详解】
∵有意义，∴x≥1，
故答案为：x≥1．
此题主要考查了二次根式有意义的条件，正确把握定义是解题关键．
23、1
【解析】
先根据已知条件以及多边形的外角和是360°，解出内角和的度数，再根据内角和度数的计算公式即可求出边数．
【详解】
解：∵多边形的内角和与外角和的总和为900°，多边形的外角和是360°，
∴多边形的内角和是900﹣360＝140°，
∴多边形的边数是：140°÷180°+2＝3+2＝1．
故答案为：1．
本题主要考查多边形的内角和定理及多边形的外角和定理，熟练掌握多边形内角和定理是解答本题的关键.n边形的内角和为：(n-2) ×180°， n边形的外角和为：360°．
二、解答题（本大题共3个小题，共30分）
24、（1）50；（2）6，15；（3）72；（4）288.
【解析】
【分析】（1）根据小说有19人占比为38%即可求得样本容量；
（2）用样本容量乘以科普的比可求得b的值，再用样本容量减去小说、科普、其他的人数即可求得a的值；
（3）用其他所占的比乘以360度即可得；
（4）用2400乘以喜欢散文类所占的比例即可得.
【详解】（1）样本容量为：19÷38%=50，
故答案为50；
（2）b=50×30%=15，
a=50-19-15-10=6，
故答案为6，15；
（3）其他类书籍所在扇形的圆心角为：=72°，
故答案为72；
（4）估计全校对散文感兴趣的学生约有：=288人.
【点睛】本题考查了条形统计图与扇形统计图的综合运用，认真识图，从图中找到必要的解题信息是解题的关键.
25、（1）；（2）9；（3）时的取值范围是．
【解析】
（1）把代入中，求得n,再代入可得m的值；
（2）分别求得B、C的坐标，以及BC的长，再利用面积公式求出答案；
（3）观察图象可直接得出结果。
【详解】
解：（1）把代入中，则
∴
把代入中，则
（2）当时，，，则点坐标为；
当时，，则点坐标为；
∴，
∴的面积；
（3）根据图象可知，时的取值范围是．
本题考查了一次函数与一元一次不等式，体现了数形结合的思想方法，准确确定出n的值，是解答本题的关键．也考查了待定系数法和三角形的面积。
26、（1）不变，；(2)正方形ADEF的边长为或或.
【解析】
(1)作交延长线于，证明，从而可得 ，继而根据三角形面积公式进行计算即可；
(2)分、、三种情况分别讨论求解即可.
【详解】
(1)作交延长线于，
∵正方形中，，，
∴，
∵，∴，
∴，
∵矩形中，，
∴，∴，
∴，
∴；
(2)①当时，作 ，
∵正方形中，，
∴，∴，
同(1)可得≌，
∴， ∴，
∴；
②当时，，
∵正方形中，，，
∴，∴≌，
∴，
∵矩形中，，
∴ ；
③当时，作，
同理得， ，
∴；
综上，正方形ADEF的边长为或或.
本题考查了矩形的性质，正方形的性质，等腰三角形的性质，全等三角形的判定与性质等，熟练掌握和灵活运用相关知识是解题的关键.注意分类讨论思想的运用.
题号
一
二
三
四
五
总分
得分
批阅人
型号
22.5
23
23.5
24
24.5
销量（双）
5
10
15
8
3