

广东省深圳市罗湖区多校2024-2025学年六年级上学期第一次月考数学试卷
展开1.画圆时,先要确定一点,这一点叫作圆的 ,一般用字母 表示,它确定了圆的 ,圆规两脚之间的距离就是圆的 ,用字母 表示,它确定了圆的 。
2.在一张长14厘米、宽10厘米的长方形纸上剪下一个最大的圆,这个圆的半径是 厘米,面积是 平方厘米.
3.如果把一个圆的直径扩大到原来的2倍,则半径会扩大到原来的 倍,周长会扩大到原来的 倍,面积会扩大到原来的 倍。
4.一个挂钟的分针长4cm,从5时到6时,分针针尖走过了 cm,分针扫过的面积是 cm2。
5.如果一个车轮滚动一周后,地面上留下的痕迹长度为1.57m,则车轮的直径是 cm。
6.“外方内圆”是我国古代建筑中常见的设计,也蕴含着为人处事的道理。如图,外面正方形的边长是10分米,那么正方形内最大圆的半径是 分米,这个圆的周长是 分米。
7.如图,把一个圆平均分成若干个小扇形,再拼成一个近似的长方形,这个长方形的长是9.42dm,宽是3dm,那么这个圆的周长是 dm,面积是 dm2。
8.如图,在长方形中的两个圆大小相等,O1、O2分别是两个圆的圆心。已知长方形的宽是4cm,这个长方形的面积是 cm2。
9.把一张周长为12.56cm的圆形纸片沿一条直径剪成两个半圆,周长增加了 cm,每个半圆的面积是 。
二、选择题。
10.井盖平面轮廓采用圆形的一个原因是圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口。这是应用了圆特征中( )
A.圆心确定圆的位置
B.半径决定圆的大小
C.同一圆内所有直径都相等
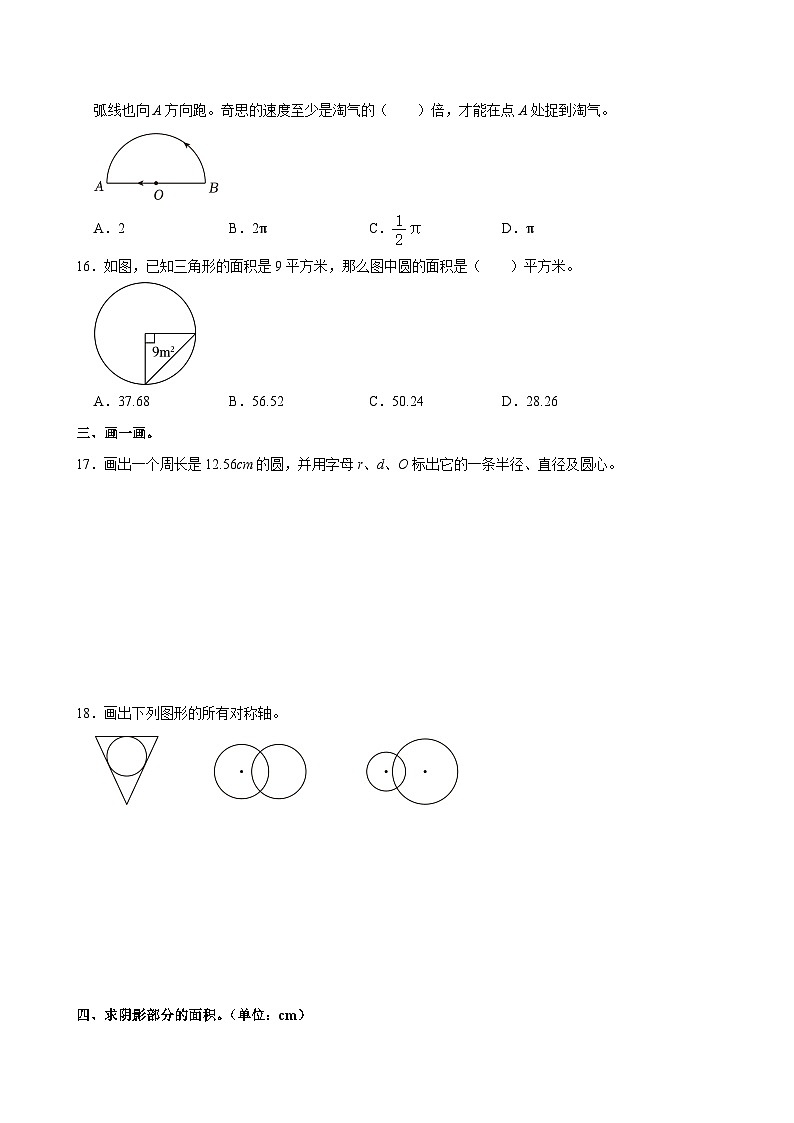
D.圆是曲边图形
11.用折一折的方法找出一张圆形纸片的圆心,至少要对折( )
A.1次B.2次C.3次D.4次
12.如图,大圆的半径和小圆的直径相等,小圆的周长是大圆周长的( )
A.B.C.D.
13.如图中,点A、B、C分别是三个半圆的圆心,并且点A、B、C和D都在同一条直线上。线段CD的长度是( )cm。
A.10B.12C.14D.16
14.如图,在两个边长相等的正方形内剪圆片,比较剩下的阴影部分,( )
A.甲剩下的多B.乙剩下的多
C.甲、乙剩下的同样多D.无法确定
15.淘气和奇思在玩“猫捉老鼠”的游戏(如图)。淘气从圆心点O向点A方向跑,奇思同时从点B点沿弧线也向A方向跑。奇思的速度至少是淘气的( )倍,才能在点A处捉到淘气。
A.2B.2πC.D.π
16.如图,已知三角形的面积是9平方米,那么图中圆的面积是( )平方米。
A.37.68B.56.52C.50.24D.28.26
三、画一画。
17.画出一个周长是12.56cm的圆,并用字母r、d、O标出它的一条半径、直径及圆心。
18.画出下列图形的所有对称轴。
四、求阴影部分的面积。(单位:cm)
19.求阴影部分的面积。(单位:cm)
20.求阴影部分的面积。(单位:cm)
五、解决问题。
21.一根铁丝可以围成一个半径为4厘米的圆,如果把这根铁丝重新围成一个正方形,这个正方形的边长是多少厘米?
22.一根20米的绳子绕一棵树干,绕了6圈,还剩1.16米,这棵树干的半径是多少米?
23.陈伯伯计划在房子后面的空地上靠墙围一个直径是8米的半圆形禽舍(如图),并从中间隔开,一边养鸡,一边养鸭。陈伯伯至少需要准备多少米的篱笆?
24.自来水公司在公园铺设自来水管道的同时,还需在路面上设置一些圆形井盖。已知一个井盖的周长是18.84分米,井盖的面积是多少平方分米?
25.用塑料绳把4个底面直径为7厘米的啤酒瓶捆扎在一起(如图),捆两圈至少需要多少厘米的绳子?(接头处用20厘米)
26.下面是一家披萨店的致歉声明。如果你是顾客,你觉得这样换有没有吃亏?请说明理由。
2024-2025学年广东省深圳市罗湖区多校六年级(上)第一次月考数学试卷
参考答案与试题解析
一、填空。
1.画圆时,先要确定一点,这一点叫作圆的 圆心 ,一般用字母 O 表示,它确定了圆的 位置 ,圆规两脚之间的距离就是圆的 半径 ,用字母 r 表示,它确定了圆的 大小 。
【解答】解:画圆时,先要确定一点,这一点叫作圆的圆心,一般用字母O表示,它确定了圆的 位置,圆规两脚之间的距离就是圆的半径,用字母r表示,它确定了圆的大小。
故答案为:圆心,O,位置,半径,r,大小。
2.在一张长14厘米、宽10厘米的长方形纸上剪下一个最大的圆,这个圆的半径是 5 厘米,面积是 78.5 平方厘米.
【解答】解:10÷2=5(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:这个圆的半径是5厘米,面积是78.5平方厘米.
故答案为:5、78.5.
3.如果把一个圆的直径扩大到原来的2倍,则半径会扩大到原来的 2 倍,周长会扩大到原来的 2 倍,面积会扩大到原来的 4 倍。
【解答】解:设原来圆的半径为r,则直径为2r,
圆的周长为:2πr,
圆的面积为:πr2,
直径扩大到原来的2倍,即半径扩大到原来的2倍,圆的半径为2r,圆的直径为4r,
圆的周长为:4πr,
圆的面积为:(2r)2π=4πr2,
则周长扩大到原来的:4πr÷2πr=2,
面积扩大到原来的:4πr2÷πr2=4。
答:半径会扩大到原来的2倍,周长扩大到原来的2倍,面积则扩大到原来的4倍。
故答案为:2,2,4。
4.一个挂钟的分针长4cm,从5时到6时,分针针尖走过了 25.12 cm,分针扫过的面积是 50.24 cm2。
【解答】解:4×2×π
=8×3.14
=25.12(cm)
42×π
=16×3.14
=50.24(cm2)
故答案为:25.12,50.24。
5.如果一个车轮滚动一周后,地面上留下的痕迹长度为1.57m,则车轮的直径是 50 cm。
【解答】解:1.57÷3.14=0.5(米)
0.5米=50厘米
答:车轮的直径是50厘米。
故答案为:50。
6.“外方内圆”是我国古代建筑中常见的设计,也蕴含着为人处事的道理。如图,外面正方形的边长是10分米,那么正方形内最大圆的半径是 5 分米,这个圆的周长是 31.4 分米。
【解答】解:最大的圆的半径是:10÷2=5(分米)圆的周长是3.14×10=31.4(分米)
答:正方形内最大圆的半径是5分米,这个圆的周长是31.4分米。
故答案为:5,31.4。
7.如图,把一个圆平均分成若干个小扇形,再拼成一个近似的长方形,这个长方形的长是9.42dm,宽是3dm,那么这个圆的周长是 18.84 dm,面积是 28.26 dm2。
【解答】解:9.42×2=18.84(dm)
3.14×32
=3.14×9
=28.26(dm2)
答:这个圆的周长是18.84dm,面积是28.26dm2。
故答案为:18.84,28.26。
8.如图,在长方形中的两个圆大小相等,O1、O2分别是两个圆的圆心。已知长方形的宽是4cm,这个长方形的面积是 24 cm2。
【解答】解:圆的半径是:
4÷2=2(厘米)
长方形的长是:
2×3=6(厘米)
长方形的面积是:
4×6=24(平方厘米)
答:长方形的面积是24平方厘米。
故答案为:24。
9.把一张周长为12.56cm的圆形纸片沿一条直径剪成两个半圆,周长增加了 8 cm,每个半圆的面积是 6.28平方厘米 。
【解答】解:直径:12.56÷3.14=4(厘米)
4+4=8(厘米)
半径:4÷2=2(厘米)
半圆面积:3.14×2×2÷2=6.28(平方厘米)
故答案为:8,6.28平方厘米。
二、选择题。
10.井盖平面轮廓采用圆形的一个原因是圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口。这是应用了圆特征中( )
A.圆心确定圆的位置
B.半径决定圆的大小
C.同一圆内所有直径都相等
D.圆是曲边图形
【解答】解:井盖平面轮廓采用圆形的原因是圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口,这里利用了同一个圆的直径都相等这一原理。
故选:C。
11.用折一折的方法找出一张圆形纸片的圆心,至少要对折( )
A.1次B.2次C.3次D.4次
【解答】解:用折一折的方法找出一张圆形纸片的圆心,至少要对折2次。
故选:B。
12.如图,大圆的半径和小圆的直径相等,小圆的周长是大圆周长的( )
A.B.C.D.
【解答】解:大圆的半径与小圆的直径相等,也就是大圆半径是小圆半径的2倍,那么小圆半径是大圆半径的,
所以小圆周长是大圆周长的。
故选:A。
13.如图中,点A、B、C分别是三个半圆的圆心,并且点A、B、C和D都在同一条直线上。线段CD的长度是( )cm。
A.10B.12C.14D.16
【解答】解:由图可知CD的长度等于AB长的3倍,
3×4=12(厘米)
答:线段CD的长度是12cm。
故选:B。
14.如图,在两个边长相等的正方形内剪圆片,比较剩下的阴影部分,( )
A.甲剩下的多B.乙剩下的多
C.甲、乙剩下的同样多D.无法确定
【解答】解:设正方形边长为4。则:
甲图:S阴影=4×4﹣(4÷2)2π=16﹣4π
乙图:S阴影=4×4﹣4×(4÷2÷2)2π=16﹣4π
即甲乙两图阴影部分面积相等。
故选:C。
15.淘气和奇思在玩“猫捉老鼠”的游戏(如图)。淘气从圆心点O向点A方向跑,奇思同时从点B点沿弧线也向A方向跑。奇思的速度至少是淘气的( )倍,才能在点A处捉到淘气。
A.2B.2πC.D.π
【解答】解:由分析可知,2πr÷2=πr
πr÷r=π
答:奇思的速度至少是淘气的π倍,才能在点A处捉到淘气。
故选:D。
16.如图,已知三角形的面积是9平方米,那么图中圆的面积是( )平方米。
A.37.68B.56.52C.50.24D.28.26
【解答】解:3.14×(9×2)
=3.14×18
=56.52(平方米)
所以图中圆的面积是56.52平方米。
故选:B。
三、画一画。
17.画出一个周长是12.56cm的圆,并用字母r、d、O标出它的一条半径、直径及圆心。
【解答】解:12.56÷3.14÷2=2(厘米)
作图如下:
18.画出下列图形的所有对称轴。
【解答】解:
四、求阴影部分的面积。(单位:cm)
19.求阴影部分的面积。(单位:cm)
【解答】解:3.14×(72﹣42)
=3.14×(49﹣16)
=3.14×33
=103.62(平方厘米)
答:阴影部分的面积是103.62平方厘米。
20.求阴影部分的面积。(单位:cm)
【解答】解:4÷2=2(厘米)
4×2﹣3.14×22÷2
=8﹣6.28
=1.72(平方厘米)
答:阴影部分的面积是1.72平方厘米。
五、解决问题。
21.一根铁丝可以围成一个半径为4厘米的圆,如果把这根铁丝重新围成一个正方形,这个正方形的边长是多少厘米?
【解答】解:3.14×2×4÷4
=6.28×4÷4
=25.12÷4
=6.28(厘米)
答:这个正方形的边长是6.28厘米。
22.一根20米的绳子绕一棵树干,绕了6圈,还剩1.16米,这棵树干的半径是多少米?
【解答】解:(20﹣1.16)÷(2×3.14)
=18.84÷6.28
=3(米)
答:这棵树干的半径是3米。
23.陈伯伯计划在房子后面的空地上靠墙围一个直径是8米的半圆形禽舍(如图),并从中间隔开,一边养鸡,一边养鸭。陈伯伯至少需要准备多少米的篱笆?
【解答】解:314×8÷2+8÷2
=12.56+4
=16.56(米)
答:陈伯伯至少需要准备16.56米的篱笆。
24.自来水公司在公园铺设自来水管道的同时,还需在路面上设置一些圆形井盖。已知一个井盖的周长是18.84分米,井盖的面积是多少平方分米?
【解答】解:18.84÷3.14÷2=3(分米)
3.14×32
=3.14×9
=28.26(平方分米)
答:井盖的面积是28.26平方分米。
25.用塑料绳把4个底面直径为7厘米的啤酒瓶捆扎在一起(如图),捆两圈至少需要多少厘米的绳子?(接头处用20厘米)
【解答】解:2×(3.14×7+7×4)+20
=2×(21.98+28)+20
=2×49.98+20
=99.96+20
=119.96(厘米)
答:捆两圈至少需要119.96厘米的绳子。
26.下面是一家披萨店的致歉声明。如果你是顾客,你觉得这样换有没有吃亏?请说明理由。
【解答】解:3.14×(20÷2)2×h=314h(立方厘米)
3.14×(10÷2)2×h×2
=3.14×25×h×2
=157h(立方厘米)
314h>157h
答:这样换吃亏了,因为体积不同。
顾客朋友们,很抱歉地通知您,因中午客流量大,店内直径20cm的披萨已经售罄,我们将为您换成相同口味的2个直径10cm披萨(厚度相同),祝您用餐愉快!
顾客朋友们,很抱歉地通知您,因中午客流量大,店内直径20cm的披萨已经售罄,我们将为您换成相同口味的2个直径10cm披萨(厚度相同),祝您用餐愉快!
广东省深圳市罗湖区多校2024-2025学年六年级上学期第一次月考数学试卷: 这是一份广东省深圳市罗湖区多校2024-2025学年六年级上学期第一次月考数学试卷,共4页。
2024-2025学年广东省深圳市罗湖区多校四年级(上)第一次月考数学试卷: 这是一份2024-2025学年广东省深圳市罗湖区多校四年级(上)第一次月考数学试卷,共8页。试卷主要包含了填一填,选一选,操作与运用,解决问题等内容,欢迎下载使用。
广东省深圳市罗湖区多校2024-2025学年四年级上学期第一次月考数学试题: 这是一份广东省深圳市罗湖区多校2024-2025学年四年级上学期第一次月考数学试题,共4页。













