广东省佛山市南海区桂城街道叠滘初级中学2024-2025学年九年级上学期10月月考数学试题

这是一份广东省佛山市南海区桂城街道叠滘初级中学2024-2025学年九年级上学期10月月考数学试题，共9页。试卷主要包含了一元二次方程配方后可化为，如图等内容，欢迎下载使用。
1．下列方程中，属于一元二次方程的是（ ）
A．B．C．D．
2．若关于x的方程的一个根是，则k的值是（ ）
A．B．2C．D．
3．一元二次方程配方后可化为（ ）
A．B．C．D．
4．如图：已知点A的坐标为，菱形ABCD的对角线交于坐标原点O，则C点的坐标是（ ）
题4图
A．B．C．D．
5．矩形具有而菱形不一定具有的性质是（ ）
A．对角相等B．对角线互相平分C．对边相等D．对角线相等
6．关于x的一元二次方程的根的情况是（ ）
A．有两个不相等的实数根B．有两个相等的实数根
C．没有实数根D．不能判断
7．如图，在中，，，于点D，E为AC的中点，，则（ ）
题7图
A．10B．8C．6D．4
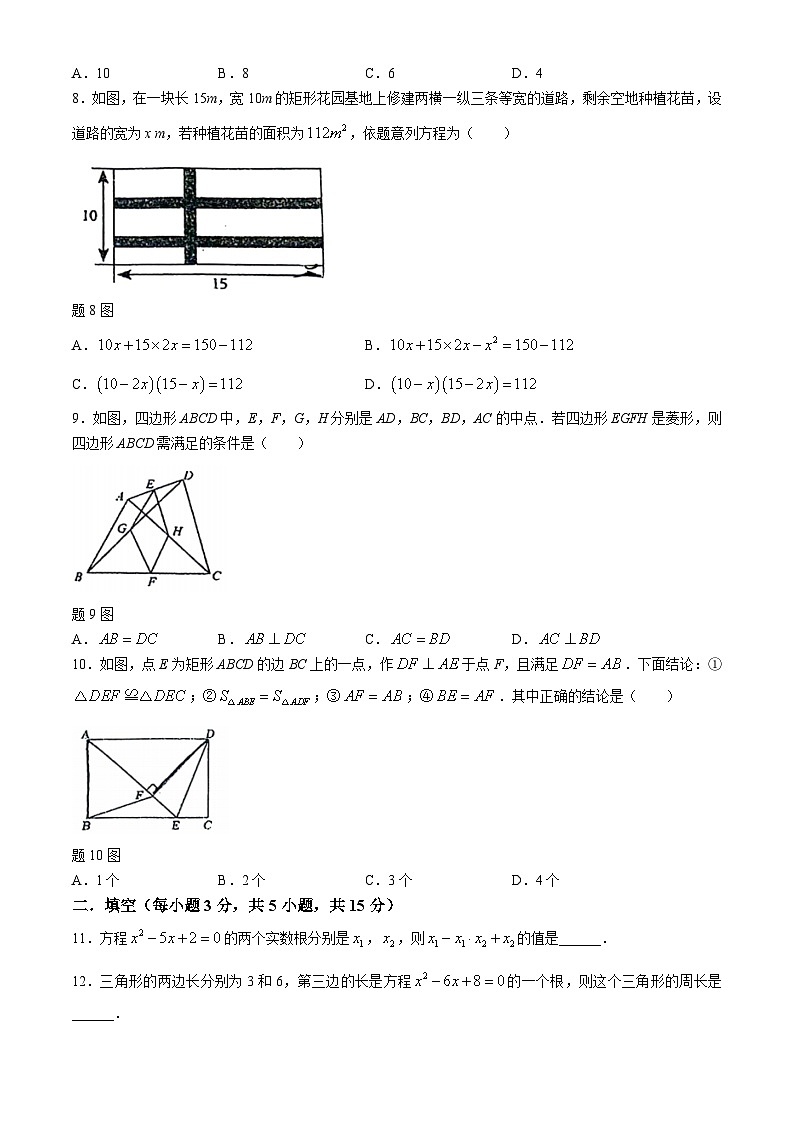
8．如图，在一块长15m，宽10m的矩形花园基地上修建两横一纵三条等宽的道路，剩余空地种植花苗，设道路的宽为x m，若种植花苗的面积为，依题意列方程为（ ）
题8图
A．B．
C．D．
9．如图，四边形ABCD中，E，F，G，H分别是AD，BC，BD，AC的中点．若四边形EGFH是菱形，则四边形ABCD需满足的条件是（ ）
题9图
A．B．C．D．
10．如图，点E为矩形ABCD的边BC上的一点，作于点F，且满足．下面结论：①；②；③；④．其中正确的结论是（ ）
题10图
A．1个B．2个C．3个D．4个
二．填空（每小题3分，共5小题，共15分）
11．方程的两个实数根分别是，，则的值是______．
12．三角形的两边长分别为3和6，第三边的长是方程的一个根，则这个三角形的周长是______．
13．如图，在菱形ABCD中，对角线AC与BD相交于点O，于点E，，，则______．
题13图
14．如图，已知四边形ABCD是矩形，，点E在AD上，．若EC平分，则BC的长为______．
题14图
15．如图，正方形ABCD的边长为2，E为AB边的中点，点F在BC边上，点B关于直线EF的对称点记为，连接，，．当点F在BC边上移动使得四边形成为正方形时，的长为______．
题15图
三．解答题一（每小翘分，共24分）
16．解方程：
（1）；
（2）．
17．若关于x的一元二次方程有一个根是，求m的值及方程的另一个根．
18．如图，菱形ABCD对角线交于点O，，，EO与AB交于点F．求证：．
四．解答题二（每小题9分，共3小题，共27分）
19．已知关于x的方程（m为实数，）．
（1）求证：此方程总有两个实数根；
（2）如果此方程的两个实数根都为正整数，求整数m的值．
20．如图，在菱形ABCD中，分别延长DC，BC至点E、F，使，，连接DB，BE，EF，FD．
（1）求证：四边形DBEF是矩形．
（2）若，，求矩形DBEF的面积．
21．某商场销售一批儿童玩具，平均每天能售出20件，每件盈利40元．经调查发现：这种玩具的售价每降低1元，平均每天能多售出2件，设每件玩具降价x元．
（1）降价后，每件玩具的利润为______元，平均每天的销售量为_______件；（用含x的式子表示）
（2）为了扩大销售，尽快减少库存，商场诀定采取降价措施，但需要每天盈利1200元，那么每件玩具应降价多少元？
五．解答题三（共2小题，每小题12分，共24分）
22．如图，在平面直角坐标系中，正方形ABCD的顶点A、B分別在y轴正半轴、x轴正半轴上，过点D作轴交x轴于点F，交对角线AC于点E．
（1）求证：；
（2）判断、的数量关系，并说明理由；
（3）若点A，B坐标分别为、，则的周长为______．
23．综合与实践：如图（1），已知点E为正方形ABCD对角线AC上一动点（不与点C重合），连接BE．
图1
（1）实践与操作：在图中，画出以点B为旋转中心，将线段BE逆时针旋转90°的线段BF，并且连接AF．
（2）观察与猜想：
观察图（1），观察并猜想AF和CE之间关系，并说明理由．
（3）探究与发现：
如图2，若点E在CA延长线上时，（2）中的两个结论是否仍然成立，说明理由．
图2
25届九年级数学上册过关练习
参考答案与试题解析
一．选择题（共10小题）
二．填空题（共5小题）
11．312．1313．14．1015．
15．详解：如图，连接，连接BD，
∵四边形ABCD是正方形，∴，BD平分，
∵E为AB边的中点，∴，
∵四边形是正方形，∴，平分，
∴点B，点，点D三点共线，∴．
三．解答题（共8小题）
16．解：（1）∵，
∴，∴，∴，
∴，；
（2）∵，∴，∴，
∴，∴，∴，．
17．解：设另一个根为，
∵，
∴，，解得，，；
∴m的值为3，方程的另一个根为1．
18．证明：∵，，∴四边形AEBO是平行四边形．
又∵菱形ABCD对角线交于点O，∴，即．
∴四边形AEBO是矩形．∴．
19．（1）证明：由题知，
因为，所以次方程为一元二次方程，
则，
因为，所以此方程总有两个实数根．
（2）解：由一元二次方程的求根公式得，，即，，又此方程的两个实数根都为正整数，且m为整数，所以或．
20．（1）证明：∵，，
∴四边形DBEF是平行四边形，∵四边形ABCD是菱形，
∴，∴，∴，
∴四边形DBEF是矩形；
（2）解：∵四边形ABCD是菱形，，，
∴，，
∴和是等边三角形，∴，，
∵四边形DBEF是矩形，
∴，∴，
∴，∴，
∴矩形DBEF的面积为：．
21．解：（1）；．
（2）依题意，得：，
整理，得：，
解得：，．
∵为了扩大销售，增加盈利，尽快减少库存，∴．
答：每件玩具应降价20元．
22．（1）证明：∵四边形ABCD是正方形，∴，，
在与中，∴，∴；
（2）解：，理由如下：
如图所示，设BC、DF交于点H，
∵轴，，∴，
又∵，∴，
∵，∴，
又∵，
∴，即，∴；
（3）解：如图所示，过点D作轴于点G，
则四边形OGDF是矩形，∵四边形ABCD是正方形，
∴，，∵，
∴，
∴，∴，，
∵点A，B坐标分别为、，
∴，，
∴，．
∵．
∴的周长为．故答案为：24．
23．解：（1）如图所示即为所求．
（2）∵四边形ABCD是正方形，
∴，，，
∵将线段BE逆时针旋转90°的线段BF，
∴，，∴，
又∵，∴，
∴，，
∴，
∴．故答案为：，；
图1
（3）（2）中的两个结论是否仍然成立，现由如下：
∵四边形ABCD是正方形，
∴，，，
∵将线段BE逆时针旋转90°的线段BF，
∴，，∴，
又∵，∴，
∴，，
∴，
∴，∴．
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
D
B
D
A
B
C
A
C