福建省宁德市古田县第一中学2024-2025学年高一上学期第一次月考数学试题

这是一份福建省宁德市古田县第一中学2024-2025学年高一上学期第一次月考数学试题，文件包含福建省宁德市古田县第一中学2024-2025学年高一上学期第一次月考数学试题docx、2024-2025第一学期高一数学月考1质量分析报告pdf、古田一中20242025学年第一学期高一月考1_数学答题卡pdf等3份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
（试卷满分：150分 考试时间：120分钟）
注意事项：
1.答卷前，考生务必将姓名､座号､考场､班级填写在答题卡上.
2.选择题用2B铅笔将答案涂在答题卡上，非选择题将答案写在答题卡上.
3.考试结束，考生只将答题卡交回，试卷自己保留.
一､单项选择题：本大题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.已知集合，集合，则（ ）
A. B. C. D.
2.命题“对任意，都有”的否定是（ ）
A.对任意，都有 B.存在，使得
C.不存在，使得 D.存在，使得
3.下列命题为真命题的是（ ）
A.若，则
B.若，则
C.若，则
D.若，则
4.“且”是“”的（ ）
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.有三个房间需要粉刷，粉刷方案要求：每个房间只用一种颜色，且三个房间颜色各不相同.已知三个房间的粉刷面积（单位：）分别为，且，三种颜色涂料的粉刷费用（单位：元）分别为，且.在不同的方案中，最低的总费用（单位：元）是（ ）
A. B.
C. D.
6.下列函数中，的最小值为4的是（ ）
A. B.
C. D.
7.定义集合的乘运算：.已知集合，集合，则集合非空真子集的个数为（ ）
A.6 B.14 C.30 D.62
8.某位同学经常会和爸爸妈妈一起去加油，经过观察他发现了一个有趣的现象：爸爸和妈妈的加油习惯是不同的.爸爸每次加油都说：“师傅，给我加250元的油”，而妈妈则说：“师傅，帮我把油箱加满”.这位同学若有所思，如果爸爸､妈妈都加油两次，两次的加油价格不同，爸爸每次都是加250元的油，妈妈每次都加满油箱，我们规定谁的平均单价低谁就合算，那么请问爸爸､妈妈谁更合算呢？（ ）
A.爸爸 B.妈妈 C.一样 D.不确定
二､多项选择题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9.已知全集为，若集合满足：，则下列关系可能成立的是（ ）
A.⫋ B.
C. D.
10.“关于不等式在上恒成立”成立的一个充分不必要条件可以是（ ）
A. B.
C. D.
11.对于分式不等式有多种解法，其中一种方法如下，将不等式等价转化为，然后将对应方程的所有根标注在数轴上，形成如图所示的五个区间，并且可得在从右向左的各个区间内的值为正､负依次相间，即可得到所求不等式的解集.
利用此法求解下列问题：已知区间的左端点为，右端点为，定义区间的长，若满足的构成的区间的长度和为2，则实数的取值可以是（ ）
A. B. C. D.1
三､填空题：本大题共3小题，每小题5分，共15分.
12.已知集合，若，则__________.
13.若命题“”为假命题，请写出一个满足条件的的值__________.
14.已知，若，则的最大值为__________.
四､解答题：本大题共5小题，共77分，解答题应写出文字说明，证明过程或演算步骤，在答题卷上相应题目的答题区域内作答.
15.（本小题13分）
已知集合，集合.
（1）若，求；
（2）若，求实数的取值范围.
16.（本小题15分）
已知：实数满足（其中：实数满足.
（1）若，且为假命题，为真命题，求实数的取值范围；
（2）若是的必要不充分条件，求实数的取值范围.
17.（本小题15分）
已知关于的不等式.
（1）若该不等式的解集为，求的值；
（2）当时，若不等式在上恒成立，求实数的取值范围；
（3）当时，求此不等式的解集.
18.（本小题17分）
如图所示是某水产养殖大网箱的平面图，四周的实线为网衣，为避免混养，用筛网（图中虚线）把大网箱隔成大小一样的8个小网箱.
（1）若大网箱的面积为108平方米，每个小网箱的长，宽设计为多少米时，才能使围成的网箱中筛网总长度最小；
（2）若大网箱的面积为160平方米，网衣的造价为112元/米，筛网的造价为96元/米，且大网箱的长与宽都不超米，则小网箱两相邻边长分别为多少米时，可使网衣和篮网的合计造价最低？
19.（本小题17分）
学习与探究问题：正实数，满足，求的最小值.求解本问题的方法很多，其中一种求解方法是：，当且仅当即且时，即时等号成立.这种解题方法叫作“1”的代换，利用上述求解方法解决下列问题：
（1）已知正实数，满足，求的最小值；
（2）若实数满足，试比较与的大小，并注明等号成立的条件；
（3）利用（2）的结论，求的最小值，并注明使得取得最小值时的值.
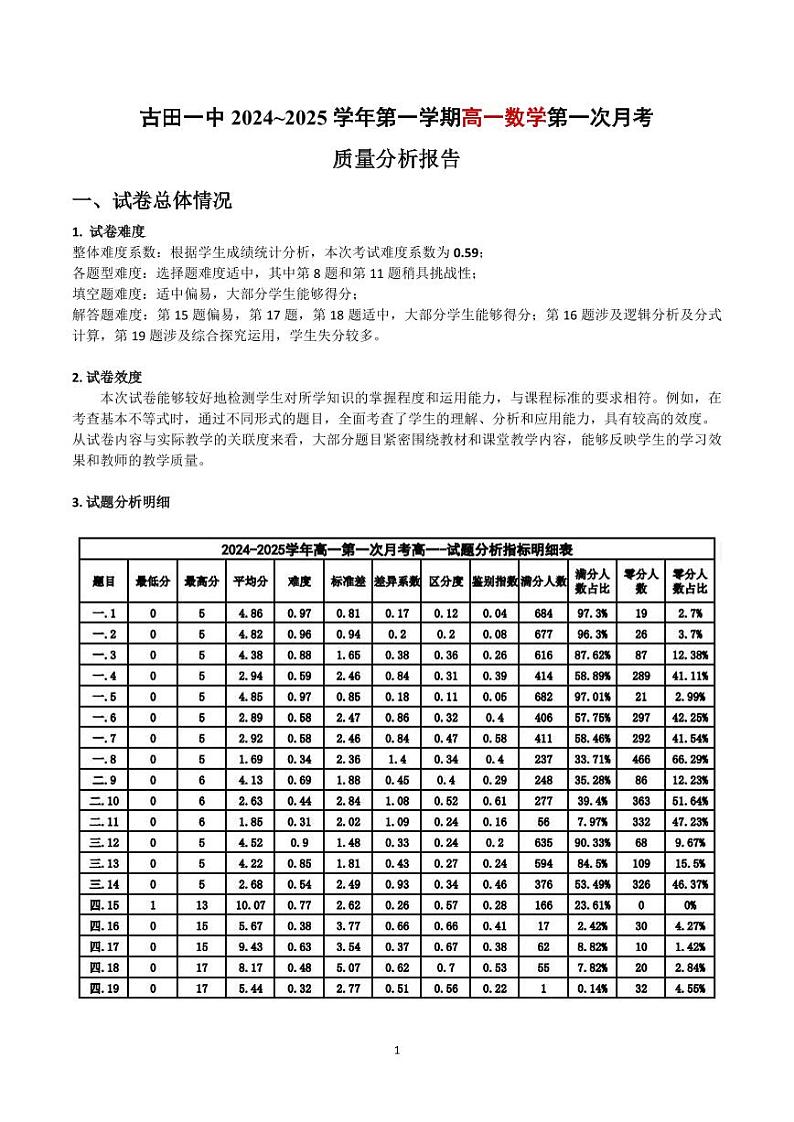
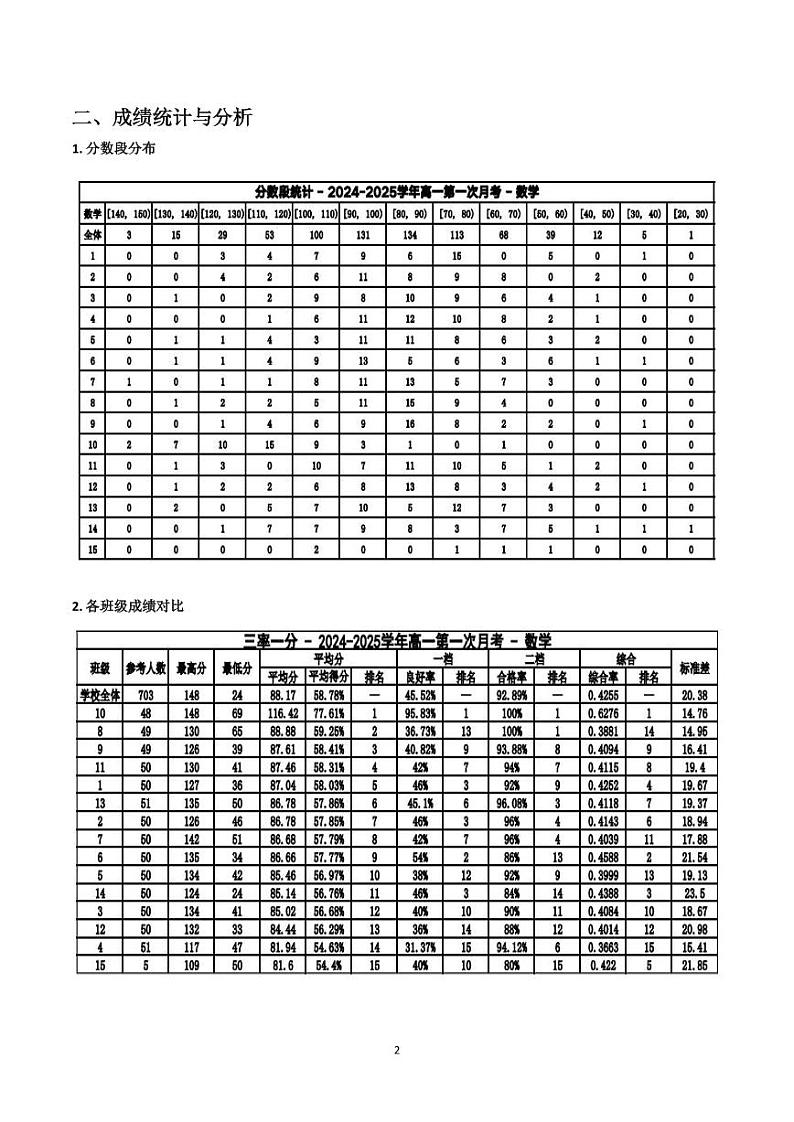
古田一中2024~2025学年第一学期高一第一次月考
数学试题参考答案及评分标准
一､单项选择题
【第5题解析】
法一：由，
所以，
故；
同理，，
故，
因为，
故.
故最低费用为.
法二：取特值，如，易得为最小值.
【第8题解析】
由题意，设第一次加油单价为元，第二次为元，油箱加满为升，
则妈妈两次加油共需付款元，爸爸两次能加升油，
设爸爸两次加油的平均单价为元/升，妈妈两次加油的平均单价为元/升，
则，且，
所以，即，
所以爸爸的加油方式更合算.
二､多项选择题
【第11题解析】
等价于，
当时满足条件的构成的区间为，长度为2，符合题意，A正确；
当时满足条件的构成的区间为，长度为1，不符合题意，B不正确；
当时满足条件的构成的区间为，长度为2，符合题意，C正确；
当时满足条件的构成的区间为，长度为2，符合题意，D正确.
故选：ACD.
三､填空题
12.
13.答案不唯一，可填：1，2，3
14.4
【第14题解析】
根据题意可得，
又
所以
，
当且仅当，即时等号成立，
所以的最大值为4.
四､解答题
15.（本小题13分）
解：（1）时，，
则
（2），
当时，，解得；
当时，，解得.
综上，实数的取值范围为
16.（本小题15分）
解：（1）时，或.
：原不等式等价于，解得
为假命题，为真命题，
，
解得
（2）设或，
是的必要不充分条件，⫋，
或，又
解得或
17.（本小题15分）
解：（1）依题的根为和2，
由韦达定理得，
解得
（2）当时，不等式可化为
结合函数的图像，可知只要在和时，即可，
则有，
解得.
（3）当时，不等式可化为
的根为
当即时，不等式为，解集为；
当即时，结合函数的图像，
不等式的解集为
当即时，结合函数的图像，
不等式的解集为
综上所述，当时，不等式的解集为；
当时，不等式的解集为；
当时，不等式的解集为
18.（本小题17分）
解：（1）依题得
设筛网总长度为米，则
当且仅当即时，篮网总长度最小
答：每个小网箱长为米，宽为3米时，围成的网箱中筛网总长度最小.
（2）法一：依题得，即
设总造价为元，则
.
由得，解得.
当且仅当即时，造价最低
答：小网箱两条相邻边长为4米和5米时，可使网衣和筛网的合计造价最低
法二：依题得，
设总造价为元，则
由得，
当且仅当且，即时，造价最低.
答：小网箱两条相邻边长为4米和5米时，可使网衣和篮网的合计造价最低.
19.（本小题17分）
解：（1）由得，
则.
当且仅当即时，.
（2）由，可得
，
又由，当且仅当时，等号成立，
所以，
所以，当且仅当且同号时等号成立，
此时满足
（3）令且，
由，即，
则，解得，
因为，所以，则，
所以，
当且仅当，即等号成立，此时，
所以当时，有最小值.1
2
3
4
5
6
7
8
D
B
C
A
B
C
D
A
9
10
11
BCD
AB
ACD