初中数学湘教版（2024）八年级下册2.6.1菱形的性质习题课件ppt

这是一份初中数学湘教版（2024）八年级下册2.6.1菱形的性质习题课件ppt，共36页。PPT课件主要包含了名师点金，知识点4菱形的面积等内容，欢迎下载使用。

1.菱形的性质：菱形具有平行四边形的一切性质.菱形的性质还有：(1)菱形的每一条对角线平分一组对角；(2)菱形的四条边相等；(3)菱形是轴对称图形；(4)菱形的对角线互相垂直.2.菱形的面积等于两条对角线乘积的一半.
知识点1　菱形的定义及其对称性
1.[2023·福建]如图，在菱形ABCD中，AB＝10，∠B＝60°，则AC的长为 　10　⁠.
由题意得到AB＝BC，又∠B＝60°，∴△ABC是等边三角形，∴AC＝AB＝10.
2.[2023·大庆]将两个完全相同的菱形按如图方式放置，若∠BAD＝α，∠CBE＝β，则β＝(　　)
∵四边形ABCD和四边形BGHF是完全相同的菱形，
∴∠DBE＝∠BAD＝α，AB＝AD，
∠ABD＝∠CBD＝∠CBE＋∠DBE，
∴∠ADB＝∠ABD＝β＋α.
∵∠BAD＋∠ADB＋∠ABD＝180°，
∴α＋β＋α＋β＋α＝180°，
知识点2　菱形边的性质
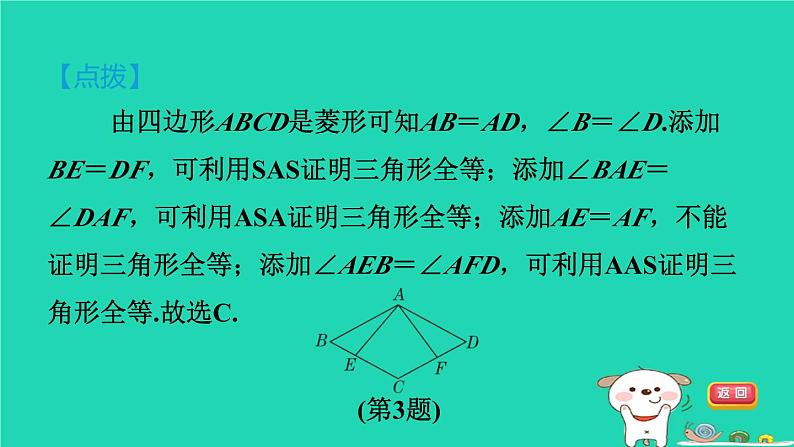
3.[2023·郴州二中模拟]如图，四边形ABCD是菱形，点E，F分别在BC，DC边上，添加以下条件不能判定△ABE≌△ADF的是(　　)
由四边形ABCD是菱形可知AB＝AD，∠B＝∠D.添加BE＝DF，可利用SAS证明三角形全等；添加∠BAE＝∠DAF，可利用ASA证明三角形全等；添加AE＝AF，不能证明三角形全等；添加∠AEB＝∠AFD，可利用AAS证明三角形全等.故选C.
4.[2022·济南]已知：如图，在菱形ABCD中，E，F是对角线AC上两点，连接DE，DF，∠ADF＝∠CDE.求证：AE＝CF.
知识点3　菱形对角线的性质
5.[2023·湘潭]如图，菱形ABCD中，连接AC，BD，若∠1＝20°，则∠2的度数为(　　)
∵四边形ABCD是菱形，
∴AB∥CD，AC⊥BD.∴∠DCA＝∠1＝20°.
∴∠2＝90°－∠DCA＝70°
6.[2023·丽水]如图，在菱形ABCD中，AB＝1，∠DAB＝60°，则AC的长为(　　)
7.[2023·乐山]如图，菱形ABCD的对角线AC与BD相交于点O，E为边BC的中点，连接OE，若AC＝6，BD＝8，则OE＝(　　)
9.[2022·淄博]如图，在边长为4的菱形ABCD中，E为AD边的中点，连接CE交对角线BD于点F，若∠DEF＝∠DFE，则这个菱形的面积为(　　)
易错点　不会利用对角线所在直线为对称轴这一性质而致错
10. [新考法 最值探究法]如图，点P是边长为1的菱形ABCD的对角线AC上的一个动点，点M，N分别是AB，BC边的中点，则MP＋PN的最小值是(　　)
如图，取AD的中点M'，连接M'N，M'P，则有MP＝M'P.所以MP＋PN的最小值为线段M'N的长，即菱形的边长.
利用菱形的边角性质求角度11.[2023·嘉兴]如图，在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，连接EF.(1)求证：AE＝AF；
(2)若∠B＝60°，求∠AEF的度数.
【解】∵四边形ABCD是菱形，∴∠B＋∠BAD＝180°.而∠B＝60°，∴∠BAD＝120°.又∵∠AEB＝90°，∠B＝60°，∴∠BAE＝30°.由(1)知△ABE≌△ADF，AE＝AF，∴∠BAE＝∠DAF＝30°.∴∠EAF＝120°－30°－30°＝60°.∴△AEF是等边三角形，∴∠AEF＝60°.
利用菱形对角线的性质求线段长12.[2023·长春]将两个完全相同的含有30°角的直角三角尺在同一平面内按如图所示位置摆放，点A，E，B，D依次在同一条直线上，连接AF，CD.
(1)求证：四边形AFDC是平行四边形；
【证明】∵△ACB≌△DFE，∴AC＝DF，∠CAB＝∠FDE，∴AC∥DF，∴四边形AFDC是平行四边形.
(2)已知BC＝6 cm，当四边形AFDC是菱形时，AD的长为 　18　⁠cm.
利用菱形的性质判断四边形的形状13.[2022·张家界]如图，菱形ABCD的对角线AC，BD相交于点O，点E是CD的中点，连接OE，过点C作CF∥BD交OE的延长线于点F，连接DF.(1)求证：△ODE≌△FCE；
(2)试判断四边形ODFC的形状，并写出证明过程.
【解】四边形ODFC为矩形.证明如下：∵△ODE≌△FCE，∴OE＝FE，又∵CE＝DE，∴四边形ODFC为平行四边形.∵四边形ABCD为菱形，∴AC⊥BD，即∠DOC＝90°，∴四边形ODFC为矩形.
利用菱形的性质探究图形的形状14. [新考法 直观判断法]如图，菱形ABCD的一个内角∠B＝60°，E为BC的中点，F为CD的中点，连接AE，AF，EF.
(1)△AEF的形状如何？请证明.
【解】△AEF为等边三角形.证明如下：连接AC，如图①所示.
∵四边形ABCD是菱形，∠B＝60°，∴AB＝BC＝CD＝AD，∠D＝∠B＝60°，∴△ABC和△ADC都是等边三角形，∴AB＝AC＝AD，∠BAC＝∠DAC＝60°.
∵E，F分别是边BC，CD的中点，∴AE平分∠BAC，AF平分∠DAC，AE⊥BC，AF⊥CD，∴∠CAE＝∠CAF＝30°，∴∠EAF＝60°.∵菱形ABCD的面积为BC·AE＝CD·AF，BC＝CD，∴AE＝AF，∴△AEF为等边三角形.
(2)若E为BC上的任意一点，F为CD上的任意一点，且∠EAF＝60°，△AEF的形状如何？请证明.
【解】△AEF为等边三角形.证明如下：连接AC，如图②所示.
由(1)得△ABC和△ADC是等边三角形，∴∠BAC＝∠ACD＝60°，AB＝AC.∵∠EAF＝60°＝∠BAC，∴∠BAE＝∠CAF.