初中数学湘教版（2024）九年级下册1.1 二次函数多媒体教学ppt课件

这是一份初中数学湘教版（2024）九年级下册1.1 二次函数多媒体教学ppt课件，共45页。PPT课件主要包含了学习目标，课时讲解，逐点导讲练，课堂小结，作业提升，课时流程，知识点，感悟新知，答案A，答案D等内容，欢迎下载使用。

二次函数 y=ax2+k 的图象(拓展点)二次函数 y=a(x－h) 2的图象二次函数 y=a(x－h) 2+k的图象与 性质二次函数 y=ax2， y=ax2+k， y=a( x－h) 2， y=a(x－h) 2+k之间的关系(拓展点)
二次函数 y=ax2+k 的图象(拓展点)
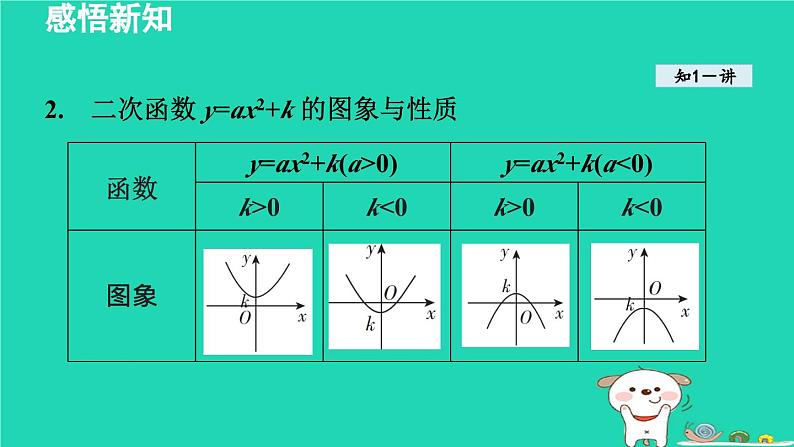
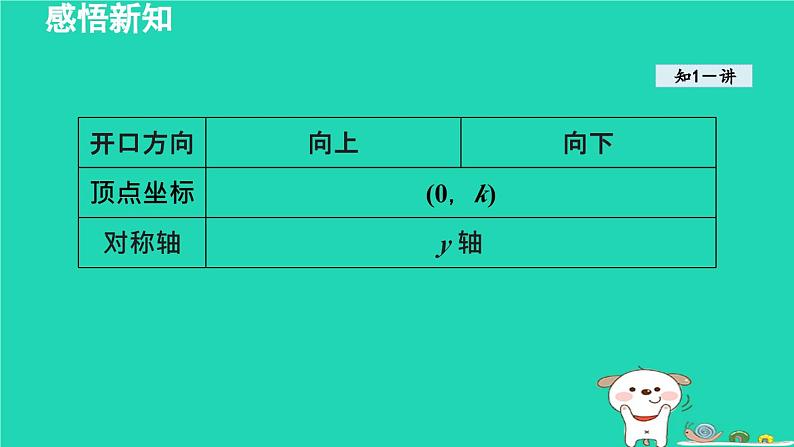
二次函数 y=ax2+k 的图象与二次函数 y=ax2 的图象的关系   它们的形状(开口大小、方向)相同，只是上、下位置不同，二次函数 y=ax2+k 的图象可由二次函数 y=ax2 的图象上下平移 |k|个单位得到 .
要点提醒a 决定抛物线的开口方向和开口大小 .
平移规律口诀“上加下减”表示抛物线的位置上下平移规 律， 即： 抛物线y=ax2+k 是由抛物线y=ax2 上下平移｜k｜个单位长度得到的， “上加”表示当 k 为正数时，向上平移；“下减”表示当k为负数时，向下平移；“纵变横不变”表示坐标的平移规律，即：抛物线上下平移时，其对应点的纵坐标改变，而横坐标不变.
2. 二次函数 y=ax2+k 的图象与性质
3. 二次函数 y=ax2+k 的图象的画法(1)描点法：类比作二次函数 y=ax2 图象的描点法，即按列表→描点→连线的顺序作图 ；(2)平移法：将二次函数 y=ax2 的图象，向上( k>0 )或向下 ( k<0 )平移 |k| 个单位长度，即可得二次函数 y=ax2+k 的图象 .
画出函数 y= － x2 ＋ 1 与 y= － x2 － 1 的图象，并根据图象回答下列问题.
解题秘方：紧扣二次函数图象的平移规律解答 .
方法 1以抛物线 y=－x2 作中介平移：抛物线 y=－x2+1是由抛物线 y=－x2 向上平移 1 个单位得到的， 抛 物 线 y=－x2－1是由抛物线 y=－x2 向下平移 1 个单位得到的 . 因 此 抛 物 线 y=－x2－1 是由抛物线 y=－x2+1 向下平移 2 个单位得到的 .
方法 2以对应点作中介平移：观察图 1.2-6 中的两条抛物线， 抛物线y=－x2 ＋ 1的顶点是( 0，1)， 抛物线 y=－x2－1的顶点是( 0，－1)，因为顶点向下平移了 2个单位，所以将抛物线y=－x2 ＋ 1 向下平移 2 个单位可得到抛物线 y=－x2－1.
(1)抛物线 y＝－x2＋1 经过怎样的平移才能得到抛物线y=－x2－1 ？
解： 列表如下：描点、连线，即得到这两个函数的图象，如图 1.2-6 .
连线时要用光滑的曲线 .
由图象可以看出，抛物线 y=－x2＋1 向下平移2 个单位得到抛物线 y=－x2－1.
(2)对于函数 y＝ －x2＋1， 其图象与 x 轴的公共点的坐标是___________________ ，对称轴是_________ ，顶点坐标是 _________.
(－1，0 ) ，(1，0 )
二次函数 y=a（ x－h） 2 的图象
二次函数 y=a ( x－h ) 2 的图象与二次函数 y=ax2 的图象的关系它们的形状(开口大小、方向)相同，只是左、右位置不同，二次函数 y=a ( x－h ) 2 的图象可由二次函数 y=ax2 的图象左右平移 |h| 个单位得到 .
方法点拨平移规律：左加右减，横变纵不变.1.“左加”表示当h﹤0时，函 数 y=a(x － h)2 的图象可以由函数y=ax2的图象向左平移 |h|个单位得到；2.“右减”表示当h＞0时，函数y=a(x － h)2的图象可以由函数y=ax2 的图象向右平移h个单位得到.3.“横变纵不变”表示坐标的平移规律，即：抛物线左右平移时，对应点的横坐标改变，而纵坐标不变 .
2. 二次函数 y=a ( x－h ) 2的图象
解题秘方：根据函数图象与系数的关系逐一判断即可.
知识储备直线 y=kx+b( k ≠ 0，b ≠ 0) 的位置与 k， b符号的关系：1. k>0 时， 若 b>0，则直线经过第一、二、三象限； 若 b<0，则直线经过第一、三、四象限 .2. k<0 时， 若 b>0，则直线经过第一、二、四象限； 若 b<0，则直线经过第二、三、四象限 .
 二次函数 y=a ( x－h ) 2 +k的图象与二次函数 y=ax2 的图象的关系它们的形状(开口大小、方向)相同，只是位置不同；二次函数y=a ( x－h ) 2 +k的图象可由二次函数 y=ax2 的图象平移得到 ，即先将二次函数 y=ax2 的图
二次函数 y=a（ x－h） 2 +k的图象与性质
象左右平移 |h| 个单位得到二次函数 y=a ( x－h ) 2的图象，再将二次函数 y=a ( x－h ) 2的图象上下平移 |k| 个单位得到二次函数 y=a ( x－h ) 2 +k的图象 .
2. 二次函数 y=a ( x－h ) 2+k的图象与性质
特别解读◆从 y=a ( x－h ) 2+k (a ≠ 0)中可以直接得出抛物线的顶点坐标，所以通常把它称为二次函数的顶点式，顶点坐标是(h， k) .◆对二次项系数相同的二次函数，可以根据两抛物线的顶点位置来判断平移的方式 . 例如：抛物线 y= (x+3) 2+2 的顶点坐标是( － 3，2 ) ，可以看成是由 y=x2的图象先向左平移3个单位，再向上平移2个单位得到的.
[月考·永州冷水滩区李达中学]关于抛物线 y= － 3 ( x+1 ) 2 － 2，下列描述错误的是( )A. 开口向下 B. 对称轴是直线 x= － 1C. 函数最大值是 － 2 D. 当 x> － 1 时， y 随 x 的增大而增大
解题策略解答抛物线 y=a ( x－h ) 2+k的开口方向、对称轴、顶点坐标、最值、增减性等问题，首先必须弄清顶点式 y=a ( x－h ) 2+k中 a， h，k 与开口方向、对称轴、顶点坐标、最值、增减性间的关系，比较题中给出的相关数据与 a，h， k 间的关系， 再结合相关知识按题目要求解答 .
解题秘方：紧扣二次函数 y=a (x － h) 2+k 的图象与性质逐一判断 .
解：∵ a= － 3<0，∴抛物线的开口向下， A 正确；对称轴为直线 x= － 1， B 正确；∵顶点坐标为( － 1， － 2 ) ，抛物线的开口向下，∴函数有最大值，为 － 2， C 正确；当 x> － 1 时， y 随 x 的增大而减小， D 错误 .
二次函数 y=ax2， y=ax2+k， y=a（ x-h） 2， y=a（ x-h） 2+k之间的关系(拓展点)
特别解读1. 抛物线 y=ax2， y=ax2+k， y=a ( x － h ) 2，y=a ( x － h )2+k 中a 值相等，所以这四条抛物线的形状、大小完全一样，故它们之间可通过互相平移得到 .2. 抛物线的平移方法是“左加右减，上加下减”，所不同的是，左右平移时，只针对 h进行变化，而上下平移时，只针对 k 进行变化，可简记为：左加右减自变量，上加下减常数项 .
3. 二次函数 y=a ( x － h )2+k的图象与二次函数y=ax2的图象 的平移关系：既可以先上下平移再左右平移；也可以先左右平移再上下平移 .
3. 抛物线的翻折与旋转规律：(1)将抛物线 y=a(x－h) 2+k 关于 x 轴对称后，得到抛物线 y=－a( x－h) 2－k.(2)将抛物线 y=a( x－h) 2+k 关于 y 轴对称后，得到抛物线 y=a(x+h) 2+k.
(3)将抛物线 y=a(x－h) 2+k 关于原点对称后，得到抛物线 y=－a(x+h) 2－k.(4)将抛物线 y=a( x－h) 2+k 关于顶点( h， k)对称后，得到抛物线 y=－a( x－h) 2+k.(5)将抛物线 y=a( x－h) 2+k 关于点( m， n)对称后，得到抛物线 y=－a(x+h－2m) 2+2n－k.
解题技巧◆“左加右减自变量，上加下减常数项”，抛 物 线 左 右 平 移时，只有 h 发生变化；上下平移时，只有 k 发生变化，反之，根据 h 值的变化可以确定左右平 移 的 方 向 和 距离；根据 k 值的变化可以确定上下平移的方向和距离 .◆画二次函数 y=a ( x － h )2+k ( a ≠ 0 ) 的图象的关键是先确定顶点坐标，再列表取值，也可以不列表，但要将 x，y的对应值在图象中标出来 .
(1)求出 a， h， k 的值 .
(3)观察 y=a ( x－h ) 2+k的图象，当 x____ 时， y随 x 的增大而增大；当 x_________时，函数有最     ______值，最________值是______.(4)观察 y=a ( x－h ) 2+k的图象，你能说出对于一切 x 的值， y 的取值范围吗？
由图象知，对于一切 x 的值，总有 y ≤ 2.