初中数学湘教版（2024）九年级下册1.1 二次函数习题ppt课件

这是一份初中数学湘教版（2024）九年级下册1.1 二次函数习题ppt课件，共32页。PPT课件主要包含了点方法等内容，欢迎下载使用。
(母题：教材P31练习T1) 如图(a)是一座抛物线形拱桥侧面示意图．水面宽AB与桥长CD均为24 m，在距离D点6 m的E处，测得桥面到桥拱的距离EF为1.5 m，以桥拱顶点O为原点，桥面为x轴建立平面直角坐标系.
(1)求桥拱顶部O与水面之间的距离．
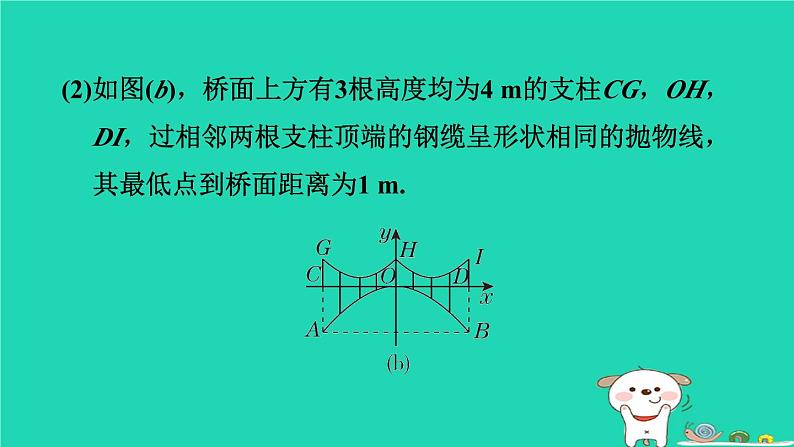
(2)如图(b)，桥面上方有3根高度均为4 m的支柱CG，OH，DI，过相邻两根支柱顶端的钢缆呈形状相同的抛物线，其最低点到桥面距离为1 m.
①求出其中一条钢缆所在抛物线的函数表达式；
②为庆祝节日，在钢缆和桥拱之间竖直装饰若干条彩带，求彩带长度的最小值．
一次足球训练中，小明从球门正前方8 m的A处射门，球射向球门的路线呈抛物线．当球飞行的水平距离为6 m时，球达到最高点，此时球离地面3 m．已知球门高OB为2.44 m，现以O为原点建立如图所示的直角坐标系．
(1)求抛物线的函数表达式，并通过计算判断球能否射进球门(忽略其他因素)．
(2)对本次训练进行分析，若射门路线的形状、最大高度均保持不变，则当时他应该带球向正后方移动多少米射门，才能让足球经过点O正上方2.25 m处？
[2022·无锡]某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙(墙的长度为 10 m)，另外三面用栅栏围成，中间再用栅栏把它分成两个面积比为1∶2的矩形，已知栅栏的总长度为24 m，设较小矩形与墙平行的一边长为x m(如图)．
(1)若矩形养殖场的总面积为36 m2，求此时x的值．
(2)当x为多少时，矩形养殖场的总面积最大？最大值为多少？
求二次函数的最值时，不要盲目地认为顶点的纵坐标就是函数的最值．要结合实际意义确定自变量的取值范围，根据二次函数增减性求出该范围内的最值．
某工厂计划从A，B两种产品中选择一种生产并销售，每日产销x件．已知A产品成本价m元/件(m为常数，且4≤m≤6，售价8元/件，每日最多产销500件，同时每日共支付专利费30元；B产品成本价12元/件，售价20元/件，每日最多产销300件，同时每日支付专利费y元，y(元)与每日产销x(件)满足关系式y＝80＋0.01x2.
(1)若产销A，B两种产品的日利润分别为w1元，w2元，请分别写出w1，w2与x的函数关系式，并写出x的取值范围.
【解】根据题意，得w1＝(8－m)x－30(0≤x≤500)，w2＝(20－12)x－(80＋0.01x2)＝－0.01x2＋8x－80(0≤x≤300)．
(2)分别求出产销A，B两种产品的最大日利润(A产品的最大日利润用含m的代数式表示)．
【解】∵8－m>0，∴w1随x的增大而增大，又0≤x≤500，∴当x＝500时，w1有最大值，即w1最大＝－500m＋3 970(元).∵w2＝－0.01x2＋8x－80＝－0.01(x－400)2＋1 520.又∵－0.01＜0，对称轴为直线x＝400，∴当0≤x≤300时，w2随x的增大而增大，∴当x＝300时，w2最大＝－0.01×(300－400)2＋1 520＝1 420(元)．
(3)为获得最大日利润，该工厂应该选择产销哪种产品？并说明理由．[利润＝(售价－成本)×产销数量－专利费]
【解】①若w1最大＝w2最大，即－500m＋3 970＝1 420，解得m＝5.1；②若w1最大＞w2最大，即－500m＋3 970＞1 420，解得m5.1.又4≤m≤6，综上可得，为获得最大日利润：当m＝5.1时，选择A，B产品产销均可；当4≤m