广东省茂名市电白县2024-2025学年数学九年级第一学期开学统考试题【含答案】

这是一份广东省茂名市电白县2024-2025学年数学九年级第一学期开学统考试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
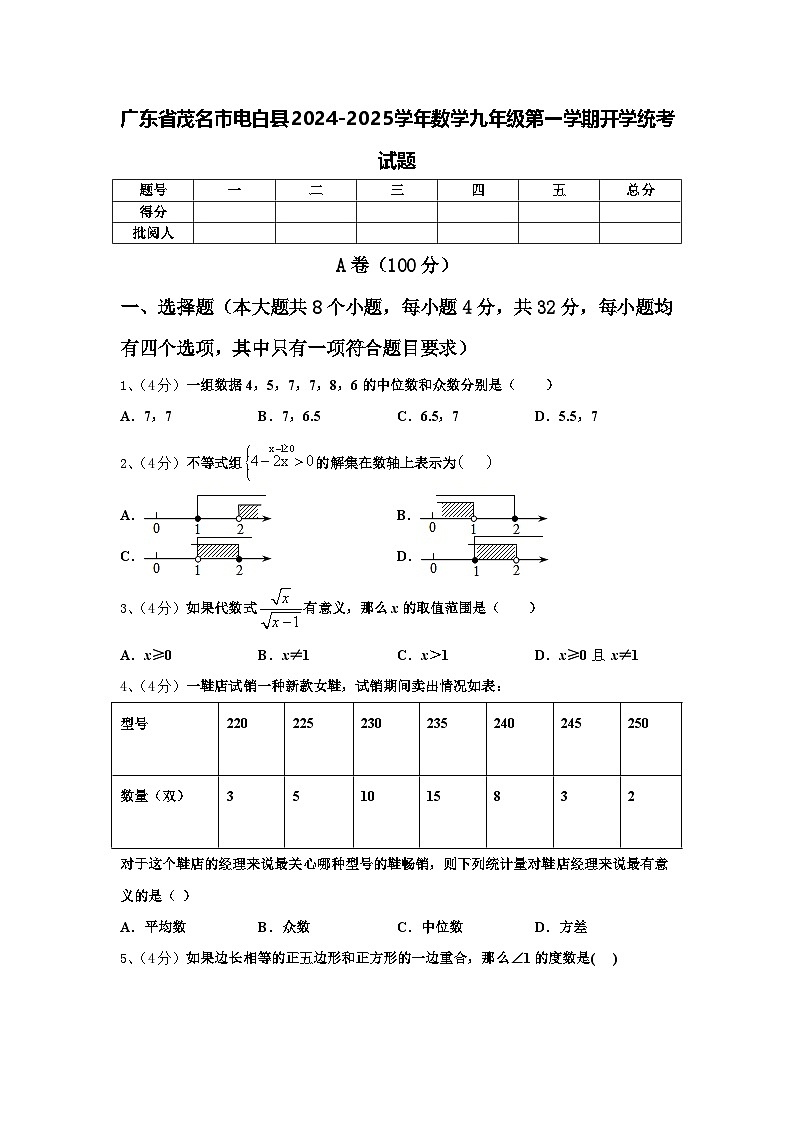
1、（4分）一组数据4，5，7，7，8，6的中位数和众数分别是（ ）
A．7，7B．7，6.5C．6.5，7D．5.5，7
2、（4分）不等式组的解集在数轴上表示为
A．B．
C．D．
3、（4分）如果代数式有意义，那么x的取值范围是（ ）
A．x≥0B．x≠1C．x＞1D．x≥0且 x≠1
4、（4分）一鞋店试销一种新款女鞋，试销期间卖出情况如表：
对于这个鞋店的经理来说最关心哪种型号的鞋畅销，则下列统计量对鞋店经理来说最有意义的是（ ）
A．平均数B．众数C．中位数D．方差
5、（4分）如果边长相等的正五边形和正方形的一边重合，那么∠1的度数是( )
A．30°B．15°C．18°D．20°
6、（4分）下列计算正确的是
A．B．
C．D．
7、（4分）菱形ABCD对角线交于O点，E，F分别是AD、CD的中点，连结EF，若EF=3，OB=4，则菱形面积（ ）
A．24B．20C．12D．6
8、（4分）下列计算正确的是（ ）
A．＝3B．＝﹣3C．＝±3D．（﹣）2＝3
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）直角三角形的一条直角边长是另一条直角边长的2倍,斜边长是10,则较短的直角边的长为___________.
10、（4分）若∠BAC＝30°，AP平分∠BAC，PD∥AC，且PD＝6，PE⊥AC，则PE＝________.
11、（4分）一次函数y＝k(x－1)的图象经过点M(－1，－2)，则其图象与y轴的交点是__________．
12、（4分）如图，设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去.则第2016个正方形的边长为_____
13、（4分）已知一次函数的图象经过两点，，则这个函数的表达式为__________．
三、解答题（本大题共5个小题，共48分）
14、（12分）我们知道平行四边形有很多性质，现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论．
（发现与证明）▱ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连结B′D．
结论1：△AB′C与▱ABCD重叠部分的图形是等腰三角形；
结论2：B′D∥AC
…
（应用与探究）
在▱ABCD中，已知BC=2，∠B=45°，将△ABC沿AC翻折至△AB′C，连结B′D．若以A、C、D、B′为顶点的四边形是正方形，求AC的长．(要求画出图形)
15、（8分）问题情境：在中，，点是的中点，以为角的顶点作．
感知易证：（1）如图1，当射线经过点时，交边于点.将从图1中的位置开始，绕点按逆时针方向旋转，使射线、始终分别交边，于点、，如图2所示，易证，则有．
操作探究：（2）如图2，与是否相似，若相似，请证明；若不相似，请说明理由；
拓展应用：（3）若，直接写出当（2）中的旋转角为多少度时，与相似．
16、（8分）（1）计算：；
（2）已知x＝2−，求(7+4)x2+(2+)x+的值
17、（10分）在矩形ABCD中，对角线AC、BD交于点O，AE平分∠BAD交BC于点E，若∠CAE＝15°．
(1)求证：△AOB是等边三角形；
(2)求∠BOE的度数．
18、（10分）如图，在四边形中，，，，点是的中点．点以每秒1个单位长度的速度从点出发，沿向点运动；同时，点以每秒2个单位长度的速度从点出发，沿向点运动．点停止运动时，点也随之停止运动．求当运动时间为多少秒时，以点，，，为顶点的四边形是平行四边形．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）经过多边形一个顶点共有5条对角线，若这个多边形是正多边形，则它的每一个外角是__度．
20、（4分）如图，在正方形中，点是对角线上一点，连接，将绕点逆时针方向旋转到，连接，交于点，若，，则线段的长为___________．
21、（4分）计算：_____．
22、（4分）关于x的分式方程的解为非正数，则k的取值范围是____．
23、（4分）已知点 A（2，a），B（3，b）在函数 y=1﹣x 的图象上，则 a 与 b 的大小关系是_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）已知一次函数过点（－2，5），和直线，分别在下列条件下求这个一次函数的解析式.
（1）它的图象与直线平行；
（2）它的图象与y轴的交点和直线与y轴的交点关于轴对称.
25、（10分）如图，矩形的长，宽，现将矩形的一角沿折痕翻折，使得点落在边上，求点的位置（即的长）。
26、（12分）列方程（组）及不等式（组）解应用题：
水是生命之源.为了鼓励市民节约用水，江夏区水务部门实行居民用水阶梯式计量水价政策；若居民每户每月用水量不超过10立方米，每立方米按现行居民生活用水水价收费（现行居民生活用水水价=基本水价+污水处理费）；若每户每月用水量超过10立方米，则超过部分每立方米在基本水价基础上加价100%，但每立方米污水处理费不变.
下面表格是某居民小区4月份甲、乙两户居民生活用水量及缴纳生活用水水费的情况统计：
4月份居民用水情况统计表
（注：污水处理的立方数=实际生活用水的立方数）
（1）求每立方米的基本水价和每立方米的污水处理费各是多少？
（2）设这个小区某居民用户5月份用水立方米，需要缴纳的生活用水水费为元.若他5月份生活用水水费计划不超过64元，该用户5月份最多可用水多少立方米？
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据中位数与众数的概念和求解方法进行求解即可.
【详解】
将数据从小到大排列：4、5、6、7、7、8，
所以中位数为=6.5，众数是7，
故选C.
本题考查了中位数和众数，熟练掌握相关定义以及求解方法是解题的关键.①给定n个数据，按从小到大排序，如果n为奇数，位于中间的那个数就是中位数；如果n为偶数，位于中间两个数的平均数就是中位数．任何一组数据，都一定存在中位数的，但中位数不一定是这组数据里的数．②给定一组数据，出现次数最多的那个数，称为这组数据的众数．
2、D
【解析】
分别求出不等式组中每一个不等式的解集，再求出其公共解集，并在数轴上表示出来即可．
【详解】
：，
由得，，
由得，，
故此不等式组的解集为：，
在数轴上表示为：
故选D．
本题考查了解一元一次不等式组以及在数轴上表示不等式组的解集，熟练掌握不等式组解集的确定方法“同大取大，同小取小，大小小大中间找，大大小小无解了”是解题的关键.在数轴上表示时要注意实心圆点与空心圆点的区别．
3、C
【解析】
根据二次根式中被开方数是非负数，分式分母不为零列出不等式即可求出答案.
【详解】
根据题意可知，解得x>1，
故答案选C.
本题考查的是二次根式和分式存在有意义的条件，熟知该知识点是解题的关键.
4、B
【解析】
众数是一组数据中出现次数最多的数，可能不止一个，对这个鞋店的经理来说，他最关注的是数据的众数．
【详解】
解：对这个鞋店的经理来说，他最关注的是哪一型号的卖得最多，即是这组数据的众数．
故选B．
5、C
【解析】
∠1的度数是正五边形的内角与正方形的内角的度数的差，根据多边形的内角和定理求得角的度数，进而求解．
【详解】
∵正五边形的内角的度数是×（5-2）×180°=108°，正方形的内角是90°，
∴∠1=108°-90°=18°．故选C
本题考查了多边形的内角和定理、正五边形和正方形的性质，求得正五边形的内角的度数是关键．
6、D
【解析】
根据二次根式的运算法则逐项计算即可判断.
【详解】
解：A、和不是同类二次根式，不能合并，故错误；
B、=2，故错误；
C、=，故错误；
D、==2，故正确.
故选D.
本题考查了二次根式的四则运算.
7、A
【解析】
根据菱形的对角线互相垂直且平分，所以可得菱形的面积等于倍的对角线的乘积.
【详解】
解：根据E，F分别是AD、CD的中点，EF=3
可得AC=6,
OB=4可得BD=8
所以菱形ABCD的面积为：
故选A.
本题主要考查菱形对角线的性质，关键在于菱形的对角线平分且垂直.
8、D
【解析】
根据二次根式的运算法则和性质逐个进行化简分析.
【详解】
A. , 本选项错误；
B. , 本选项错误；
C. , 本选项错误；
D. ，本选项正确.
故选D
本题考核知识点：二次根式的化简. 解题关键点：熟记二次根式的性质.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1
【解析】
根据边之间的关系，运用勾股定理，列方程解答即可．
【详解】
由题意可设两条直角边长分别为x，2x，
由勾股定理得x2+(2x)2=(1)2，
解得x1=1，x2=-1舍去），
所以较短的直角边长为1．
故答案为：1
本题考查了一元二次方程和勾股定理的应用，解题的关键是根据勾股定理得到方程，转化为方程问题．
10、1
【解析】
分析：过P作PF⊥AB于F，根据平行线的性质可得∠FDP=∠BAC=10°，再根据10度所对的边是斜边的一半可求得PF的长，最后根据角平分线的性质即可求得PE的长．
详解：过P作PF⊥AB于F．∵PD∥AC，∴∠FDP=∠BAC=10°，∴在Rt△PDF中，PF=PD=1．
∵AP平分∠BAC，PE⊥AC于E，PF⊥AB于F，∴PE=PF=1．
故答案为1．

点睛：本题考查了角平分线的性质，直角三角形10°角所对的直角边等于斜边的一半的性质，平行线的性质，熟记性质是解题的关键．
11、 (0，-1)
【解析】
由图象经过点M，故将M(-1，-2)代入即可得出k的值．
【详解】
解：∵一次函数y=k(x-1)的图象经过点M(-1，-2)，
则有k(-1-1)=-2，解得k=1，
所以函数解析式为y=x-1，
令x=0代入得y=-1，
故其图象与y轴的交点是(0，-1)．
故答案为(0，-1)．
本题考查待定系数法求函数解析式，难度不大，直接代入即可．
12、（）1．
【解析】
首先求出AC、AE、HE的长度，然后猜测命题中隐含的数学规律，即可解决问题．
【详解】
∵四边形ABCD为正方形，
∴AB=BC=1，∠B=90°，
∴AC2=12+12，AC=；
同理可求：AE=（）2，HE=（）3…，
∴第n个正方形的边长an=（）n-1，
∴第2016个正方形的边长为（）1，
故答案为（）1．
本题考查了勾股定理在直角三角形中的运用，考查了学生找规律的能力，本题中找到an的规律是解题的关键．
13、
【解析】
设一次函数的解析式是：y=kx+b，然后把点，代入得到一个关于k和b的方程组，从而求得k、b的值，进而求得函数解析式．
【详解】
解：设一次函数的解析式是：y=kx+b，
根据题意得：，
解得：，
则一次函数的解析式是：．
故答案是：．
本题考查了待定系数法求函数的解析式，先根据条件列出关于字母系数的方程，解方程求解即可得到函数解析式．当已知函数解析式时，求函数中字母的值就是求关于字母系数的方程的解．
三、解答题（本大题共5个小题，共48分）
14、 [发现与证明]：证明见解析；[应用与探究]：AC的长为或1．
【解析】
[发现与证明]由平行四边形的性质得出∠EAC=∠ACB，由翻折的性质得出∠ACB=∠ACB′，证出∠EAC=∠ACB′，得出AE=CE；得出DE=B′E，证出∠CB′D=∠B′DA= (180°-∠B′ED)，由∠AEC=∠B′ED，得出∠ACB′=∠CB′D，即可得出B′D∥AC；
[应用与探究]：分两种情况：①由正方形的性质得出∠CAB′=90°，得出∠BAC=90°，再由三角函数即可求出AC；
②由正方形的性质和已知条件得出AC=BC=1．
【详解】
解：[发现与证明]：∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∴∠EAC=∠ACB，
∵△ABC≌△AB′C，
∴∠ACB=∠ACB′，BC=B′C，
∴∠EAC=∠ACB′，
∴AE=CE，
即△ACE是等腰三角形；
∴DE=B′E，
∴∠CB′D=∠B′DA=(180°-∠B′ED)，
∵∠AEC=∠B′ED，
∴∠ACB′=∠CB′D，
∴B′D∥AC；
[应用与探究]：分两种情况：①如图1所示：
∵四边形ACDB′是正方形，
∴∠CAB′=90°，
∴∠BAC=90°，
∵∠B=45°，
∴AC=BC=；
②如图1所示：AC=BC=1；
综上所述：AC的长为或1．
本题考查了平行四边形的性质、正方形的性质、翻折变换、等腰三角形的判定以及平行线的判定；熟练掌握平行四边形的性质、翻折变换的性质，并能进行推理计算是解决问题的关键．
15、（1）CD；（2）△BDF∽△DEF，理由见详解；（3）10°或40°．
【解析】
（1）如图2，根据∠EDF＝∠B及三角形外角性质可得∠BFD＝∠CDE，再根据∠B＝∠C即可得到△BFD∽△CDE解决问题．
（2）如图2，由（2）得△BFD∽△CDE，则有，由D是BC的中点可得．再根据∠B＝∠EDF即可得到△BDF∽△DEF．
（3）由∠B＝∠C＝50°可得∠BAC＝80°，AB＝AC，再由BD＝CD可得AD⊥BC．若△DEF与△ABC相似，由△BDF∽△DEF可得△BDF与△ABC相似，从而得到∠BDF＝∠BAC＝80°，或∠BDF＝∠C＝50°，即可解决问题．
【详解】
解：（1）如图2，

∵AB＝AC
∴∠B＝∠C，
∵∠FDC是△BFD的一个外角，
∴∠FDC＝∠B+∠BFD．
∵∠FDC＝∠FDE+∠EDC，∠EDF＝∠B，
∴∠BFD＝∠CDE．
∵∠B＝∠C，
∴△BFD∽△CDE；
∴．
（2）如图2，结论：△BDF∽△DEF．

理由：由（1）得．
∵D是BC的中点，
∴BD＝CD，
∴，
又∵∠B＝∠EDF，
∴△BDF∽△DEF．
（3）连接AD，如图3，

∵∠B＝∠C＝50°，
∴∠BAC＝80°，AB＝AC．
∵BD＝CD，
∴AD⊥BC．
若△DEF与△ABC相似，
∵△BDF∽△DEF，
∴△BDF与△ABC相似，
∴∠BDF＝∠BAC＝80°，或∠BDF＝∠C＝50°，
∴∠ADF＝90°﹣80°＝10°，或∠ADF＝90°﹣50°＝40°，
∴当（2）中的旋转角为10°或40°时，△DEF与△ABC相似．
本题属于相似形综合题，主要考查了相似三角形的判定与性质、等腰三角形的判定与性质、三角形的外角性质、三角形内角和定理等知识，解题的关键是正确寻找相似三角形的判定条件，属于中考常考题型．
16、（1）9-2；（2）2+
【解析】
（1）根据二次根式的运算法则即可求出答案．
（2）根据完全平方公式进行化简，然后将x的值代入即可求出答案．
【详解】
（1）原式=6+3−2+1−1
=9-2
（2）原式=（+2）2x2+（2+）x+
=（+2）2（2-）2+（2+）（2-）+
=（4-3）2+4-3+
=1+1+
=2+
本题考查学生的运算能力，解题的关键是熟练运用二次根式的运算法则，本题属于基础题型．
17、 (1)证明见解析；(2)∠BOE＝75°.
【解析】
(1)由矩形ABCD，得到OA＝OB，根据AE平分∠BAD，∠CAE＝15°，即可证明△AOB是等边三角形;
(2)由等边三角形的性质，推出AB＝OB，求出∠OBC的度数，根据等边三角形和等腰直角三角形的性质得到OB＝BE，然后可求出∠BOE．
【详解】
(1)证明：∵四边形ABCD是矩形，
∴OA＝OB，
∵AE平分∠BAD，
∴∠BAE＝∠DAE＝45°，
∵∠CAE＝15°，
∴∠BAC＝60°，
∴△AOB是等边三角形．
(2)∵△AOB是等边三角形，
∴AB＝OB，∠ABO＝60°，
∴∠OBC＝90°﹣60°＝30°，
∵∠BAE＝∠BEA＝45°
∵AB＝OB＝BE，
∴∠BOE＝∠BEO＝(180°﹣30°)＝75°．
本题主要考查了三角形的内角和定理，矩形的性质，等边三角形的性质和判定，角平分线的性质，等腰三角形的判定等知识点．
18、t为2或秒
【解析】
由已知以点P，Q，E，D为顶点的四边形是平行四边形有两种情况，（1）当Q运动到E和C之间，（2）当Q运动到E和B之间，根据平行四边形的判定，由AD∥BC，所以当PD=QE时为平行四边形．根据此设运动时间为t，列出关于t的方程求解．
【详解】
解：由题意可知，AP=t，CQ=2t，CE=BC=8
∵AD∥BC，
∴当PD=EQ时，以点P，Q，E，D为顶点的四边形是平行四边形．
①当2t＜8，即t＜4时，点Q在C，E之间，如图甲．
此时，PD=AD-AP=6-t，EQ=CE-CQ=8-2t，
由6-t=8-2t，得t=2；
②当8