新高考数学专题复习专题01函数图像的识别与辨析专题练习(学生版+解析)

这是一份新高考数学专题复习专题01函数图像的识别与辨析专题练习(学生版+解析)，共25页。试卷主要包含了、由函数的解析式识别图像等内容，欢迎下载使用。

题型一 、由函数的解析式识别图像
函数图象的识辨可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、筛选选项
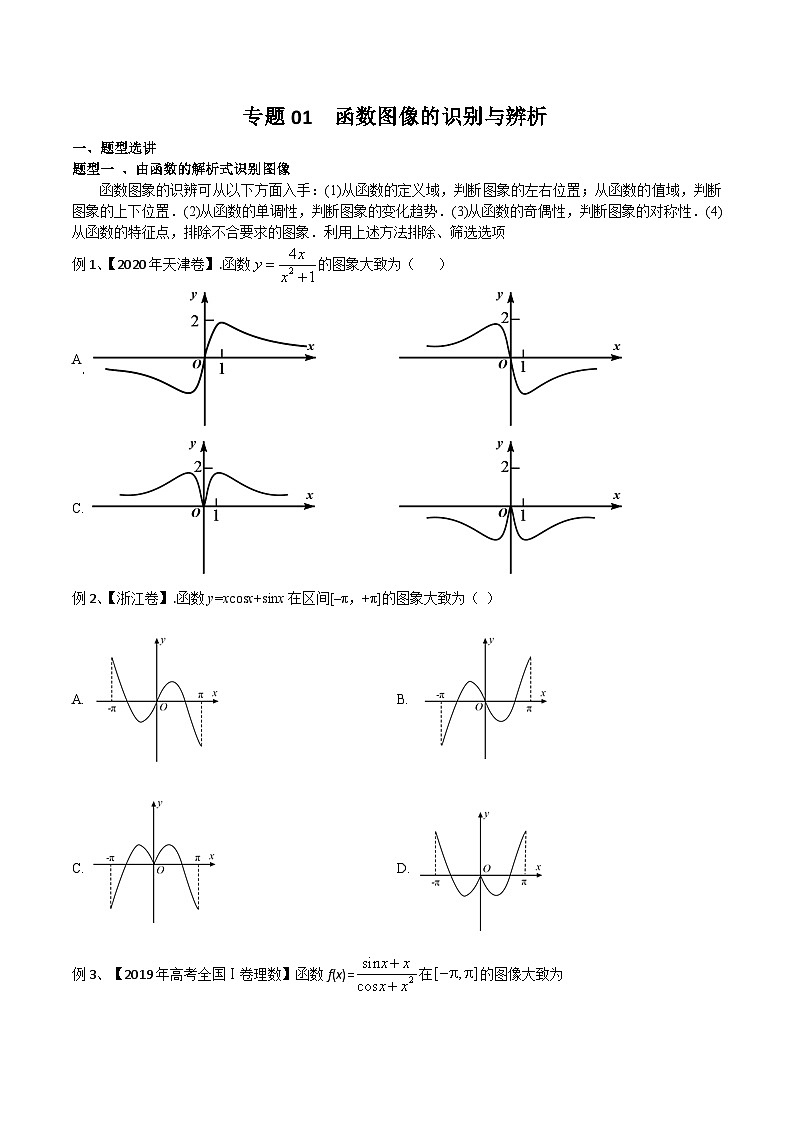
例1、【2020年天津卷】.函数的图象大致为（ ）
A
C.
例2、【浙江卷】.函数y=xcsx+sinx在区间[–π，+π]的图象大致为（ ）
A. B.
C. D.
例3、【2019年高考全国Ⅰ卷理数】函数f(x)=在的图像大致为
A．B．
C．D．
题型二、由函数的图像辨析函数的解析式
由函数的图像确定解析式，首先要观察函数的图像，可以从以下几个方面入手：（1）观察函数的对称性，判断函数的奇偶性；（2）观察图像所在象限，判断函数的定义域和值域；（3）从图像中观察一些特殊位置以及图像的发展趋势；结合上面的信息进行对函数解析式的排除。
(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、筛选选项
例4、（2020届山东省九校高三上学期联考）若函数的大致图像如图所示，则的解析式可以为（ ）
A．B．
C．D．
例5、（2020届浙江省嘉兴市3月模拟）已知函数的图象如图所示，则的解析式最有可能是（ ）
A．B．C．D．
题型三、图像识别与辨析的综合
解决此类问题，要对选项进行逐一进行排除，由此题目要对参数进行讨论，涉及的知识点往往与对数函数和指数函数有关，因此，要掌握指对数函数的图像和性质。
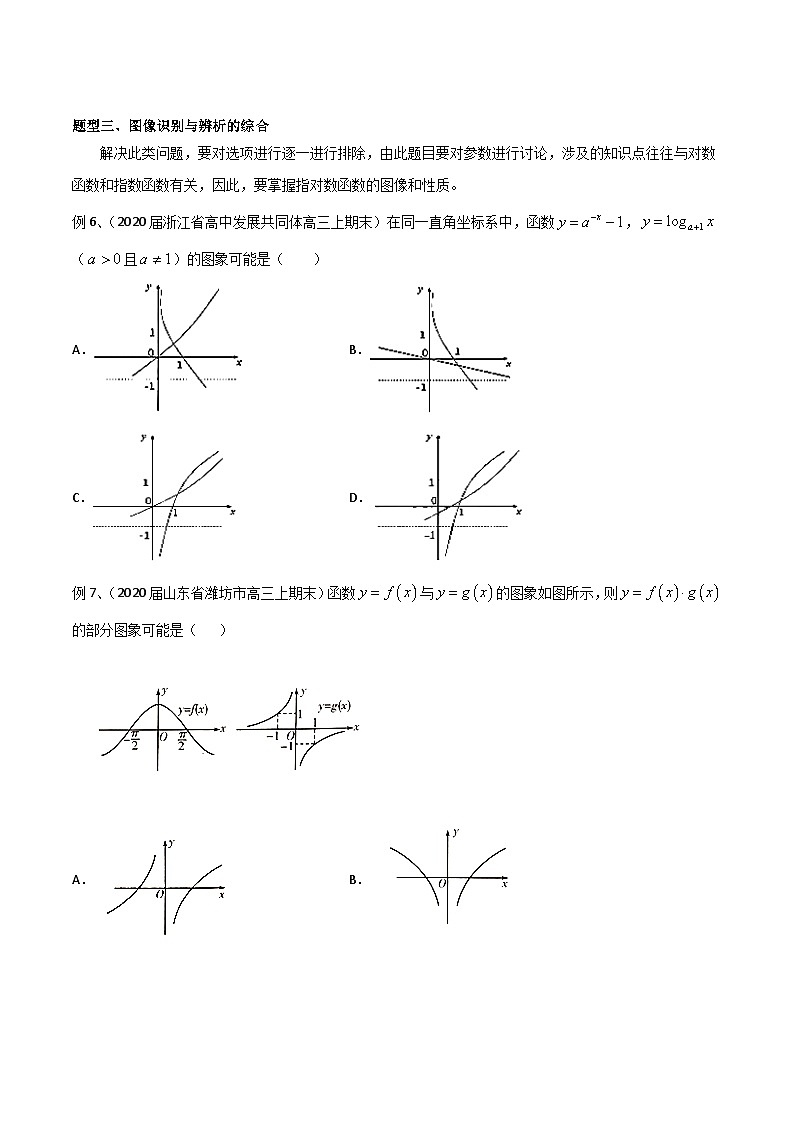
例6、（2020届浙江省高中发展共同体高三上期末）在同一直角坐标系中，函数，（且）的图象可能是（ ）
A．B．
C．D．
例7、（2020届山东省潍坊市高三上期末）函数与的图象如图所示，则的部分图象可能是（ ）
A．B．
C．D．
例8、(2015安徽)函数的图象如图所示，则下列结论成立的是
A．，， B．，，
C．，， D．，，
二、达标训练
1、【2019年高考全国Ⅲ卷理数】函数在的图像大致为
A．B．
C．D．
2、【2019年高考浙江】在同一直角坐标系中，函数，(a>0，且a≠1)的图象可能是
3、【2018年高考全国Ⅱ卷理数】函数的图像大致为
4、【2018年高考全国Ⅲ卷理数】函数的图像大致为
5、【2018年高考浙江】函数y=sin2x的图象可能是
A． B．
C． D．
6、（2020届山东省泰安市高三上期末）函数的部分图象是（ ）
A．B．
C．D．
7、（2020届山东省潍坊市高三上期中）函数的大致图象为（ ）
A．B．
C．D．
8、（2020届山东省滨州市三校高三上学期联考）函数的图象大致为（ ）
A．B．
C．D．
9、（2020届山东省济宁市高三上期末）函数，的图象大致为( )
A．B．
C．D．
10、（2020届浙江省之江教育评价联盟高三第二次联考）函数的部分图象大致为（ ）
A．B．
C．D．
11、（2020届浙江省绍兴市高三4月一模）已知，且，若，则的图象可能是( )
A．B．
C．D．
12、（2020届浙江省温州市高三4月二模）定义在上的函数满足，且为奇函数，则的图象可能是（ ）
A．B．C．D．
13、（2020届浙江省杭州市第二中学高三3月月考）函数的部分图象可能是（ ）
A． B．
C． D．
14、（2020届浙江省十校联盟高三下学期开学）已知函数，则的图像大致是（ ）
A．B．
C．D．
15、（2020届浙江省温丽联盟高三第一次联考）如图，对应此函数图象的函数可能是( )
A．B．
C．D．
专题01 函数图像的识别与辨析
题型选讲
题型一 、由函数的解析式识别图像
函数图象的识辨可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、筛选选项
例1、【2020年天津卷】.函数的图象大致为（ ）
A
C.
【答案】A
【解析】由函数的解析式可得：，则函数为奇函数，其图象关于坐标原点对称，选项CD错误；
当时，，选项B错误.
故选：A.
例2、【浙江卷】.函数y=xcsx+sinx在区间[–π，+π]的图象大致为（ ）
A. B.
C. D.
【答案】A
【解析】因为，则，
即题中所给的函数为奇函数，函数图象关于坐标原点对称，
据此可知选项CD错误；
且时，，据此可知选项B错误.
故选：A.
例3、【2019年高考全国Ⅰ卷理数】函数f(x)=在的图像大致为
A．B．
C．D．
【答案】D
【解析】由，得是奇函数，其图象关于原点对称．
又，可知应为D选项中的图象．
故选D．
题型二、由函数的图像辨析函数的解析式
由函数的图像确定解析式，首先要观察函数的图像，可以从以下几个方面入手：（1）观察函数的对称性，判断函数的奇偶性；（2）观察图像所在象限，判断函数的定义域和值域；（3）从图像中观察一些特殊位置以及图像的发展趋势；结合上面的信息进行对函数解析式的排除。
(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、筛选选项
例4、（2020届山东省九校高三上学期联考）若函数的大致图像如图所示，则的解析式可以为（ ）
A．B．
C．D．
【答案】C
【解析】
对四个选项解析式分析发现B，D两个均为偶函数，图象关于y轴对称，与题不符，故排除；
极限思想分析，，A错误；
，C符合题意.
故选：C
例5、（2020届浙江省嘉兴市3月模拟）已知函数的图象如图所示，则的解析式最有可能是（ ）
A．B．C．D．
【答案】A
【解析】
选项B、D的函数定义域为，和图象不匹配，错误；
选项C函数为减函数，和图象不匹配，错误；
选项A函数的定义域为R，且为增函数，正确.
故选：A
题型三、图像识别与辨析的综合
解决此类问题，要对选项进行逐一进行排除，由此题目要对参数进行讨论，涉及的知识点往往与对数函数和指数函数有关，因此，要掌握指对数函数的图像和性质。
例6、（2020届浙江省高中发展共同体高三上期末）在同一直角坐标系中，函数，（且）的图象可能是（ ）
A．B．
C．D．
【答案】C
【解析】当时，函数在上单调递减且是曲线，向下平移一个单位长度得，排除A，B，C，D，没有符合题意的;
当时，函数在上单调递增且是曲线，向下平移一个单位长度得，排除B，当时，，排除D.
此时，函数（且）在上单调递增，排除A.
故选：C.
例7、（2020届山东省潍坊市高三上期末）函数与的图象如图所示，则的部分图象可能是（ ）
A．B．
C．D．
【答案】A
【解析】
由图象可知的图象关于轴对称，是偶函数，的图象关于原点对称，是奇函数，并且定义域，
的定义域是，并且是奇函数，排除B，
又时，，，，排除C,D.
满足条件的只有A.
故选：A
例8、(2015安徽)函数的图象如图所示，则下列结论成立的是
A．，， B．，，
C．，， D．，，
【答案】．C
【解析】∵的图象与轴分别交于，且点的纵坐标与点的横坐标均为正，∴，，故，又函数图象间断的横坐标为正，∴，故．
二、达标训练
1、【2019年高考全国Ⅲ卷理数】函数在的图像大致为
A．B．
C．D．
【答案】B
【解析】设，则，所以是奇函数，图象关于原点成中心对称，排除选项C．
又排除选项D；
，排除选项A，
故选B．
【名师点睛】本题通过判断函数的奇偶性，排除错误选项，通过计算特殊函数值，作出选择．本题注重基础知识、基本计算能力的考查．
2、【2019年高考浙江】在同一直角坐标系中，函数，(a>0，且a≠1)的图象可能是
【答案】D
【解析】当时，函数的图象过定点且单调递减，则函数的图象过定点且单调递增，函数的图象过定点且单调递减，D选项符合；
当时，函数的图象过定点且单调递增，则函数的图象过定点且单调递减，函数的图象过定点且单调递增，各选项均不符合.
综上，选D.
【名师点睛】易出现的错误：一是指数函数、对数函数的图象和性质掌握不熟练，导致判断失误；二是不能通过讨论的不同取值范围，认识函数的单调性.
3、【2018年高考全国Ⅱ卷理数】函数的图像大致为
【答案】B
【解析】为奇函数，舍去A；
，∴舍去D；
时，，单调递增，舍去C.
因此选B.
4、【2018年高考全国Ⅲ卷理数】函数的图像大致为
【答案】D
【解析】函数图象过定点，排除A，B；
令，则，
由得，得或，此时函数单调递增，
由得，得或，此时函数单调递减，排除C.
故选D.
5、【2018年高考浙江】函数y=sin2x的图象可能是
A． B．
C． D．
【答案】D
【解析】令，因为，所以为奇函数，排除选项A,B;
因为时，，所以排除选项C，
故选D．
6、（2020届山东省泰安市高三上期末）函数的部分图象是（ ）
A．B．
C．D．
【答案】A
【解析】， 为奇函数，排除B
当时，恒成立，排除CD
故答案选A
7、（2020届山东省潍坊市高三上期中）函数的大致图象为（ ）
A．B．
C．D．
【答案】A
【解析】函数的定义域为，
，则函数是奇函数，图象关于原点对称，排除，，
当且，，排除.
故选：A.
8、（2020届山东省滨州市三校高三上学期联考）函数的图象大致为（ ）
A．B．
C．D．
【答案】B
【解析】因为，所以，
得，所以为奇函数，排除C；
设，恒成立，所以在，单调递增，所以，
故在上恒成立，排除AD，
故选：B.
9、（2020届山东省济宁市高三上期末）函数，的图象大致为( )
A．B．
C．D．
【答案】B
【解析】
∵，
∴函数为偶函数.故排除选项A，D.
，
∵，
∴当时，取得最大值；当时，取得最小值0.故排除C.
故选：B.
10、（2020届浙江省之江教育评价联盟高三第二次联考）函数的部分图象大致为（ ）
A．B．
C．D．
【答案】D
【解析】
当时，函数值，符合要求的只有选项D.
故选：D.
11、（2020届浙江省绍兴市高三4月一模）已知，且，若，则的图象可能是( )
A．B．
C．D．
【答案】D
【解析】
，
.
结合图象，故排除B，C.
又，故排除A.
D选项满足.
故选：D.
12、（2020届浙江省温州市高三4月二模）定义在上的函数满足，且为奇函数，则的图象可能是（ ）
A．B．C．D．
【答案】D
【解析】
为奇函数，即，函数关于中心对称，排除.
，排除.
故选：.
13、（2020届浙江省杭州市第二中学高三3月月考）函数的部分图象可能是（ ）
A． B．
C． D．
【答案】A
【解析】
因为,所以舍去B，因为，所以舍去D，
因为时，，
因此选A.
14、（2020届浙江省十校联盟高三下学期开学）已知函数，则的图像大致是（ ）
A．B．
C．D．
【答案】C
【解析】
函数，
，
为奇函数，故图象关于原点对称，故排除和，
，
可知当，即时，
当时，时，，从左到右第一个零点为，
因为，取，得，则选项正确.
故选：C.
15、（2020届浙江省温丽联盟高三第一次联考）如图，对应此函数图象的函数可能是( )
A．B．
C．D．
【答案】B
【解析】
由图可知，函数的定义域为，故C错；
函数的图象过点，若，则当时，，故A错；
又函数的图象过点，若，则当时，，故D错；
故选：B．