新高考数学专题复习专题21运用空间向量解决空间角专题练习(学生版+解析)
展开题型一 、异面直线所成的角以及
研究异面直线所成的角首先要注意交的范围,然后转化为有直线的方向向量的夹角。
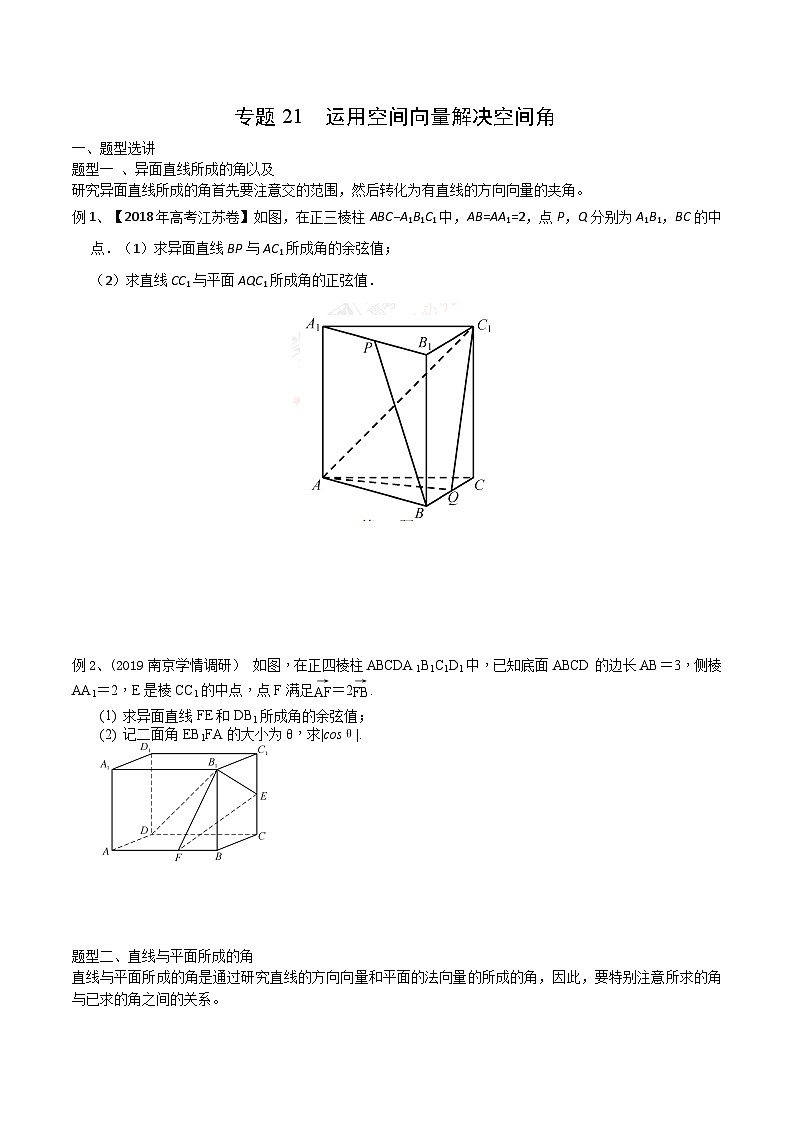
例1、【2018年高考江苏卷】如图,在正三棱柱ABC−A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
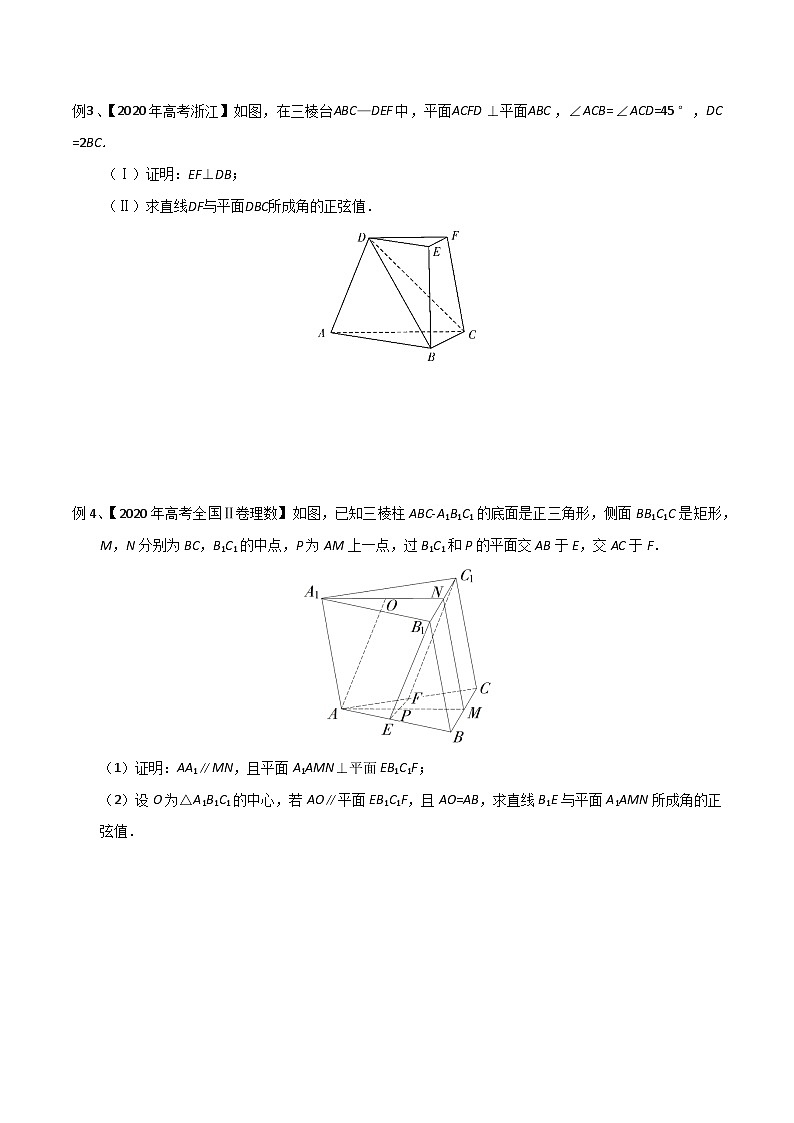
例2、(2019南京学情调研) 如图,在正四棱柱ABCDA1B1C1D1中,已知底面ABCD的边长AB=3,侧棱AA1=2,E是棱CC1的中点,点F满足eq \(AF,\s\up6(→))=2eq \(FB,\s\up6(→)).
(1) 求异面直线FE和DB1所成角的余弦值;
(2) 记二面角EB1FA的大小为θ,求|csθ|.
题型二、直线与平面所成的角
直线与平面所成的角是通过研究直线的方向向量和平面的法向量的所成的角,因此,要特别注意所求的角与已求的角之间的关系。
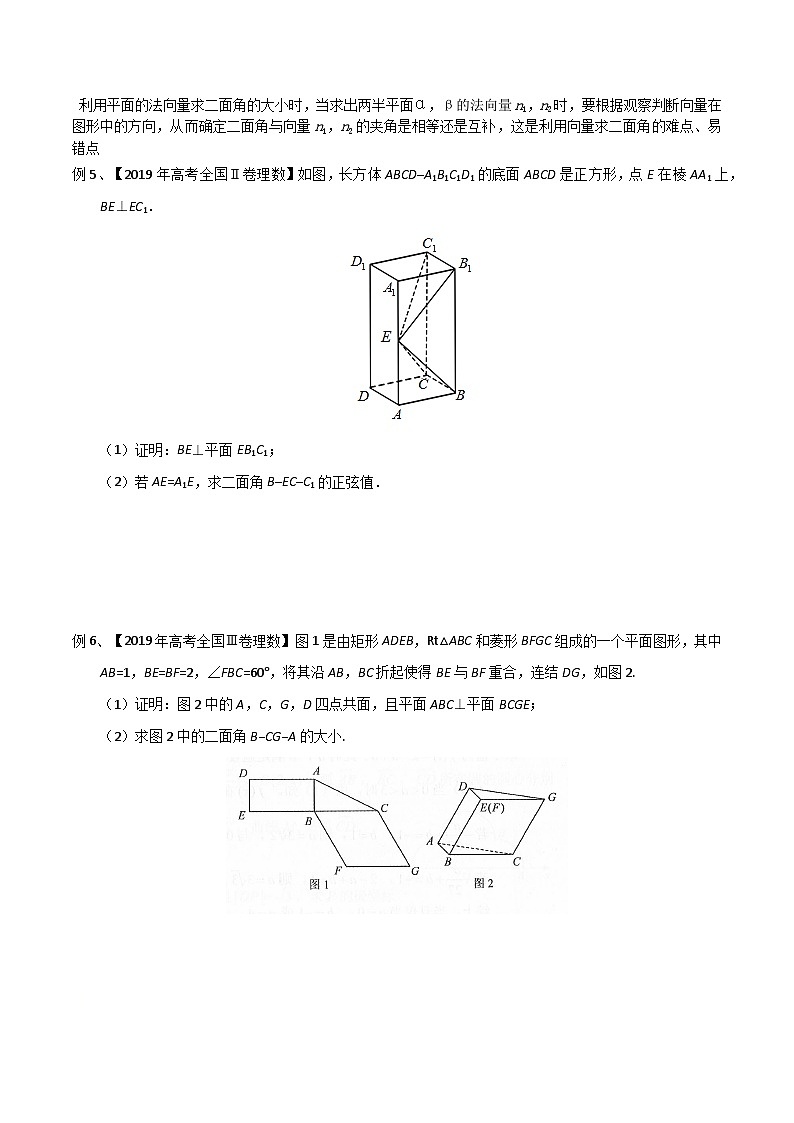
例3、【2020年高考浙江】如图,在三棱台ABC—DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC =2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求直线DF与平面DBC所成角的正弦值.
例4、【2020年高考全国Ⅱ卷理数】如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.
(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F;
(2)设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.
题型三、平面与平面所成的角
利用平面的法向量求二面角的大小时,当求出两半平面α,β的法向量n1,n2时,要根据观察判断向量在图形中的方向,从而确定二面角与向量n1,n2的夹角是相等还是互补,这是利用向量求二面角的难点、易错点
例5、【2019年高考全国Ⅱ卷理数】如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
例6、【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B−CG−A的大小.
例7、(2020届山东省潍坊市高三上期中)如图,在棱长均为的三棱柱中,平面平面,,为与的交点.
(1)求证:;
(2)求平面与平面所成锐二面角的余弦值.
二、达标训练
1、【2019年高考天津卷理数】如图,平面,,.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)若二面角的余弦值为,求线段的长.
2、【2019年高考浙江卷】如图,已知三棱柱,平面平面,,分别是AC,A1B1的中点.
(1)证明:;
(2)求直线EF与平面A1BC所成角的余弦值.
3、【2018年高考全国Ⅰ卷理数】如图,四边形为正方形,分别为的中点,以为折痕把折起,使点到达点的位置,且.
(1)证明:平面平面;
(2)求与平面所成角的正弦值.
4、(2020届山东省九校高三上学期联考)已知四棱柱的底面为菱形,,,,平面,.
(1)证明:平面;
(2)求钝二面角的余弦值.
5、(2020届山东省潍坊市高三上期末)在底面为正方形的四棱锥中,平面平面分别为棱和的中点.
(1)求证:平面;
(2)若直线与所成角的正切值为,求平面与平面所成锐二面角的大小.
6、(2019南京、盐城一模)如图,四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=1,PA=AB=eq \r(2),点E是棱PB的中点.
(1) 求异面直线EC与PD所成角的余弦值;
(2) 求二面角BECD的余弦值.
专题21 运用空间向量解决空间角
一、题型选讲
题型一 、异面直线所成的角以及
研究异面直线所成的角首先要注意交的范围,然后转化为有直线的方向向量的夹角。
例1、【2018年高考江苏卷】如图,在正三棱柱ABC−A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
【答案】(1);(2).
【解析】如图,在正三棱柱ABC−A1B1C1中,设AC,A1C1的中点分别为O,O1,则OB⊥OC,OO1⊥OC,OO1⊥OB,以为基底,建立空间直角坐标系O−xyz.
因为AB=AA1=2,
所以.
(1)因为P为A1B1的中点,所以,
从而,
故.
因此,异面直线BP与AC1所成角的余弦值为.
(2)因为Q为BC的中点,所以,
因此,.
设n=(x,y,z)为平面AQC1的一个法向量,
则即
不妨取,
设直线CC1与平面AQC1所成角为,
则,
所以直线CC1与平面AQC1所成角的正弦值为.
例2、(2019南京学情调研) 如图,在正四棱柱ABCDA1B1C1D1中,已知底面ABCD的边长AB=3,侧棱AA1=2,E是棱CC1的中点,点F满足eq \(AF,\s\up6(→))=2eq \(FB,\s\up6(→)).
(1) 求异面直线FE和DB1所成角的余弦值;
(2) 记二面角EB1FA的大小为θ,求|csθ|.
规范解答 在正四棱柱ABCDA1B1C1D1中,
以{eq \(DA,\s\up6(→)),eq \(DC,\s\up6(→)),eq \(DD1,\s\up6(→))}为正交基底,建立如图所示的空间直角坐标系Dxyz.
因为AB=3,AA1=2,
E是CC1的中点,eq \(AF,\s\up6(→))=2eq \(FB,\s\up6(→)),
所以E(0,3,1),F(3,2,0),B1(3,3,2). (2分)
(1)从而eq \(FE,\s\up6(→))=(-3,1,1),eq \(DB1,\s\up6(→))=(3,3,2).
设异面直线FE和DB1所成的角为α,
则csα=|cs〈eq \(FE,\s\up6(→)),eq \(DB1,\s\up6(→))〉|=eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(-3×3+1×3+1×2,\r(11)×\r(22))))=eq \f(4,\r(11)×\r(22))=eq \f(2\r(2),11).
因此,异面直线FE和DB1所成角的余弦值为eq \f(2\r(2),11). (5分)
(2)设平面B1FE的法向量为n1=(x,y,z).
因为eq \(FE,\s\up6(→))=(-3,1,1),eq \(FB1,\s\up6(→))=(0,1,2),
由eq \b\lc\{(\a\vs4\al\c1(n1·\(FE,\s\up6(→))=0,,n1 ·\(FB1,\s\up6(→))=0,))得eq \b\lc\{(\a\vs4\al\c1(-3x+y+z=0,,y+2z=0,)) 所以eq \b\lc\{(\a\vs4\al\c1(x=-\f(1,3)z,,y=-2z.))
取z=-3,则平面B1FE的一个法向量为n1=(1,6,-3).(8分)
又因为平面AB1F的一个法向量为n2=(1,0,0),
所以cs〈n1,n2〉=eq \f(1,\r(46)×1)=eq \f(\r(46),46).
因此|csθ|=| cs〈n1,n2〉|=eq \f(\r(46),46). (10分)
题型二、直线与平面所成的角
直线与平面所成的角是通过研究直线的方向向量和平面的法向量的所成的角,因此,要特别注意所求的角与已求的角之间的关系。
例3、【2020年高考浙江】如图,在三棱台ABC—DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC =2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求直线DF与平面DBC所成角的正弦值.
【解析】(Ⅰ)如图,过点D作,交直线AC于点,连结OB.
由,得,
由平面ACFD⊥平面ABC得DO⊥平面ABC,所以.
由,得.
所以BC⊥平面BDO,故BC⊥DB.
由三棱台得,所以.
(Ⅱ)方法一:
过点作,交直线BD于点,连结.
由三棱台得,所以直线DF与平面DBC所成角等于直线CO与平面DBC所成角.
由平面得,故平面BCD,所以为直线CO与平面DBC所成角.
设.
由,得,
所以,
因此,直线DF与平面DBC所成角的正弦值为.
方法二:
由三棱台得,所以直线DF与平面DBC所成角等于直线CO与平面DBC所成角,记为.
如图,以为原点,分别以射线OC,OD为y,z轴的正半轴,建立空间直角坐标系.
设.
由题意知各点坐标如下:
.
因此.
设平面BCD的法向量.
由即,可取.
所以.
因此,直线DF与平面DBC所成角的正弦值为.
例4、【2020年高考全国Ⅱ卷理数】如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.
(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F;
(2)设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.
【解析】(1)因为M,N分别为BC,B1C1的中点,所以.又由已知得AA1∥CC1,故AA1∥MN.
因为△A1B1C1是正三角形,所以B1C1⊥A1N.又B1C1⊥MN,故B1C1⊥平面A1AMN.
所以平面A1AMN⊥平面.
(2)由已知得AM⊥BC.以M为坐标原点,的方向为x轴正方向,为单位长,建立空间直角坐标系M-xyz,则AB=2,AM=.
连接NP,则四边形AONP为平行四边形,故.由(1)知平面A1AMN⊥平面ABC,作NQ⊥AM,垂足为Q,则NQ⊥平面ABC.
设,则,
故.
又是平面A1AMN的法向量,故.
所以直线B1E与平面A1AMN所成角的正弦值为.
题型三、平面与平面所成的角
利用平面的法向量求二面角的大小时,当求出两半平面α,β的法向量n1,n2时,要根据观察判断向量在图形中的方向,从而确定二面角与向量n1,n2的夹角是相等还是互补,这是利用向量求二面角的难点、易错点
例5、【2019年高考全国Ⅱ卷理数】如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
【解析】(1)由已知得,平面,平面,
故.
又,所以平面.
(2)由(1)知.由题设知≌,所以,
故,.
以为坐标原点,的方向为x轴正方向,为单位长,建立如图所示的空间直角坐标系D–xyz,
则C(0,1,0),B(1,1,0),(0,1,2),E(1,0,1),,,.
设平面EBC的法向量为n=(x,y,x),则
即
所以可取n=.
设平面的法向量为m=(x,y,z),则
即
所以可取m=(1,1,0).
于是.
所以,二面角的正弦值为.
【名师点睛】本题考查了利用线面垂直的性质定理证明线线垂直以及线面垂直的判定,考查了利用空间向量求二角角的余弦值,以及同角的三角函数关系,考查了数学运算能力.
例6、【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B−CG−A的大小.
【答案】(1)见解析;(2).
【解析】(1)由已知得ADBE,CGBE,所以ADCG,故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得ABBE,ABBC,故AB平面BCGE.
又因为AB平面ABC,所以平面ABC平面BCGE.
(2)作EHBC,垂足为H.
因为EH平面BCGE,平面BCGE平面ABC,所以EH平面ABC.
由已知,菱形BCGE的边长为2,∠EBC=60°,可求得BH=1,EH=.
以H为坐标原点,的方向为x轴的正方向,建立如图所示的空间直角坐标系H–xyz,
则A(–1,1,0),C(1,0,0),G(2,0,),=(1,0,),=(2,–1,0).
设平面ACGD的法向量为n=(x,y,z),则
即
所以可取n=(3,6,–).
又平面BCGE的法向量可取为m=(0,1,0),
所以.
因此二面角B–CG–A的大小为30°.
例7、(2020届山东省潍坊市高三上期中)如图,在棱长均为的三棱柱中,平面平面,,为与的交点.
(1)求证:;
(2)求平面与平面所成锐二面角的余弦值.
【解析】
(1)因为四边形为菱形,所以,
又平面平面,平面平面,
所以平面,
因为平面,
所以.
(2)因为,所以菱形为正方形,
在中,,
在中,,,,
所以,,又,,
所以,平面;
以为坐标原点,以,,所在直线分别为轴,轴,轴,建立如图所示的空间直角坐标系.
,,,,
设平面的一个法向量为平面的一个法向量为,则
令,得,
令,得,
设平面与平面所成锐二面角为,
则,
所以平面与平面所成锐二面角的余弦值为.
二、达标训练
1、【2019年高考天津卷理数】如图,平面,,.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)若二面角的余弦值为,求线段的长.
【解析】依题意,可以建立以为原点,分别以的方向为轴,轴,轴正方向的空间直角坐标系(如图),可得,.设,则.
(1)依题意,是平面的法向量,又,可得,又因为直线平面,所以平面.
(2)依题意,.
设为平面的法向量,则即不妨令,
可得.因此有.
所以,直线与平面所成角的正弦值为.
(3)设为平面的法向量,则即
不妨令,可得.
由题意,有,解得.经检验,符合题意.
所以,线段的长为.
2、【2019年高考浙江卷】如图,已知三棱柱,平面平面,,分别是AC,A1B1的中点.
(1)证明:;
(2)求直线EF与平面A1BC所成角的余弦值.
【解析】方法一:
(1)连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC,A1E平面A1ACC1,
平面A1ACC1∩平面ABC=AC,
所以,A1E⊥平面ABC,则A1E⊥BC.
又因为A1F∥AB,∠ABC=90°,故BC⊥A1F.
所以BC⊥平面A1EF.
因此EF⊥BC.
(2)取BC中点G,连接EG,GF,则EGFA1是平行四边形.
由于A1E⊥平面ABC,故A1E⊥EG,所以平行四边形EGFA1为矩形.
由(1)得BC⊥平面EGFA1,则平面A1BC⊥平面EGFA1,
所以EF在平面A1BC上的射影在直线A1G上.
连接A1G交EF于O,则∠EOG是直线EF与平面A1BC所成的角(或其补角).
不妨设AC=4,则在Rt△A1EG中,A1E=2,EG=.
由于O为A1G的中点,故,
所以.
因此,直线EF与平面A1BC所成角的余弦值是.
方法二:
(1)连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC,A1E平面A1ACC1,
平面A1ACC1∩平面ABC=AC,所以,A1E⊥平面ABC.
如图,以点E为原点,分别以射线EC,EA1为y,z轴的正半轴,建立空间直角坐标系E–xyz.
不妨设AC=4,则
A1(0,0,2),B(,1,0),,,C(0,2,0).
因此,,.
由得.
(2)设直线EF与平面A1BC所成角为θ.
由(1)可得.
设平面A1BC的法向量为n,
由,得,
取n,故,
因此,直线EF与平面A1BC所成的角的余弦值为.
【名师点睛】本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力.
3、【2018年高考全国Ⅰ卷理数】如图,四边形为正方形,分别为的中点,以为折痕把折起,使点到达点的位置,且.
(1)证明:平面平面;
(2)求与平面所成角的正弦值.
【解析】方法一:(1)由已知可得,BF⊥PF,BF⊥EF,
所以BF⊥平面PEF.
又平面ABFD,
所以平面PEF⊥平面ABFD.
(2)在平面DEF中,过P作PH⊥EF于点H,连接DH,如图,
由于EF为平面ABCD和平面PEF的交线,PH⊥EF,
则PH⊥平面ABFD,故PH⊥DH.
则与平面所成的角为.
在三棱锥P-DEF中,可以利用等体积法求PH.
因为DE∥BF且PF⊥BF,所以PF⊥DE,
又△PDF≌△CDF,所以∠FPD=∠FCD=90°,
所以PF⊥PD,
由于DE∩PD=D,则PF⊥平面PDE,
故,
因为BF∥DA且BF⊥平面PEF,
所以DA⊥平面PEF,
所以DE⊥EP.
设正方形的边长为2a,则PD=2a,DE=a,
在△PDE中,,
所以,
故,
又,
所以,
所以在△PHD中,,
故与平面所成角的正弦值为.
方法二:(1)由已知可得,BF⊥PF,BF⊥EF,
所以BF⊥平面PEF.
又平面ABFD,
所以平面PEF⊥平面ABFD.
(2)作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.
以H为坐标原点,的方向为y轴正方向,为单位长,建立如图所示的空间直角坐标系H−xyz.
由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=.又PF=1,EF=2,故PE⊥PF.
可得.
则为平面ABFD的法向量.
设DP与平面ABFD所成角为,则.
所以DP与平面ABFD所成角的正弦值为.
4、(2020届山东省九校高三上学期联考)已知四棱柱的底面为菱形,,,,平面,.
(1)证明:平面;
(2)求钝二面角的余弦值.
【解析】
(1)证明:连接交于点,易知为中点,
∵为中点,∴在中,,
∵平面,平面,
∴平面.
(2)∵平面,∴,
∵且为的中点,
∴,
∵平面且,
∴平面,如图,建立空间直角坐标系.
易得:,,,,
∴,,
设平面的一个法向量为,
则,∴,
令,得,
∴.
同理可得平面的一个法向量为,
∴,
∴钝二面角的余弦值为.
5、(2020届山东省潍坊市高三上期末)在底面为正方形的四棱锥中,平面平面分别为棱和的中点.
(1)求证:平面;
(2)若直线与所成角的正切值为,求平面与平面所成锐二面角的大小.
【解析】
(1)证明:取的中点,连接,
因为分别为和的中点,四边形为正方形,
所以,
因为平面平面,
所以平面平面,
因为平面,
所以平面.
(2)因为平面平面,平面平面
平面
所以平面,
所以,
因为,
所以就是直线与所成的角,
所以,
设,
分别取和的中点,连,
因为,
所以,
因为平面平面,平面平面平面,
所以平面
如图,建立空间直角坐标系,
则,
所以,
设是平面的一个法向量,则
取,则,所以
是平面的一个法向量,
所以,
所以所求二面角的大小为
6、(2019南京、盐城一模)如图,四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=1,PA=AB=eq \r(2),点E是棱PB的中点.
(1) 求异面直线EC与PD所成角的余弦值;
(2) 求二面角BECD的余弦值.
规范解答 (1)因为PA⊥底面ABCD,且底面ABCD为矩形,所以AB,AD,AP两两垂直,以A为原点,AB,AD,AP分别为x,y,z轴建立空间直角坐标系.又因为PA=AB=eq \r(2),AD=1,所以A(0,0,0),B(eq \r(2),0,0),C(eq \r(2),1,0),D(0,1,0),P(0,0,eq \r(2)),(2分)
因为E是棱PB的中点,所以Eeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2),0,\f(\r(2),2))),
所以eq \(EC,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2),1,-\f(\r(2),2))),eq \(PD,\s\up6(→))=(0,1,-eq \r(2)),
所以cs〈eq \(EC,\s\up6(→)),eq \(PD,\s\up6(→))〉=eq \f(1+1,\r(\f(1,2)+1+\f(1,2))×\r(1+2))=eq \f(\r(6),3),
所以异面直线EC与PD所成角的余弦值为eq \f(\r(6),3).(6分)
(2)由(1)得eq \(EC,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2),1,-\f(\r(2),2))),eq \(BC,\s\up6(→))=(0,1,0),eq \(DC,\s\up6(→))=(eq \r(2),0,0).
设平面BEC的法向量为n1=(x1,y1,z1),所以eq \b\lc\{(\a\vs4\al\c1(\f(\r(2),2)x1+y1-\f(\r(2),2)z1=0,,y1=0.))
令x1=1,则z1=1,所以平面BEC的一个法向量为n1=(1,0,1).
设平面DEC的法向量为n2=(x2,y2,z2),所以eq \b\lc\{(\a\vs4\al\c1(\f(\r(2),2)x2+y2-\f(\r(2),2)z2=0,,\r(2)x2=0.))
令z2=eq \r(2),则y2=1,所以平面DEC的一个法向量为n2=(0,1,eq \r(2)),
所以cs〈n1,n2〉=eq \f(\r(2),\r(1+1)×\r(1+2))=eq \f(\r(3),3).由图可知二面角BECD为钝角,所以二面角BECD的余弦值为-eq \f(\r(3),3).(10分)
新高考数学专题复习专题22利用空间向量研究探索性与最值问题专题练习(学生版+解析): 这是一份新高考数学专题复习专题22利用空间向量研究探索性与最值问题专题练习(学生版+解析),共26页。试卷主要包含了题型选讲,最值问题等内容,欢迎下载使用。
新高考数学专题复习专题06函数单调性的综合运用专题练习(学生版+解析): 这是一份新高考数学专题复习专题06函数单调性的综合运用专题练习(学生版+解析),共14页。试卷主要包含了题型选讲, 给定区间的单调性等内容,欢迎下载使用。
新高考数学一轮复习精选考点专项突破题集专题5.3《运用空间向量解决立体几何中的角与距离》(含解析): 这是一份新高考数学一轮复习精选考点专项突破题集专题5.3《运用空间向量解决立体几何中的角与距离》(含解析),共30页。试卷主要包含了故选C,))等内容,欢迎下载使用。












