

所属成套资源:新高考数学之圆锥曲线综合讲义(原卷版+解析)
新高考数学之圆锥曲线综合讲义第9讲蒙日圆问题(原卷版+解析)
展开
这是一份新高考数学之圆锥曲线综合讲义第9讲蒙日圆问题(原卷版+解析),共29页。学案主要包含了解答题等内容,欢迎下载使用。
1.已知椭圆的一个焦点为,离心率为.
(1)求椭圆的标准方程;
(2)若动点为椭圆外一点,且点到椭圆的两条切线相互垂直,求点的轨迹方程.
2.给定椭圆C: (a>b>0),称圆心在原点O,半径为的圆为椭圆C的“准圆”.若椭圆C的一个焦点为F(,0),其短轴上的一个端点到F的距离为.
(1)求椭圆C的方程和其“准圆”方程;
(2)若点P是椭圆C的“准圆”上的动点,过点P作椭圆的切线l1,l2交“准圆”于点M,N.证明:l1⊥l2,且线段MN的长为定值.
3.给定椭圆 C : ,称圆心在原点,半径为的圆是椭圆 C 的“伴随圆”.若椭圆 C 的一个焦点为 F1(, 0) ,其短轴上的一个端点到 F1 的距离为
(1)求椭圆 C 的方程及其“伴随圆”方程;
(2)若倾斜角 45°的直线 l 与椭圆 C 只有一个公共点,且与椭圆 C 的伴随圆相交于 M .N 两点,求弦 MN 的的长;
(3)点 P 是椭圆 C 的伴随圆上一个动点,过点 P 作直线 l1、l2,使得 l1、l2与椭圆 C 都只有一个公共点,判断l1、l2的位置关系,并说明理由.
4.已知抛物线:(),圆:(),抛物线上的点到其准线的距离的最小值为.
(1)求抛物线的方程及其准线方程;
(2)如图,点是抛物线在第一象限内一点,过点P作圆的两条切线分别交抛物线于点A,B(A,B异于点P),问是否存在圆使AB恰为其切线?若存在,求出r的值;若不存在,说明理由.
5.已知椭圆:的长半轴长为,点(为椭圆的离心率)在椭圆上.
(1)求椭圆的标准方程;
(2)如图,为直线上任一点,过点椭圆上点处的切线为,,切点分别,,直线与直线,分别交于,两点,点,的纵坐标分别为,,求的值.
6.已知中心在原点的椭圆C1和抛物线C2有相同的焦点(1,0),椭圆C1过点,抛物线的顶点为原点.
(1)求椭圆C1和抛物线C2的方程;
(2)设点P为抛物线C2准线上的任意一点,过点P作抛物线C2的两条切线PA,PB,其中A、B为切点.
设直线PA,PB的斜率分别为k1,k2,求证:k1k2为定值;
②若直线AB交椭圆C1于C,D两点,S△PAB,S△PCD分别是△PAB,△PCD的面积,试问:是否有最小值?若有,求出最小值;若没有,请说明理由.
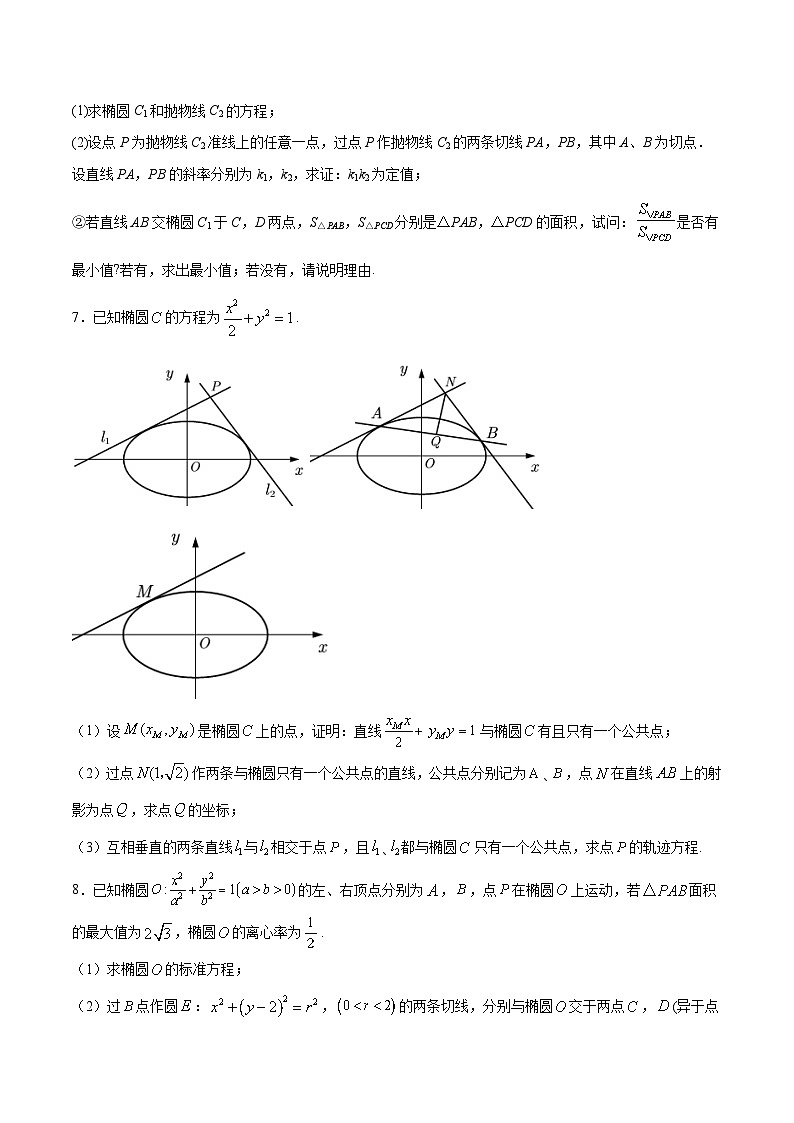
7.已知椭圆的方程为.
(1)设是椭圆上的点,证明:直线与椭圆有且只有一个公共点;
(2)过点作两条与椭圆只有一个公共点的直线,公共点分别记为、,点在直线上的射影为点,求点的坐标;
(3)互相垂直的两条直线与相交于点,且、都与椭圆只有一个公共点,求点的轨迹方程.
8.已知椭圆的左、右顶点分别为,,点在椭圆上运动,若面积的最大值为,椭圆的离心率为.
(1)求椭圆的标准方程;
(2)过点作圆:,的两条切线,分别与椭圆交于两点,(异于点),当变化时,直线是否恒过某定点?若是,求出该定点坐标,若不是,请说明理由.
9.如图,在平面直角坐标系xOy中,已知椭圆C1:+y2=1,椭圆C2:+=1(a>b>0),C2与C1的长轴长之比为∶1,离心率相同.
(1) 求椭圆C2的标准方程;
(2) 设点P为椭圆C2上的一点.
①射线PO与椭圆C1依次交于点A,B,求证:为定值;
②过点P作两条斜率分别为k1,k2的直线l1,l2,且直线l1,l2与椭圆C1均有且只有一个公共点,求证k1·k2为定值.
10.已知抛物线上一点到焦点的距离.
(1)求抛物线的方程;
(2)过点引圆的两条切线,切线与抛物线的另一交点分别为,线段中点的横坐标记为,求的取值范围.
11.如图,已知是椭圆:上的任一点,从原点向圆:作两条切线,分别交椭圆于点、.
(1)若直线,的斜率存在,并记为,,求证:为定值;
(2)试问是否为定值?若是,求出该值;若不是,说明理由.
12.已知抛物线E:过点,过抛物线E上一点作两直线PM,PN与圆C:相切,且分别交抛物线E于M、N两点.
(1)求抛物线E的方程,并求其焦点坐标和准线方程;
(2)若直线MN的斜率为,求点P的坐标.
第9讲 蒙日圆问题
一、解答题
1.已知椭圆的一个焦点为,离心率为.
(1)求椭圆的标准方程;
(2)若动点为椭圆外一点,且点到椭圆的两条切线相互垂直,求点的轨迹方程.
【答案】(1);(2).
【详解】
试题分析:(1)利用题中条件求出的值,然后根据离心率求出的值,最后根据、、三者的关系求出的值,从而确定椭圆的标准方程;(2)分两种情况进行计算:第一种是在从点所引的两条切线的斜率都存在的前提下,设两条切线的斜率分别为、,并由两条切线的垂直关系得到,并设从点所引的直线方程为,将此直线的方程与椭圆的方程联立得到关于的一元二次方程,利用得到有关的一元二次方程,最后利用以及韦达定理得到点的轨迹方程;第二种情况是两条切线与坐标轴垂直的情况下求出点的坐标,并验证点是否在第一种情况下所得到的轨迹上,从而得到点的轨迹方程.
(1)由题意知,且有,即,解得,
因此椭圆的标准方程为;
(2)①设从点所引的直线的方程为,即,
当从点所引的椭圆的两条切线的斜率都存在时,分别设为、,则,
将直线的方程代入椭圆的方程并化简得,
,
化简得,即,
则、是关于的一元二次方程的两根,则,
化简得;
②当从点所引的两条切线均与坐标轴垂直,则的坐标为,此时点也在圆上.
综上所述,点的轨迹方程为.
考点:本题以椭圆为载体,考查直线与圆锥曲线的位置关系以及动点的轨迹方程,将直线与二次曲线的公共点的个数利用的符号来进行转化,计算量较大,从中也涉及了方程思想的灵活应用.
2.给定椭圆C: (a>b>0),称圆心在原点O,半径为的圆为椭圆C的“准圆”.若椭圆C的一个焦点为F(,0),其短轴上的一个端点到F的距离为.
(1)求椭圆C的方程和其“准圆”方程;
(2)若点P是椭圆C的“准圆”上的动点,过点P作椭圆的切线l1,l2交“准圆”于点M,N.证明:l1⊥l2,且线段MN的长为定值.
【答案】(1)椭圆方程为,“准圆”方程为x2+y2=4;(2)证明见解析.
【分析】
(1)由已知,进而可得椭圆C的方程和其“准圆”方程;
(2)①当直线l1,l2中有一条斜率不存在时,分别求出l1和l2,验证命题成立;②当l1,l2斜率存在时,设点P(x0,y0),其中,联立过点P(x0,y0)与椭圆相切的直线方程与椭圆方程,由Δ=0化简整理,可证得l1⊥l2;进而得出线段MN为“准圆”x2+y2=4的直径,即线段MN的长为定值.
【详解】
(1)∵椭圆C的一个焦点为
其短轴上的一个端点到F的距离为.
∴,
∴,
∴椭圆方程为,
∴“准圆”方程为x2+y2=4.
(2)证明:①当直线l1,l2中有一条斜率不存在时,不妨设直线l1斜率不存在,则l1:x=±,
当l1:x=时,l1与“准圆”交于点(,1),(,-1),
此时l2为y=1(或y=-1),显然直线l1,l2垂直;
同理可证当l1:x=-时,直线l1,l2垂直.
②当l1,l2斜率存在时,
设点P(x0,y0),其中.
设经过点P(x0,y0)与椭圆相切的直线为
y=t(x-x0)+y0,
∴由
得(1+3t2)x2+6t(y0-tx0)x+3(y0-tx0)2-3=0.
由Δ=0化简整理,得(3-)t2+2x0y0t+1-=0,
∵,∴有(3-)t2+2x0y0t+(-3)=0.
设l1,l2的斜率分别为t1,t2,
∵l1,l2与椭圆相切,∴t1,t2满足上述方程(3-)t2+2x0y0t+(-3)=0,
∴t1·t2=-1,即l1,l2垂直.
综合①②知,l1⊥l2.
∵l1,l2经过点P(x0,y0),又分别交其“准圆”于点M,N,且l1,l2垂直.
∴线段MN为“准圆”x2+y2=4的直径,|MN|=4,
∴线段MN的长为定值.
【点睛】
思路点睛:本题考查椭圆的标准方程,考查新定义,考查椭圆的切线方程,考查直线与椭圆的位置关系,有关平面解析问题一些基本解题思想总结如下:
1.常规求值问题:需要找等式,范围问题需要找不等式;
2.是否存在问题:当作存在去求,不存在时会无解;
3.证明定值问题:把变动的元素用参数表示出来,然后证明结果与参数无关,也可先猜再证;
4.处理定点问题:把方程中参数的同次项集在一起,并令各项系数为,也可先猜再证;
5.最值问题:将对象表示为变量的函数求解.
3.给定椭圆 C : ,称圆心在原点,半径为的圆是椭圆 C 的“伴随圆”.若椭圆 C 的一个焦点为 F1(, 0) ,其短轴上的一个端点到 F1 的距离为
(1)求椭圆 C 的方程及其“伴随圆”方程;
(2)若倾斜角 45°的直线 l 与椭圆 C 只有一个公共点,且与椭圆 C 的伴随圆相交于 M .N 两点,求弦 MN 的的长;
(3)点 P 是椭圆 C 的伴随圆上一个动点,过点 P 作直线 l1、l2,使得 l1、l2与椭圆 C 都只有一个公共点,判断l1、l2的位置关系,并说明理由.
【答案】(1)椭圆方程:;伴随圆方程: x2 y2 1 ;(2) 2;(3)垂直,(斜率乘积为 1 ,分斜率存在与否)
【分析】
(1)直接由椭圆C的一个焦点为,其短轴上的一个端点到F1的距离为,求出,即可求椭圆C的方程及其“伴随圆”方程;
(2)先把直线方程与椭圆方程联立,利用对应的判别式为0求出,进而求出直线方程以及圆心到直线的距离;即可求弦MN的长;
(3)先对直线l1,l2的斜率是否存在分两种情况讨论,然后对每一种情况中的直线l1,l2与椭圆C都只有一个公共点进行求解即可证:l1⊥l2.(在斜率存在时,是先设直线方程,把直线与椭圆方程联立,利用斜率为对应方程的根来判断结论).
【详解】
解:(1)因为,所以b=1
所以椭圆的方程为,
伴随圆的方程为x2+y2=4.
(2)设直线l的方程y=x+b,由得4x2+6bx+3b2﹣3=0
由△=(6b)2﹣16(3b2﹣3)=0得b2=4
圆心到直线l的距离为
所以
(3)①当l1,l2中有一条无斜率时,不妨设l1无斜率,
因为l1与椭圆只有一个公共点,则其方程为或,
当l1方程为时,此时l1与伴随圆交于点,
此时经过点(或且与椭圆只有一个公共点的直线是y=1(或y=﹣1),
即l2为y=1(或y=﹣1),显然直线l1,l2垂直;
同理可证l1方程为时,直线l1,l2垂直.
②当l1,l2都有斜率时,设点P(x0,y0),其中x02+y02=4,
设经过点P(x0,y0),与椭圆只有一个公共点的直线为y=k(x﹣x0)+y0,
由,消去y得到x2+3(kx+(y0﹣kx0))2﹣3=0,
即(1+3k2)x2+6k(y0﹣kx0)x+3(y0﹣kx0)2﹣3=0,
△=[6k(y0﹣kx0)]2﹣4•(1+3k2)[3(y0﹣kx0)2﹣3]=0,
经过化简得到:(3﹣x02)k2+2x0y0k+1﹣y02=0,
因为x02+y02=4,所以有(3﹣x02)k2+2x0y0k+(x02﹣3)=0,
设l1,l2的斜率分别为k1,k2,因为l1,l2与椭圆都只有一个公共点,
所以k1,k2满足方程(3﹣x02)k2+2x0y0k+(x02﹣3)=0,
因而k1•k2=﹣1,即l1,l2垂直.
【点睛】
本题主要考查椭圆的方程和几何性质,直线的方程,两点间的距离公式以及点到直线的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力.
4.已知抛物线:(),圆:(),抛物线上的点到其准线的距离的最小值为.
(1)求抛物线的方程及其准线方程;
(2)如图,点是抛物线在第一象限内一点,过点P作圆的两条切线分别交抛物线于点A,B(A,B异于点P),问是否存在圆使AB恰为其切线?若存在,求出r的值;若不存在,说明理由.
【答案】(1)的方程为,准线方程为.(2)存在,
【分析】
(1)由得到p即可;
(2)设,利用点斜式得到PA的的方程为,由到PA的距离为半径可得,同理,同理写出直线AB的方程,利用点到直线AB的距离为半径建立方程即可.
【详解】
解:(1)由题意得,解得,
所以抛物线的方程为,准线方程为.
(2)由(1)知,.
假设存在圆使得AB恰为其切线,设,,
则直线PA的的方程为,即.
由点到PA的距离为r,得,
化简,得,
同理,得.
所以,是方程的两个不等实根,
故,.
易得直线AB的方程为,
由点到直线AB的距离为r,得,
所以,
于是,,
化简,得,即.
经分析知,,因此.
【点睛】
本题主要考查抛物线的定义和几何性质,直线与圆、抛物线的位置关系等,考查运算求解能力、数形结合思想.
5.已知椭圆:的长半轴长为,点(为椭圆的离心率)在椭圆上.
(1)求椭圆的标准方程;
(2)如图,为直线上任一点,过点椭圆上点处的切线为,,切点分别,,直线与直线,分别交于,两点,点,的纵坐标分别为,,求的值.
【答案】(1);(2).
【分析】
(1)因为点在椭圆上,所以,然后,利用,,得出,进而求解即可
(2)设点的坐标为,直线的方程为,直线的方程为,分别联立方程:和,利用韦达定理,再利用,,即可求出的值
【详解】
(1)由椭圆的长半轴长为,得.
因为点在椭圆上,所以.
又因为,,所以,
所以(舍)或.
故椭圆的标准方程为.
(2)设点的坐标为,直线的方程为,直线的方程为.
据得.
据题意,得,得,
同理,得,
所以.
又可求,得,,
所以
.
【点睛】
本题考查椭圆标准方程的求解以及联立方程求定值的问题,联立方程求定值的关键在于利用韦达定理进行消参,属于中档题
6.已知中心在原点的椭圆C1和抛物线C2有相同的焦点(1,0),椭圆C1过点,抛物线的顶点为原点.
(1)求椭圆C1和抛物线C2的方程;
(2)设点P为抛物线C2准线上的任意一点,过点P作抛物线C2的两条切线PA,PB,其中A、B为切点.
设直线PA,PB的斜率分别为k1,k2,求证:k1k2为定值;
②若直线AB交椭圆C1于C,D两点,S△PAB,S△PCD分别是△PAB,△PCD的面积,试问:是否有最小值?若有,求出最小值;若没有,请说明理由.
【答案】(1) 抛物线的标准方程为,椭圆的方程为:,(2)①证明见解析,②有,最小值为
【分析】
(1)利用可得抛物线的标准方程,根据和点在椭圆上列方程组可求得和,从而可得标准方程;
(2)①利用△=0以及韦达定理可得结论;
②先求出直线过定点,将问题转化为,即求得最小值,当直线的斜率存在时,联立直线与抛物线,利用弦长公式求出和,然后求比值,此时大于,当直线的斜率不存在时,直接求出和可得比值为.从而可得结论.
【详解】
(1)因为抛物线C2有相同的焦点(1,0),且顶点为原点,所以,所以,
所以抛物线的标准方程为,
设椭圆方程为,则且,解得,
所以椭圆的方程为:.
(2)①证明:设,过点与抛物线相切的直线为,
由,消去得,
由△=,得,
则.
②设
由①得,则,
所以直线的方程为,所以,
即,即直线恒过定点,
设点到直线的距离为,
所以,
当直线的斜率存在时,设直线的方程为,
设,
由,消去得,
时,△恒成立,
,
由消去得,△恒成立,
则
.
所以,
当直线的斜率不存在时,直线的方程为,
此时,,,
所以的最小值为.
【点睛】
本题考查了求抛物线和椭圆的标准方程,考查了直线与抛物线相切,考查了直线与椭圆相交的问题,考查了三角形的面积公式,考查了分类讨论思想,考查了弦长公式,属于难题.
7.已知椭圆的方程为.
(1)设是椭圆上的点,证明:直线与椭圆有且只有一个公共点;
(2)过点作两条与椭圆只有一个公共点的直线,公共点分别记为、,点在直线上的射影为点,求点的坐标;
(3)互相垂直的两条直线与相交于点,且、都与椭圆只有一个公共点,求点的轨迹方程.
【答案】(1)证明见解析;(2);(3).
【分析】
(1)当时,符合题意;当时,联立直线与椭圆的方程,得判别式为0,从而方程组只有一组解,进而可得答案;
(2)设,,得出A,B的坐标满足直线方程,推出直线AB的方程为,联立NQ的方程解得Q点坐标;
(3)设,分两种情况:当直线与有一条斜率不存在时,当直线与有一条斜率存在时,讨论点P的轨迹,即可得出答案.
【详解】
(1)当时,,直线,
即直线,与椭圆只有一个公共点.
当时,由得,,又,
有,从而方程组只有一组解,
直线与椭圆的有且只有一个公共点.
(2)设,.
由(1)知两条直线为,,
又是它们的交点,,,
从而有,的坐标满足直线方程,
所以直线:.
直线的方程为,
由解得,即,
(3)设.
当直线与有一条斜率不存在时,,.
当直线与的斜率都存在时,设为和,
由得,
由,
整理得,,和是这个方程的两个根,
有,得,
所以点的轨迹方程是.
【点睛】
关键点点睛:解决第一问主要是通过联立直线与椭圆所构成的方程组有一个解;解决第二问主要是通过第一问中的结论得出的方程;解决第三问主要是依据两直线的关系得到.
8.已知椭圆的左、右顶点分别为,,点在椭圆上运动,若面积的最大值为,椭圆的离心率为.
(1)求椭圆的标准方程;
(2)过点作圆:,的两条切线,分别与椭圆交于两点,(异于点),当变化时,直线是否恒过某定点?若是,求出该定点坐标,若不是,请说明理由.
【答案】(1);(2)直线恒过定点.
【分析】
(1)首先列出关于的等式,再求椭圆的标准方程;(2)首先设出过点的切线方程,利用,得到关于斜率的一元二次方程,得到根与系数的关系,再与椭圆方程联立求得点的坐标,写出直线的斜率,并写出直线的方程,说明直线过定点.
【详解】
(1)由题可知当点在椭圆的上顶点时,最大,
此时,∴,,,
∴椭圆的标准方程为.
(2)设过点与圆相切的直线方程为,即,
∵直线与圆:相切,∴,
即得.
设两切线的斜率分别为,,则,
设,,由,
∴,即,∴;
同理:,;
∴,
∴直线的方程为.
整理得,
∴直线恒过定点.
【点睛】
本题考查椭圆方程,直线与圆,直线与椭圆的位置关系,重点考查转化思想,计算能力,逻辑推理能力,属于难题.
9.如图,在平面直角坐标系xOy中,已知椭圆C1:+y2=1,椭圆C2:+=1(a>b>0),C2与C1的长轴长之比为∶1,离心率相同.
(1) 求椭圆C2的标准方程;
(2) 设点P为椭圆C2上的一点.
①射线PO与椭圆C1依次交于点A,B,求证:为定值;
②过点P作两条斜率分别为k1,k2的直线l1,l2,且直线l1,l2与椭圆C1均有且只有一个公共点,求证k1·k2为定值.
【答案】(1)+=1;(2)①证明见解析,②证明见解析
【分析】
(1)根据已知条件,求出a,b的值,得到椭圆C2的标准方程.
(2)①对直线OP斜率分不存在和存在两种情况讨论,当OP斜率存在时,设直线OP的方程为y=kx,并与椭圆C1的方程联立,解得点A横坐标,同理求得点P横坐标,再通过弦长公式,求出的表达式,化简整理得到定值.
②设P(x0,y0),写出直线l1的方程,并与椭圆C1联立,得到关于x的一元二次方程,根据直线l1与椭圆C1有且只有一个公共点,得到方程只有一解,即Δ=0,整理得-2x0y0k1+-1=0,同理得到-2x0y0k2+-1=0,从而说明k1,k2是关于k的一元二次方程的两个根,运用根与系数的关系,证得定值.
【详解】
(1)设椭圆C2的焦距为2c,由题意,a=2,,解得b=,
因此椭圆C2的标准方程为+=1.
(2)①1°当直线OP斜率不存在时,
PA=-1,PB=+1,则==3-2.
2°当直线OP斜率存在时,设直线OP的方程为y=kx,代入椭圆C1的方程,消去y,得(4k2+1)x2=4,
所以,同理.
所以,由题意,xP与xA同号,所以xP=xA,
从而====3-2.
所以=3-2为定值.
②设P(x0,y0),所以直线l1的方程为y-y0=k1(x-x0),即y=k1x-k1x0+y0,
记t=-k1x0+y0,则l1的方程为y=k1x+t,
代入椭圆C1的方程,消去y,得(4+1)x2+8k1tx+4t2-4=0,
因为直线l1与椭圆C1有且只有一个公共点,
所以Δ=(8k1t)2-4(4+1)(4t2-4)=0,即4-t2+1=0,
将t=-k1x0+y0代入上式,整理得,-2x0y0k1+-1=0,
同理可得,-2x0y0k2+-1=0,
所以k1,k2为关于k的方程(-4)k2-2x0y0k+y-1=0的两根,从而k1·k2=.
又点在P(x0,y0)椭圆C2:+=1上,所以,
所以k1·k2=为定值.
【点睛】
本题考查求椭圆标准方程,考查椭圆中的定值问题,椭圆中的定值问题,一种方法是直接计算,即由直线与椭圆相交求出交点坐标,求出直线斜率等,然后计算题中要证定值的量即可得,一种不直接计算,像本题(2)②中通过直线与椭圆相切,得出两直线斜率满足的关系式,从而确定这两个斜率是某个二次方程的根,由韦达定理直接得证,即建立参数之间的联系,然后推导出定值.
10.已知抛物线上一点到焦点的距离.
(1)求抛物线的方程;
(2)过点引圆的两条切线,切线与抛物线的另一交点分别为,线段中点的横坐标记为,求的取值范围.
【答案】(1)(2)见解析
【分析】
(1)由题意确定p的值即可确定抛物线方程;
(2)很明显切线斜率存在,由圆心到直线的距离等于半径可得是方程的两根,联立直线方程与抛物线方程可得点的横坐标 .结合韦达定理将原问题转化为求解函数的值域的问题即可.
【详解】
(1)由抛物线定义,得,由题意得:
解得
所以,抛物线的方程为.
(2)由题意知,过引圆的切线斜率存在,设切线的方程为,则圆心到切线的距离,整理得,.
设切线的方程为,同理可得.
所以,是方程的两根,.
设,由得,,
由韦达定理知,,所以,同理可得.
设点的横坐标为,则
.
设,则,
所以,,对称轴,所以
【点睛】
本题主要考查抛物线方程的求解,直线与抛物线的位置关系等知识,意在考查学生的转化能力和计算求解能力.
11.如图,已知是椭圆:上的任一点,从原点向圆:作两条切线,分别交椭圆于点、.
(1)若直线,的斜率存在,并记为,,求证:为定值;
(2)试问是否为定值?若是,求出该值;若不是,说明理由.
【答案】(1)见解析;(2)为定值.
【解析】
试题分析:(1)设直线的直线方程分别为、,由圆心到直线的距离等于半径可以得到、,由此可得是方程的两个不相等的实数根,由违达定理可知,由点在椭圆上可得;(2)分直线与直线与椭圆方程联立,可得,,直接计算,并将代入表达式即可得到的和为定值.
试题解析:(1)因为直线:以及:与圆相切,
所以 ,
化简得:
同理:,
所以,
因为点在椭圆C上,所以,即,
所以 .
(2)是定值,定值为9.
理由如下:
法一:(i)当直线、不落在坐标轴上时,设,
联立解得
所以,同理,得,
由,
所以
(ii)当直线、落在坐标轴上时,显然有,
综上:
法二:(i)当直线、不落在坐标轴上时,设,
因为,所以,
因为在椭圆C上,所以, 即 ,
所以,整理得,
所以,所以.
(ii)当直线、落在坐标轴上时,显然有,
综上:.
考点:1.椭圆的定义与几何性质;2.直线与圆的位置关系;3.直线与椭圆的位置关系.
12.已知抛物线E:过点,过抛物线E上一点作两直线PM,PN与圆C:相切,且分别交抛物线E于M、N两点.
(1)求抛物线E的方程,并求其焦点坐标和准线方程;
(2)若直线MN的斜率为,求点P的坐标.
【答案】(1)抛物线E的方程为,焦点坐标为,准线方程为;(2)或
【分析】
(1)将点代入抛物线方程,可求出抛物线E的方程,进而可求出焦点坐标及准线方程;
(2)设,,可表示出直线及的斜率的表达式,进而可表示出两直线的方程,再结合直线和圆相切,利用点到直线的距离等于半径,可得,满足方程,从而得到,又直线MN的斜率为,可求出的值,即可求出点P的坐标.
【详解】
(1)将点代入抛物线方程得,,所以抛物线E的方程为,焦点坐标为:,准线方程为:.
(2)由题意知,,设,,
则直线的斜率为,同理,直线PN的斜率为,
直线MN的斜率为,故,
于是直线的方程为,即,
由直线和圆相切,得,
即,
同理,直线PN的方程为,
可得,
故,是方程的两根.
故,即,
所以,解得或.
当时,;当时,.
故点P的坐标为或.
【点睛】
本题考查抛物线方程的求法,考查直线与圆位置关系的应用,考查直线的方程,考查学生的计算求解能力,属于中档题.
相关学案
这是一份新高考数学之圆锥曲线综合讲义第11讲阿基米德三角形问题(原卷版+解析),共33页。学案主要包含了解答题等内容,欢迎下载使用。
这是一份新高考数学之圆锥曲线综合讲义第8讲角度问题(原卷版+解析),共24页。学案主要包含了解答题等内容,欢迎下载使用。
这是一份新高考数学之圆锥曲线综合讲义第7讲共线问题(原卷版+解析),共37页。学案主要包含了解答题等内容,欢迎下载使用。









