高考数学一轮复习讲练测(新教材新高考)专题9.6直线与圆锥曲线专题练习（学生版+解析）

这是一份高考数学一轮复习讲练测(新教材新高考)专题9.6直线与圆锥曲线专题练习（学生版+解析），共32页。试卷主要包含了已知直线，故所求的抛物线焦点为，等内容，欢迎下载使用。
1．（2021·四川成都市·成都七中高三月考（文））已知点是抛物线的焦点，点为抛物线的对称轴与其准线的交点，过作抛物线的切线，切点为，若点恰在以、为焦点的双曲线上，则双曲线的离心率为（ ）
A．B．
C．D．
2．（2022·全国高三专题练习）直线4kx－4y－k＝0与拋物线y2＝x交于A、B两点，若|AB|＝4，则弦AB的中点到直线x＋＝0的距离等于（ ）
A．B．C．D．
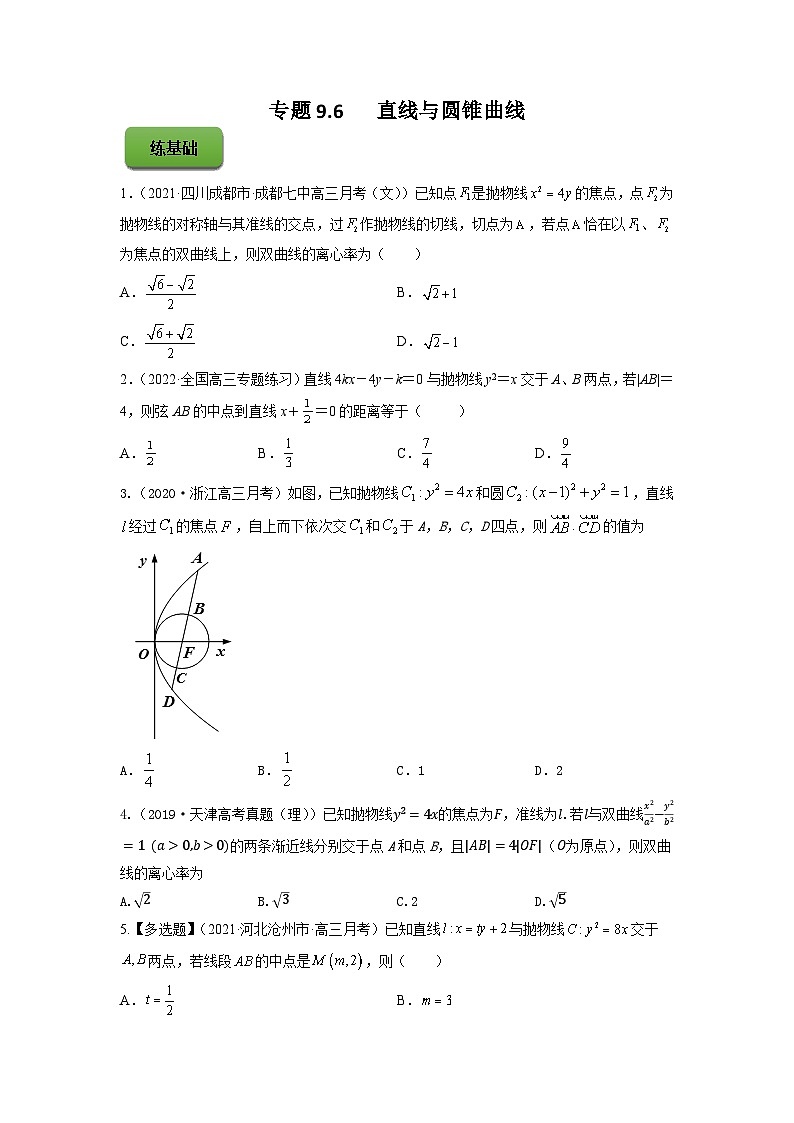
3.（2020·浙江高三月考）如图，已知抛物线和圆，直线经过的焦点，自上而下依次交和于A，B，C，D四点，则的值为
A．B．C．1D．2
4.（2019·天津高考真题（理））已知抛物线y2=4x的焦点为F，准线为l.若l与双曲线x2a2−y2b2=1 (a>0,b>0)的两条渐近线分别交于点A和点B，且|AB|=4|OF|（O为原点），则双曲线的离心率为
A.2B.3C.2D.5
5.【多选题】（2021·河北沧州市·高三月考）已知直线与抛物线交于两点，若线段的中点是，则（ ）
A．B．
C．D．点在以为直径的圆内
6．（2021·江苏扬州·高三月考）直线过抛物线的焦点F，且与C交于A，B两点，则___________.
7．（2022·全国高三专题练习）在直角坐标系xOy中，直线l过抛物线y2＝4x的焦点F，且与该抛物线相交于A、B两点，其中点A在x轴上方．若直线l的倾斜角为60°，则△OAF的面积为________．
8．（2022·全国高三专题练习）抛物线的焦点F是圆x2＋y2－4x＝0的圆心．
（1）求该抛物线的标准方程；
（2）直线l的斜率为2，且过抛物线的焦点，若l与抛物线、圆依次交于A、B、C、D，求|AB|＋|CD|．
9. （2020·广西钦州·高二期末（文））已知抛物线的顶点为，焦点坐标为．
（1）求抛物线方程；
（2）过点且斜率为1的直线与抛物线交于，两点，求线段的值．
10.（2021·江苏扬州·高三月考）在平面直角坐标系中，已知椭圆（）的右焦点为，离心率为.
（1）求椭圆C的标准方程；
（2）若过点F的直线l交C于A，B两点，线段的中点为M，分别过A，B作C的切线，，且与交于点P，证明：O，P，M三点共线.
练提升TIDHNEG
1.【多选题】（2021·山东济南·高三月考）已知直线过抛物线的焦点，且直线与抛物线交于两点，过两点分别作抛物线的切线，两切线交于点，设，， .则下列选项正确的是（ ）
A．
B．以线段为直径的圆与直线相离
C．当时，
D．面积的取值范围为
2.（2019·全国高三月考（文））已知抛物线的焦点为F，直线与抛物线交于M，N两点，且以线段MN为直径的圆过点F，则p=（ ）
A.1B.2C.4D.6
3．（2020·山西运城·高三月考（理））已知抛物线的焦点为，为坐标原点，点在抛物线上，且，点是抛物线的准线上的一动点，则的最小值为（ ）.
A．B．C．D．
4．（2021·重庆北碚区·西南大学附中高三月考）已知分别为双曲线的左、右焦点，过的直线与双曲线的右支交于两点，记的内切圆的半径为，的内切圆的半径为，圆、的面积为、，则的取值范围是__________．
5．（2020·山东青岛·高三开学考试）已知直线：与抛物线：在第一象限的交点为，过的焦点，，则抛物线的准线方程为_______；_______.
6．（2020·江苏如皋·高二月考）已知是抛物线的焦点，，为抛物线上任意一点，的最小值为，则________；若过的直线交抛物线于、两点，有，则________.
7．（2021·天津南开区·南开中学高三月考）设椭圆：的左焦点为，离心率为，过点且与轴垂直的直线被椭圆截得的线段长为．
（1）求椭圆的方程；
（2）设，分别为椭圆的左、右顶点，过点且斜率为的直线与椭圆交于点，两点，且，求的值．
8．（2021·北京）在平面直角坐标系xOy中，抛物线C的焦点在y轴上，且抛物线上的点P(x0,4)到焦点F的距离为5.斜率为2的直线l与抛物线C交于A，B两点.
（1）求抛物线C的标准方程，及抛物线在P点处的切线方程；
（2）若AB的垂直平分线分别交y轴和抛物线于M，N两点（M，N位于直线l两侧），当四边形AMBN为菱形时，求直线l的方程.
9. （2019·天津高考真题（文）） 设椭圆的左焦点为，左顶点为，上顶点为B.已知（为原点）.
（Ⅰ）求椭圆的离心率；
（Ⅱ）设经过点且斜率为的直线与椭圆在轴上方的交点为，圆同时与轴和直线相切，圆心在直线上，且，求椭圆的方程.
10．（2019·全国高三月考（理））如图，己知抛物线，直线交抛物线于两点，是抛物线外一点，连接分别交地物线于点，且.
（1）若，求点的轨迹方程.
（2）若，且平行x轴，求面积.
练真题TIDHNEG
1. （2021·天津高考真题）已知双曲线的右焦点与抛物线的焦点重合，抛物线的准线交双曲线于A，B两点，交双曲线的渐近线于C、D两点，若．则双曲线的离心率为（ ）
A．B．C．2D．3
2.（2020·全国高考真题（理））已知F为双曲线的右焦点，A为C的右顶点，B为C上的点，且BF垂直于x轴.若AB的斜率为3，则C的离心率为______________.
3.（2019·浙江高考真题）已知椭圆的左焦点为，点在椭圆上且在轴的上方，若线段的中点在以原点为圆心，为半径的圆上，则直线的斜率是_______.
4.（2020·全国高考真题（文））已知椭圆的离心率为，，分别为的左、右顶点．
（1）求的方程；
（2）若点在上，点在直线上，且，，求的面积．
5．（2019·江苏高考真题）如图，在平面直角坐标系xOy中，椭圆C:的焦点为F1（–1、0），F2（1，0）．过F2作x轴的垂线l，在x轴的上方，l与圆F2:交于点A，与椭圆C交于点D.连结AF1并延长交圆F2于点B，连结BF2交椭圆C于点E，连结DF1．已知DF1=．
（1）求椭圆C的标准方程；
（2）求点E的坐标．
6．（2021·山东高考真题）已知抛物线的顶点是坐标原点，焦点在轴的正半轴上，是抛物线上的点，点到焦点的距离为1，且到轴的距离是．
（1）求抛物线的标准方程；
（2）假设直线通过点，与抛物线相交于，两点，且，求直线的方程．
专题9.6 直线与圆锥曲线
练基础
1．（2021·四川成都市·成都七中高三月考（文））已知点是抛物线的焦点，点为抛物线的对称轴与其准线的交点，过作抛物线的切线，切点为，若点恰在以、为焦点的双曲线上，则双曲线的离心率为（ ）
A．B．
C．D．
【答案】B
【分析】
设切线方程为，将该直线的方程与抛物线的方程联立，由可求得的值，设点，利用韦达定理求出的值，利用双曲线的定义求出的值，进而可求得该双曲线的离心率.
【详解】
抛物线的焦点为，易知点，
设切线方程为，联立，即，
则，解得，设点，由韦达定理可得，
以、为焦点的双曲线的实轴长为，
则，则，
因此，该双曲线的离心率为，
故选：B.
2．（2022·全国高三专题练习）直线4kx－4y－k＝0与拋物线y2＝x交于A、B两点，若|AB|＝4，则弦AB的中点到直线x＋＝0的距离等于（ ）
A．B．C．D．
【答案】D
【分析】
分析可得直线恒过抛物线的焦点，根据抛物线焦点弦的性质|AB|＝x1＋x2，可得弦AB的中点的横坐标是，即得解
【详解】
直线4kx－4y－k＝0，即y＝k，
即直线4kx－4y－k＝0过拋物线y2＝x的焦点．
设A(x1，y1)，B(x2，y2)，
则|AB|＝x1＋x2，故x1＋x2＝，则弦AB的中点的横坐标是，
所以弦AB的中点到直线x＋＝0的距离是．
故选：D
3.（2020·浙江高三月考）如图，已知抛物线和圆，直线经过的焦点，自上而下依次交和于A，B，C，D四点，则的值为
A．B．C．1D．2
【答案】C
【解析】
因为抛物线的焦点为，
又直线经过的焦点，设直线，
由得，
设，则
由题意可得：，
同理，
所以.
故选C
4.（2019·天津高考真题（理））已知抛物线y2=4x的焦点为F，准线为l.若l与双曲线x2a2−y2b2=1 (a>0,b>0)的两条渐近线分别交于点A和点B，且|AB|=4|OF|（O为原点），则双曲线的离心率为
A.2B.3C.2D.5
【答案】D
【解析】
抛物线y2=4x的准线l的方程为x=−1，
双曲线的渐近线方程为y=±bax，
则有A(−1,ba),B(−1,−ba)
∴AB=2ba，2ba=4，b=2a，
∴e=ca=a2+b2a=5.
故选D.
5.【多选题】（2021·河北沧州市·高三月考）已知直线与抛物线交于两点，若线段的中点是，则（ ）
A．B．
C．D．点在以为直径的圆内
【答案】AB
【分析】
直线与抛物线方程联立，利用韦达定理和中点坐标可构造方程求得，知A正确；
将中点坐标代入直线方程即可求得，知B正确；
根据直线过抛物线焦点，根据抛物线焦点弦长公式可知C错误；
根据长度关系可确定，由此可确定D错误.
【详解】
对于A，设，，
由得：，，
又线段的中点为，，解得：，A正确；
对于B，在直线上，，B正确；
对于C，过点，为抛物线的焦点，
，C错误；
对于D，设，则，又，
，，在以为直径的圆上，D错误.
故选：AB.
6．（2021·江苏扬州·高三月考）直线过抛物线的焦点F，且与C交于A，B两点，则___________.
【答案】8
【分析】
由题意，求出，然后联立直线与抛物线方程，由韦达定理及即可求解.
【详解】
解：因为抛物线的焦点坐标为，
又直线过抛物线的焦点F，
所以，抛物线的方程为，
由，得，所以，
所以.
故答案为：8.
7．（2022·全国高三专题练习）在直角坐标系xOy中，直线l过抛物线y2＝4x的焦点F，且与该抛物线相交于A、B两点，其中点A在x轴上方．若直线l的倾斜角为60°，则△OAF的面积为________．
【答案】
【分析】
根据焦点坐标和直线的倾斜角得出直线的点斜式方程，然后利用直线和抛物线相交可得出A点坐标.继而可求出.
【详解】
解：由题意得：抛物线交点，直线l的倾斜角为60°
，直线l的方程为，即
代入抛物线方程，得
解得（舍去）
所以，于是可得
故答案为：
8．（2022·全国高三专题练习）抛物线的焦点F是圆x2＋y2－4x＝0的圆心．
（1）求该抛物线的标准方程；
（2）直线l的斜率为2，且过抛物线的焦点，若l与抛物线、圆依次交于A、B、C、D，求|AB|＋|CD|．
【答案】（1）y2＝8x；（2）6.
【分析】
（1）由圆的方程写出圆心坐标，进而可得抛物线方程.
（2）由题意知|AB|＋|CD|＝|AD|－|BC|，写出直线l的方程，设A(x1,y1)、D(x2,y2)，联立抛物线求x1＋x2、x1x2，即可求|AD|，进而求|AB|＋|CD|．
【详解】
（1）由圆的方程知：圆心坐标为(2,0)．故所求的抛物线焦点为(2,0)，
∴抛物线的标准方程为y2＝8x．
（2）如图，|AB|＋|CD|＝|AD|－|BC|，又|BC|＝4，只需求出|AD|即可．
由题意，AD所在直线方程为y＝2(x－2)，与抛物线方程y2＝8x联立得：x2－6x＋4＝0，
设A(x1,y1)，D(x2,y2)，则x1＋x2＝6，x1x2＝4，
∴|AD|＝|AF|＋|DF|＝(x1＋2)＋(x2＋2)＝x1＋x2＋4＝6＋4＝10，
∴|AB|＋|CD|＝|AD|－|BC|＝6．
9. （2020·广西钦州·高二期末（文））已知抛物线的顶点为，焦点坐标为．
（1）求抛物线方程；
（2）过点且斜率为1的直线与抛物线交于，两点，求线段的值．
【答案】（1）．（2）
【解析】
（1）∵焦点坐标为
∴，，
∴抛物线的方程为．
（2）设直线方程为，设，，
联立
消元得，
∴，，，
∴
．
∴线段的值为．
10.（2021·江苏扬州·高三月考）在平面直角坐标系中，已知椭圆（）的右焦点为，离心率为.
（1）求椭圆C的标准方程；
（2）若过点F的直线l交C于A，B两点，线段的中点为M，分别过A，B作C的切线，，且与交于点P，证明：O，P，M三点共线.
【答案】（1）；（2）证明见解析.
【分析】
（1）根据离心率及焦点求出即可得椭圆标准方程；
（2）设直线l的方程为：，联立方程后结合根与系数的关系计算即可证明三点共线.
【详解】
（1），椭圆方程为.
（2）由题意知斜率不为0，设直线l的方程为：，，，，，
由，
即.
，，
.
直线的方程为：①，
直线的方程为②，
，
，
，
，即O，P，M三点共线.
练提升TIDHNEG
1.【多选题】（2021·山东济南·高三月考）已知直线过抛物线的焦点，且直线与抛物线交于两点，过两点分别作抛物线的切线，两切线交于点，设，， .则下列选项正确的是（ ）
A．
B．以线段为直径的圆与直线相离
C．当时，
D．面积的取值范围为
【答案】BCD
【分析】
求出抛物线的焦点及准线，设直线l的方程为，与抛物线方程联立，利用韦达定理，计算可判断A；
利用定义及直线与圆的位置可判断B；由向量共线求出弦长判断C；求出点G的坐标及面积的函数式即可判断作答.
【详解】
抛物线的焦点，准线方程为，设直线l的方程为，
由消去y得：，于是得，
，A不正确；
以线段AB为直线的圆的圆心，则，点
到直线距离，
由抛物线定义得，显然，即以线段为直径的圆与直线相离，B正确；
当时，有，即，而，于是得，，C正确；
由求导得，于是得抛物线C在A处切线方程为：，即，
同理，抛物线C在B处切线方程为：，联立两切线方程解得，，
点到直线l：的距离，
于是得面积，当且仅当时取“=”，
面积的取值范围为，D正确.
故选：BCD
2.（2019·全国高三月考（文））已知抛物线的焦点为F，直线与抛物线交于M，N两点，且以线段MN为直径的圆过点F，则p=（ ）
A.1B.2C.4D.6
【答案】B
【解析】
设，
联立，消去x得，
由韦达定理可得：，
，
以线段MN为直径的圆的方程为，又其过点F，
，
，
，
，
故选：B
3．（2020·山西运城·高三月考（理））已知抛物线的焦点为，为坐标原点，点在抛物线上，且，点是抛物线的准线上的一动点，则的最小值为（ ）.
A．B．C．D．
【答案】A
【解析】
抛物线的准线方程为，
，到准线的距离为2，故点纵坐标为1，
把代入抛物线方程可得．
不妨设在第一象限，则，
点关于准线的对称点为，连接，
则，于是
故的最小值为．
故选：A．
4．（2021·重庆北碚区·西南大学附中高三月考）已知分别为双曲线的左、右焦点，过的直线与双曲线的右支交于两点，记的内切圆的半径为，的内切圆的半径为，圆、的面积为、，则的取值范围是__________．
【答案】
【分析】
首先根据双曲线以及切线性质证明轴，然后根据三角形相似关系求出与之间的关系，再根据已知条件求出的取值范围，进而求出的取值范围，最后利用函数思想求出的取值范围即可求解.
【详解】
由双曲线的方程可知，实半轴长，虚半轴长，且，
设圆与分别切于，，，连接，如下图所示：
由圆的切线性质可知，，，，
有双曲线定义可知，，即，
设，故，解得，，
由切线性质可知，与点坐标都为，
同理可知，圆也与轴也切于点，故轴，且、、三点共线，
又由三角形内切圆的性质可知，、分别为和的角平分线，
易得，，
从而可得，，故，
因为，所以，，
因为双曲线的渐近线：，所以其倾斜角分别为和，
又因为直线与双曲线的右支交于，两点，
所以直线的倾斜角范围为，易得
所以，
由，不妨令，，
易知，在上单调递减，在上单调递增，
故的最小值为，又因为，
从而在上的值域为，
所以的取值范围为，
又因为，
所以的取值范围为.
故答案为：.
5．（2020·山东青岛·高三开学考试）已知直线：与抛物线：在第一象限的交点为，过的焦点，，则抛物线的准线方程为_______；_______.
【答案】
【解析】
易知直线与轴的交点为，即抛物线的焦点为，∴准线方程为，
设，则，，作轴于点，如图，
则，，∴，
∴直线的斜率为．
故答案为：；．
6．（2020·江苏如皋·高二月考）已知是抛物线的焦点，，为抛物线上任意一点，的最小值为，则________；若过的直线交抛物线于、两点，有，则________.
【答案】
【解析】
过点作垂直于抛物线的准线，垂足为点，
由抛物线的定义可得，
，则，则点在抛物线内，如下图所示：
，当点、、共线时，取得最小值，解得，
所以，抛物线的标准方程为，该抛物线的焦点为，
设点、，可知直线不与轴重合，设直线的方程为，
联立，可得，恒成立，
由韦达定理得，，
，则，，
所以，，可得，
，可得，
因此，.
故答案为：；.
7．（2021·天津南开区·南开中学高三月考）设椭圆：的左焦点为，离心率为，过点且与轴垂直的直线被椭圆截得的线段长为．
（1）求椭圆的方程；
（2）设，分别为椭圆的左、右顶点，过点且斜率为的直线与椭圆交于点，两点，且，求的值．
【答案】（1）；（2）.
【分析】
(1)利用椭圆的离心率，和过点F且与x轴垂直的直线被椭圆截得的线段长为，列出方程求解，可得椭圆的方程；
(2)联立直线CD和椭圆方程，利用韦达定理和向量数量积的坐标公式代入解出k的值．
【详解】
（1）设F(－c，0)，由，知．过点F且与x轴垂直的直线为x＝－c，代入椭圆方程有，
解得，于是，解得，又，从而，c＝1，
所以椭圆的方程为．
（2）设点C(x1，y1)，D(x2，y2)，由F(－1，0)得直线CD的方程为y＝k(x＋1)，
由方程组消去y，整理得(2＋3k2)x2＋6k2x＋3k2－6＝0．
求解可得x1＋x2＝，x1x2＝．因为A(，0)，B(，0)，
所以·＋·＝(x1＋，y1)·(－x2，－y2)＋(x2＋，y2)·(－x1，－y1)
＝6－2x1x2－2y1y2＝6－2x1x2－2k2(x1＋1)(x2＋1)＝6－(2＋2k2)x1x2－2k2(x1＋x2)－2k2＝．
由已知得，解得k＝．
8．（2021·北京）在平面直角坐标系xOy中，抛物线C的焦点在y轴上，且抛物线上的点P(x0,4)到焦点F的距离为5.斜率为2的直线l与抛物线C交于A，B两点.
（1）求抛物线C的标准方程，及抛物线在P点处的切线方程；
（2）若AB的垂直平分线分别交y轴和抛物线于M，N两点（M，N位于直线l两侧），当四边形AMBN为菱形时，求直线l的方程.
【答案】（1）；切线方程为或；（2）.
【分析】
（1）利用抛物线定义，结合已知即可求参数，写出抛物线标准方程，即可得P点坐标，利用导数的几何意义求P点处切线的斜率，即可写出切线方程.
（2）设直线为，，，联立抛物线并整理，应用韦达定理求，，再根据中点公式求的中点，并写出的垂直平分线方程，利用菱形的对称性求N点坐标，由点在直线上求参数m，即可得直线l的方程.
【详解】
（1）依题意,设抛物线C：， 由P到焦点F的距离为5，
∴P到准线的距离为5，又P(x0,4)，
∴由抛物线准线方程得：，即，则抛物线的标准方程为.
∴，则，点P(±4,4)，
∴，.
∴(4,4)处抛物线切线方程为，即；
(4,4)处抛物线切线方程为，即.
综上，点处抛物线切线方程为或.
（2）设直线的方程为，，，
联立抛物线得： ，消y得 ，.
∴，，则，，即的中点为.
∴的垂直平分线方程为.
∵四边形AMBN为菱形，
∴，，关于对称，则，又在抛物线上，
∴，即，
故直线的方程为 .
9. （2019·天津高考真题（文）） 设椭圆的左焦点为，左顶点为，上顶点为B.已知（为原点）.
（Ⅰ）求椭圆的离心率；
（Ⅱ）设经过点且斜率为的直线与椭圆在轴上方的交点为，圆同时与轴和直线相切，圆心在直线上，且，求椭圆的方程.
【答案】（I）；（II）.
【解析】
（I）解：设椭圆的半焦距为，由已知有，
又由，消去得，解得，
所以，椭圆的离心率为.
（II）解：由（I）知，，故椭圆方程为，
由题意，，则直线的方程为，
点的坐标满足，消去并化简，得到，
解得，
代入到的方程，解得，
因为点在轴的上方，所以，
由圆心在直线上，可设，因为，
且由（I）知，故，解得，
因为圆与轴相切，所以圆的半径为2，
又由圆与相切，得，解得，
所以椭圆的方程为：.
10．（2019·全国高三月考（理））如图，己知抛物线，直线交抛物线于两点，是抛物线外一点，连接分别交地物线于点，且.
（1）若，求点的轨迹方程.
（2）若，且平行x轴，求面积.
【答案】（1）（2）
【解析】
（1）解法1：，设，
则，由可得
，故，同理，
故，代入抛物线得：，
化简得：，
同理得：，
所以为方程的两根，
又由，
将代入且①，
将代入①，得，故.
故点P的轨迹方程为.
解法2：同解法1知
，
设线段的中点分别为，易知三点共线，
（为实数），所以.
以下同解法1.
（2）由为方程的两根，
可得：.
由（1）得，因为，所以，故.
轴且在抛物线上，∴关于轴对称.
，及，
且.
∵在抛物线上,，解得.
设的中点为，则，
所以，
而.
练真题TIDHNEG
1. （2021·天津高考真题）已知双曲线的右焦点与抛物线的焦点重合，抛物线的准线交双曲线于A，B两点，交双曲线的渐近线于C、D两点，若．则双曲线的离心率为（ ）
A．B．C．2D．3
【答案】A
【分析】
设公共焦点为，进而可得准线为，代入双曲线及渐近线方程，结合线段长度比值可得，再由双曲线离心率公式即可得解.
【详解】
设双曲线与抛物线的公共焦点为，
则抛物线的准线为，
令，则，解得，所以,
又因为双曲线的渐近线方程为，所以，
所以，即，所以，
所以双曲线的离心率.
故选：A.
2.（2020·全国高考真题（理））已知F为双曲线的右焦点，A为C的右顶点，B为C上的点，且BF垂直于x轴.若AB的斜率为3，则C的离心率为______________.
【答案】2
【解析】
联立，解得，所以.
依题可得，，，即，变形得，,
因此，双曲线的离心率为.
故答案为：．
3.（2019·浙江高考真题）已知椭圆的左焦点为，点在椭圆上且在轴的上方，若线段的中点在以原点为圆心，为半径的圆上，则直线的斜率是_______.
【答案】
【解析】
方法1：由题意可知，
由中位线定理可得，设可得，
联立方程
可解得（舍），点在椭圆上且在轴的上方，
求得，所以
方法2：焦半径公式应用
解析1：由题意可知，
由中位线定理可得，即
求得，所以.
4.（2020·全国高考真题（文））已知椭圆的离心率为，，分别为的左、右顶点．
（1）求的方程；
（2）若点在上，点在直线上，且，，求的面积．
【答案】（1）；（2）.
【解析】
（1）
，，
根据离心率，
解得或(舍)，
的方程为：，
即；
（2）不妨设,在x轴上方
点在上，点在直线上，且，，
过点作轴垂线，交点为，设与轴交点为
根据题意画出图形，如图
，，，
又，，
，
根据三角形全等条件“”，
可得：，
，
，
，
设点为，
可得点纵坐标为，将其代入，
可得：，
解得：或，
点为或，
①当点为时，
故，
，
，
可得：点为，
画出图象，如图
,，
可求得直线的直线方程为：，
根据点到直线距离公式可得到直线的距离为：，
根据两点间距离公式可得：，
面积为：；
②当点为时，
故，
，
，
可得：点为，
画出图象，如图
,，
可求得直线的直线方程为：，
根据点到直线距离公式可得到直线的距离为：，
根据两点间距离公式可得：，
面积为：，
综上所述，面积为：.
5．（2019·江苏高考真题）如图，在平面直角坐标系xOy中，椭圆C:的焦点为F1（–1、0），F2（1，0）．过F2作x轴的垂线l，在x轴的上方，l与圆F2:交于点A，与椭圆C交于点D.连结AF1并延长交圆F2于点B，连结BF2交椭圆C于点E，连结DF1．已知DF1=．
（1）求椭圆C的标准方程；
（2）求点E的坐标．
【答案】（1）；
（2）.
【解析】
（1）设椭圆C的焦距为2c.
因为F1(－1，0)，F2(1，0)，所以F1F2=2，c=1.
又因为DF1=，AF2⊥x轴，所以DF2=，
因此2a=DF1+DF2=4，从而a=2.
由b2=a2-c2，得b2=3.
因此，椭圆C的标准方程为.
（2）解法一：
由（1）知，椭圆C：，a=2，
因为AF2⊥x轴，所以点A的横坐标为1.
将x=1代入圆F2的方程(x-1) 2+y2=16，解得y=±4.
因为点A在x轴上方，所以A(1，4).
又F1(-1，0)，所以直线AF1：y=2x+2.
由，得，
解得或.
将代入，得，
因此.又F2(1，0)，所以直线BF2：.
由，得，解得或.
又因为E是线段BF2与椭圆的交点，所以.
将代入，得.因此.
解法二：
由（1）知，椭圆C：.如图，连结EF1.
因为BF2=2a，EF1+EF2=2a，所以EF1=EB，
从而∠BF1E=∠B.
因为F2A=F2B，所以∠A=∠B，
所以∠A=∠BF1E，从而EF1∥F2A.
因为AF2⊥x轴，所以EF1⊥x轴.
因为F1(-1，0)，由，得.
又因为E是线段BF2与椭圆的交点，所以.
因此.
6．（2021·山东高考真题）已知抛物线的顶点是坐标原点，焦点在轴的正半轴上，是抛物线上的点，点到焦点的距离为1，且到轴的距离是．
（1）求抛物线的标准方程；
（2）假设直线通过点，与抛物线相交于，两点，且，求直线的方程．
【答案】（1）；（2）．
【分析】
（1）根据抛物线的定义，结合到焦点、轴的距离求，写出抛物线方程.
（2）直线的斜率不存在易得与不垂直与题设矛盾，设直线方程联立抛物线方程，应用韦达定理求，，进而求，由题设向量垂直的坐标表示有求直线方程即可.
【详解】
（1）由己知，可设抛物线的方程为，又到焦点的距离是1，
∴点到准线的距离是1，又到轴的距离是，
∴，解得，则抛物线方程是．
（2）假设直线的斜率不存在，则直线的方程为，与联立可得交点、的坐标分别为，，易得，可知直线与直线不垂直，不满足题意，故假设不成立，
∴直线的斜率存在．设直线为，整理得，
设，，联立直线与抛物线的方程得，
消去，并整理得，于是，，
∴，
又，因此，即，
∴，解得或．
当时，直线的方程是，不满足，舍去．
当时，直线的方程是，即，
∴直线的方程是．