高考数学核心考点专题训练专题8函数的图象及应用(原卷版+解析)

这是一份高考数学核心考点专题训练专题8函数的图象及应用(原卷版+解析)，共17页。试卷主要包含了单选题，单空题，解答题等内容，欢迎下载使用。

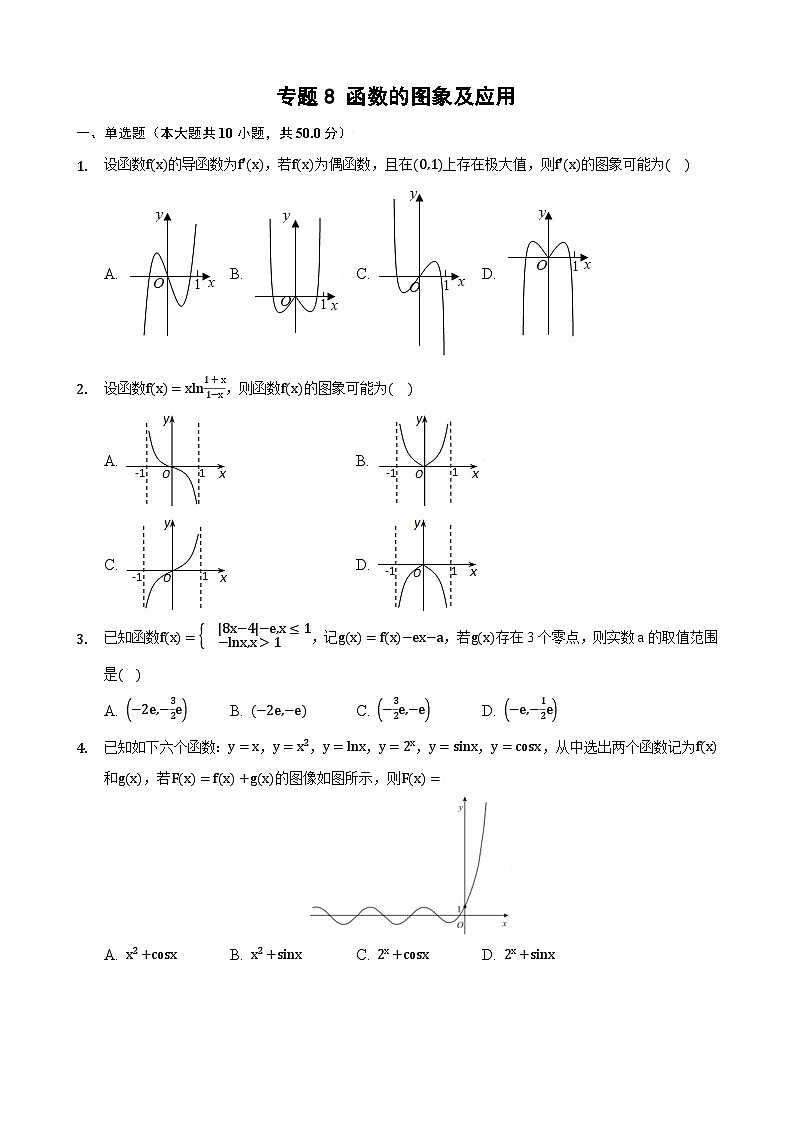
设函数f(x)的导函数为f'(x)，若f(x)为偶函数，且在(0,1)上存在极大值，则f'(x)的图象可能为( )
A. B. C. D.
设函数f(x)=xln1+x1−x，则函数f(x)的图象可能为( )
A. B.
C. D.
已知函数fx=8x−4−e,x≤1−lnx,x>1，记gx=fx−ex−a，若gx存在3个零点，则实数a的取值范围是( )
A. −2e,−32eB. −2e,−eC. −32e,−eD. −e,−12e
已知如下六个函数：y=x，y=x2，y=lnx，y=2x，y=sinx，y=csx，从中选出两个函数记为fx和gx，若Fx=fx+gx的图像如图所示，则Fx=
A. x2+csxB. x2+sinxC. 2x+csxD. 2x+sinx
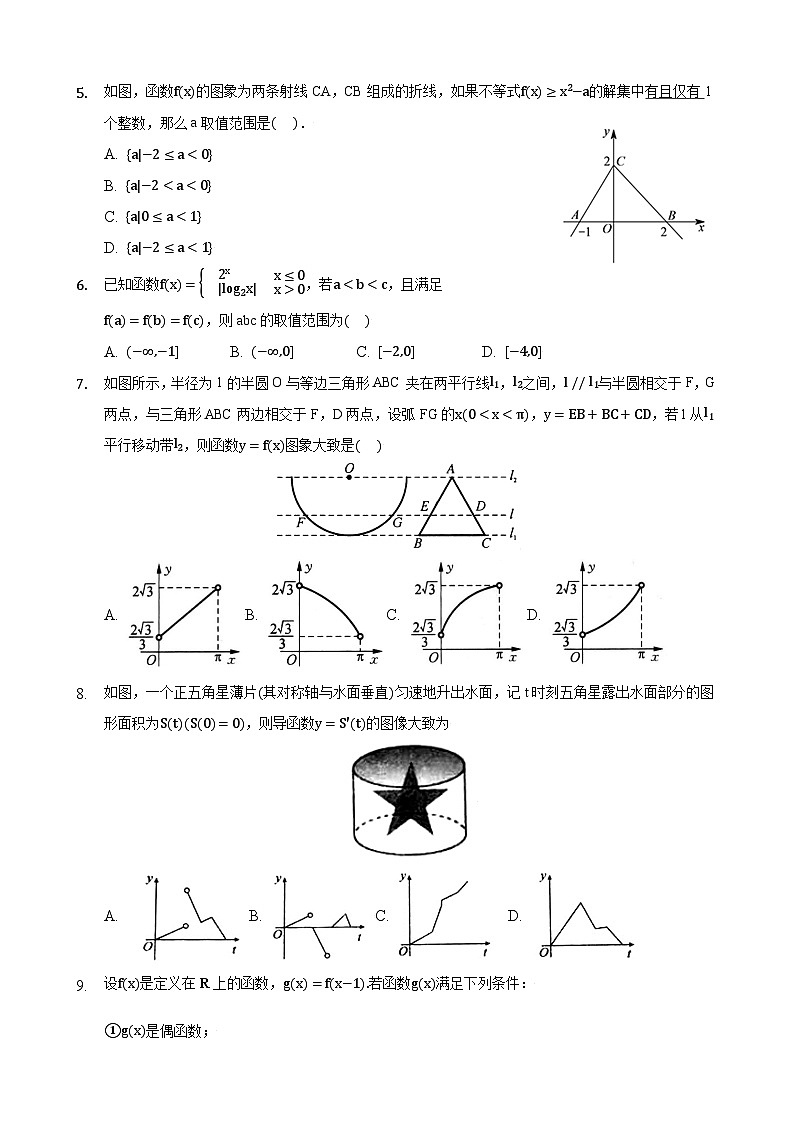
如图，函数fx的图象为两条射线CA，CB组成的折线，如果不等式fx≥x2−a的解集中有且仅有1个整数，那么a取值范围是( )．
A. a|−2≤a<0
B. a|−2C. a|0≤a<1
D. a|−2≤a<1
已知函数f(x)=2x|lg2x| x≤0x>0，若aA. (−∞,−1]B. (−∞,0]C. [−2,0]D. [−4,0]
如图所示，半径为1的半圆O与等边三角形ABC夹在两平行线l1，l2之间，l // l1与半圆相交于F，G两点，与三角形ABC两边相交于F，D两点，设弧FG的x(0A. B. C. D.
如图，一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面，记t时刻五角星露出水面部分的图形面积为S(t)(S(0)=0)，则导函数y=S'(t)的图像大致为
A. B. C. D.
设f(x)是定义在R上的函数，g(x)=f(x−1).若函数g(x)满足下列条件：
①g(x)是偶函数；
②g(x)在区间[0,+∞)上是增函数；
③g(x)有一个零点为2．
则不等式(x+1)f(x)>0的解集是
A. (−3,−1)∪(1,+∞)B. (1,+∞)
C. (−∞,−3)∪(1,+∞)D. (−∞,−1)∪(1,+∞)
已知函数f(x)是定义在R上的奇函数，当x>0时，f(x)=4−x−1，g(x)=x2+2x,x<0lg2(x+1),x≥0，若g(f(a))≤3，则实数a的取值范围为( )
A. −12,12B. −3,−2∪0,12
C. −12,−2∪0,8D. −2,8
二、单空题（本大题共4小题，共20.0分）
若函数y=f(x)图象上不同两点M，N关于原点对称，则称点对[M,N]是函数y=f(x)的一对“和谐点对”(点对[M,N]与[N,M]看作同一对“和谐点对”).已知函数f(x)=ex,x<0,x2−4x,x>0,则此函数的“和谐点对”有_______对．
已知函数f(x)=|x−1|+|x+1|−12|x|，若函数g(x)=f(x)−b恰有四个零点，则实数b的取值范围是________．
已知函数f(x)=|lg2|1−x||(a>0，且a≠1)，若x1函数y=f(x)是定义域为R的偶函数，当x≥0时，f(x)=x216,(0≤x≤2)52x−1,(x>2)，若关于x的方程[f(x)]2+af(x)+b=0，a,b∈R，有且仅有6个不同实数根，则实数a的取值范围是_____________．
三、解答题（本大题共3小题，共30分）
已知函数fx=sinωx+φ+bω>0,0<φ<π的图象两相邻对称轴之间的距离是π2，若将fx的图象先向右平移π3个单位长度，再向上平移2个单位长度后，所得图象关于y轴对称且经过坐标原点．
(1)求fx的解析式；
(2)若对任意x∈0,π4，fx2−afx+a+1≤0恒成立，求实数a的取值范围．
已知二次函数f(x)满足f(x+1)−f(x)=2x，且f(0)=1．
(1)求f(x)的解析式;
(2)在区间[−1,1]上，函数y=f(x)的图象恒在直线y=2x+m的图象上方，试确定实数m的取值范围．






已知①函数f(x)=3sinωxcsωx+cs2ωx(ω>0)，周期是π2；②函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ|<π2,k∈R)的图像如图所示；在以上两个条件中选择一个解答下列问题．(注：如果选择多个条件分别进行解答，则按第一个解答进行计分．)
(1)求f(x)的解析式，以及x∈−π12,7π24时f(x)的值域；
(2)将f(x)图像上所有点的横坐标扩大到原来的2倍，纵坐标不变，再向左平移π3个单位，最后将整个函数图像向上平移32个单位后得到函数g(x)的图像，若|g(x)−m|<1成立的充分条件是0≤x≤5π12，求m的取值范围．
专题8 函数的图象及应用
一、单选题（本大题共10小题，共50.0分）
设函数f(x)的导函数为f'(x)，若f(x)为偶函数，且在(0,1)上存在极大值，则f'(x)的图象可能为( )
A. B. C. D.
【答案】C
【解析】解：根据题意，若f(x)为偶函数，则其导数f'(x)为奇函数，
分析选项：可以排除B、D，
又由函数f(x)在(0,1)上存在极大值，则其导数图象在(0,1)上存在零点，且零点左侧导数值符号为正，右侧导数值符号为负，
分析选项：可以排除A，C符合；
故选：C．
设函数f(x)=xln1+x1−x，则函数f(x)的图象可能为( )
A. B.
C. D.
【答案】B
【解析】解：函数f(x)=xln1+x1−x的定义域为(−1,1)，
由f(−x)=−xln1−x1+x=xln1+x1−x=f(x)，得f(x)为偶函数，排除A，C；
又f(12)=12ln1+121−12=12ln3>0，排除D．
故选：B．
已知函数fx=8x−4−e,x≤1−lnx,x>1，记gx=fx−ex−a，若gx存在3个零点，则实数a的取值范围是( )
A. −2e,−32eB. −2e,−eC. −32e,−eD. −e,−12e
【答案】C
【解析】解：结合函数f(x)={|8x−4|−e,x⩽1−1nx,x>1 与y=ex+a的图像，
若gx=fx−ex−a存在三个零点，则y=ex+a在点12,−e上方，在1,0下方
∴−e<12e+ae+a<0解得：−32e故选C．
已知如下六个函数：y=x，y=x2，y=lnx，y=2x，y=sinx，y=csx，从中选出两个函数记为fx和gx，若Fx=fx+gx的图像如图所示，则Fx=
A. x2+csxB. x2+sinxC. 2x+csxD. 2x+sinx
【答案】D
【解析】解：由图象可知，函数F(x)过定点(0,1)，
当x>0时，F(x)>1，为增函数，当x<0时，F(x)>0或，F(x)<0交替出现，
因为y=2x的图象经过点(0,1)，且当x>0时，y>1，当x<0时，0若为y=csx，当x=0时，y=1，2x+csx不满足过点(0,1)，
所以只有当F(x)=2x+sinx才满足条件，
故选：D．
如图，函数fx的图象为两条射线CA，CB组成的折线，如果不等式fx≥x2−a的解集中有且仅有1个整数，那么a取值范围是( )．
A. a|−2≤a<0
B. a|−2C. a|0≤a<1
D. a|−2≤a<1
【答案】A
【解析】解：fx=２ｘ+２,ｘ⩽０−ｘ+２,ｘ>０，不等式fx≥x2−a等价于a⩾x2−fx，
设g(x)=x2−f(x)=x2−2x−2 ,x≤0x2+x−2 ,x>0，
x≤0，g'(x)=2x−2<0，函数单调递减，
x>0，g'(x)=2x+1>0，函数单调递增，
又g(0)=−2，g(1)=1+1−2=0，g(−1)=1+2−2=1，
要使a≥g(x)只有1个整数，那么a取值范围是−2⩽a<0．
故选A．
已知函数f(x)=2x|lg2x| x≤0x>0，若aA. (−∞,−1]B. (−∞,0]C. [−2,0]D. [−4,0]
【答案】B
【解析】解：由函数fx=2x,x≤0lg2x,x>0，作出函数的图象；
结合函数fx=2x,x≤0lg2x,x>0图象可得a∈−∞,0,12≤b<1由f(a)=f(b)=f(c)可得−lg2b=lg2c，从而bc=1．
所以abc=a∈−∞,0．
故选B．
如图所示，半径为1的半圆O与等边三角形ABC夹在两平行线l1，l2之间，l // l1与半圆相交于F，G两点，与三角形ABC两边相交于F，D两点，设弧FG的x(0A. B. C. D.
【答案】D
【解析】解：当x=0时，y=EB+BC+CD=BC=233；
当x=π时，此时y=AB+BC+CA=3×233=23；
当x=π3时，∠FOG=π3，三角形OFG为正三角形，此时AM=OH=32，在正△AED中，AE=ED=DA=1，
∴y=EB+BC+CD=AB+BC+CA−(AE+AD)=3×233−2×1=23−2.如图，
又当x=π3时，图中y0=233+13(23−233)=1039>23−2．
故当x=π3时，对应的点(x,y)在图中红色连线段的下方，对照选项，D正确．
故选D.
如图，一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面，记t时刻五角星露出水面部分的图形面积为S(t)(S(0)=0)，则导函数y=S'(t)的图像大致为
A. B. C. D.
【答案】A
【解析】【试题解析】
解：最初零时刻和最后终点时刻没有变化，导数取零，排除C；
总面积一直保持增加，没有负的改变量，排除B；
考察A、D的差异在于两肩位置的改变是否平滑，考虑到导数的意义，判断此时面积改变为突变，产生中断，选择A．
故选：A
设f(x)是定义在R上的函数，g(x)=f(x−1).若函数g(x)满足下列条件：
①g(x)是偶函数；
②g(x)在区间[0,+∞)上是增函数；
③g(x)有一个零点为2．
则不等式(x+1)f(x)>0的解集是
A. (−3,−1)∪(1,+∞)B. (1,+∞)
C. (−∞,−3)∪(1,+∞)D. (−∞,−1)∪(1,+∞)
【答案】A
【解析】解：由g(x)=f(x−1)，可得g(x+1)=f(x)，即f(x)为g(x)向左平移一个单位得到．
故由g(x)是偶函数，可得f(x)关于直线x=−1对称；
又由g(x)在区间[0,+∞)上是增函数，可得f(x)在区间[−1,+∞)上是增函数；
由g(x)有一个零点为2，可得f(x)有一个零点为1，
结合图象，
可得f(x)>0的解集为−∞,−3∪1,+∞，f(x)<0的解集为−3,1，
(x+1)f(x)>0即x+1>0fx>0或x+1<0fx<0,
解得x>1或−3故不等式解集为(−3,−1)∪(1,+∞)．
故选A．
已知函数f(x)是定义在R上的奇函数，当x>0时，f(x)=4−x−1，g(x)=x2+2x,x<0lg2(x+1),x≥0，若g(f(a))≤3，则实数a的取值范围为( )
A. −12,12B. −3,−2∪0,12
C. −12,−2∪0,8D. −2,8
【答案】C
【解析】由g(x)≤3可得，
当x<0时，x2+2x⩽3，得−3⩽x<0，
当x⩾0时，lg2(x+1)⩽3，得0⩽x⩽7，
故g(x)≤3的解为{x|−3⩽x⩽7}
∴g(f(a))≤3的解即−3≤f(a)≤7的解，
函数f(x)=4−x−1,x>00, x=0−4+x+1,x<0
作出f(x)的图象如下，
∵f(12)=−7，f(8)=−3，∴f(−12)=7，
∴当a∈[−12,−2]∪[0,8]时，g(f(a))≤3.
故选C．
二、单空题（本大题共4小题，共20.0分）
若函数y=f(x)图象上不同两点M，N关于原点对称，则称点对[M,N]是函数y=f(x)的一对“和谐点对”(点对[M,N]与[N,M]看作同一对“和谐点对”).已知函数f(x)=ex,x<0,x2−4x,x>0,则此函数的“和谐点对”有_______对．
【答案】2
【解析】 作出函数f(x)={ex,x<0,x2−4x,x>0的图象，f(x)的“和谐点对”数可转化为y1=ex(x<0)和y2=−x2−4x(x<0)的图象的交点个数(如图)．
由图象知，函数f(x)有两对“和谐点对”．
已知函数f(x)=|x−1|+|x+1|−12|x|，若函数g(x)=f(x)−b恰有四个零点，则实数b的取值范围是________．
【答案】32,2
【解析】由题意，分段函数fx的解析式为
fx=32x, x⩾12−12x, 0⩽x<12+12x, −1⩽x<0−32x, x<−1，其图像如下图所示：
由图像可知，当b∈32,2时，方程fx=b有4个交点，
此时函数gx=fx−b=0恰有四个零点．
故答案为32,2．
已知函数f(x)=|lg2|1−x||(a>0，且a≠1)，若x1【答案】2
【解析】因为f(x)=|lga|x−1||a>0且a≠1，
所以f(x)的图象关于x=1对称，
又因为x1所以x1故lga|x1−1|=−lga|x2−1|,−lga|x3−1|=lga|x4−1|，
即(x1−1)(x2−1)=1,(x3−1)(x4−1)=1，
解得x1x2=x1+x2,x3x4=x3+x4，
所以1x1+1x2+1x3+1x4=x1+x2x1x2+x3+x4x3x4=1+1=2．
故答案为2．
函数y=f(x)是定义域为R的偶函数，当x≥0时，f(x)=x216,(0≤x≤2)52x−1,(x>2)，若关于x的方程[f(x)]2+af(x)+b=0，a,b∈R，有且仅有6个不同实数根，则实数a的取值范围是_____________．
【答案】(−14,1)∪(−12,−14)
【解析】作出f(x)的函数图象如图所示：

令f(x)=t，显然，当t=0时，方程f(x)=t有三个解，
当0当t=14或−1当t≤−1或t>14时，方程f(x)=t无解．
∵关于x的方程[f(x)]2+af(x)+b=0，a，b∈R有且仅有6个不同实数根，
∴关于t的方程t2+at+b=0，t∈R有两根，
不妨设为t1,t2，且t1=14,0∴t1+t2∈(14,12)或者t1+t2∈(−1,14)；
又∵−a=t1+t2，
∴a∈(−14,1)∪(−12,−14)，
故答案为：(−14,1)∪(−12,−14)
三、解答题（本大题共3小题，共30分）
已知函数fx=sinωx+φ+bω>0,0<φ<π的图象两相邻对称轴之间的距离是π2，若将fx的图象先向右平移π3个单位长度，再向上平移2个单位长度后，所得图象关于y轴对称且经过坐标原点．
(1)求fx的解析式；
(2)若对任意x∈0,π4，fx2−afx+a+1≤0恒成立，求实数a的取值范围．
【答案】解：(1)由题意f(x)=sin (ωx+φ)+b(ω>0,0<φ<π)，其周期为T=π2×2=π，
故T=2πω=π，即得ω=2.
将f(x)的图象向右平移π3个单位长度，再向上平移2个单位长度得到y=sin (2(x−π3)+φ)+b+2．
即y=sin (2x+φ−2π3)+b+2，由题设条件得φ−2π3=π2+kπ，即φ=7π6+kπ, k∈Z，
因为0<φ<π，当k=−1时满足条件，即φ=π6，
又函数fx的图像经过坐标原点，即得
sin (φ−2π3)+b+2=0，故b=−1.
故f(x)=sin (2x+π6)−1．
(2)因为x∈[0,π4]，故2x+π6∈[π6,2π3]，
故sin (2x+π6)∈[12,1]，f(x)∈[−12,0]．
设t=f(x)∈[−12,0]，即t2−at+a+1⩽0恒成立．
即g(t)=t2−at+a+1的最大值小于等于零即可．
故满足：g(−12)⩽0g(0)⩽0,
即14+12a+a+1⩽0a+1⩽0 ，解得a⩽−1．
故实数a的取值范围为−∞,−1．已知二次函数f(x)满足f(x+1)−f(x)=2x，且f(0)=1．
(1)求f(x)的解析式;
(2)在区间[−1,1]上，函数y=f(x)的图象恒在直线y=2x+m的图象上方，试确定实数m的取值范围．
【答案】解：(1)由f(0)=1，可设f(x)=ax2+bx+1(a≠0)，
故f(x+1)−f(x)=a(x+1)2+b(x+1)+1−(ax2+bx+1)=2ax+a+b，
又f(x+1)−f(x)=2x，所以2a=2a+b=0，
解得a=1b=−1，故f(x)=x2−x+1．
(2)由题意，得x2−x+1>2x+m，即x2−3x+1>m，对x∈[−1,1]恒成立．
令g(x)=x2−3x+1(x∈[−1,1])，则问题可转化为g(x)min>m．
又g(x)在[−1,1]上单调递减，所以g(x)min=g(1)=−1，故m<−1．
所以m的取值范围为(−∞,−1)．
已知①函数f(x)=3sinωxcsωx+cs2ωx(ω>0)，周期是π2；②函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ|<π2,k∈R)的图像如图所示；在以上两个条件中选择一个解答下列问题．(注：如果选择多个条件分别进行解答，则按第一个解答进行计分．)
(1)求f(x)的解析式，以及x∈−π12,7π24时f(x)的值域；
(2)将f(x)图像上所有点的横坐标扩大到原来的2倍，纵坐标不变，再向左平移π3个单位，最后将整个函数图像向上平移32个单位后得到函数g(x)的图像，若|g(x)−m|<1成立的充分条件是0≤x≤5π12，求m的取值范围．
【答案】解：选择条件 ①解答如下
(1)f(x)=3sinωxcsωx+cs2ωx
=32sin2ωx+12(cs2ωx+1)
=sin(2ωx+π6)+12
由T=2π2ω=π2，解得ω=2，
所以函数f(x)=sin(4x+π6)+12
因为x∈[−π12,7π24]，
所以−π6≤4x+π6≤4π3，
所以1−32≤sin(4x+π6)+12≤32，
即函数f(x)在x∈[−π12,7π24]上的值域是1−32,32
(2)将f(x)图象上所有点的横坐标扩大到原来的2倍，得y=sin(2x+π6)+12，
纵坐标不变，再向左平移π3个单位，
得y=sin[2(x+π3)+π6]+12=sin(2x+5π6)+12，
最后将整个函数图象向上平移32个单位后，
得到g(x)=sin(2x+5π6)+12+32=sin(2x+5π6)+2
因为|g(x)−m|<1，
所以g(x)−1∵|g(x)−m|<1成立的充分条件是0≤x≤5π12，
∴当x∈[0,5π12]时，g(x)−1所以只需[g(x)−1]max当x∈[0,5π12]时，2x+5π6∈[5π6,5π3]，
所以g(x)max=g(0)=12+2=52，g(x)min=g(π3)=−1+2=1，
从而[g(x)−1]max=32，[g(x)+1]min=2，即32所以m的取值范围是(32,2)
选择条件 ②解答如下：
(1)由己知A=32−(−12)2=1，k=32+(−12)2=12，
∵T2=π3−π12=π4，
∴T=π2，∴ω=2πT=4，
∴f(x)=sin(4x+φ)+12，过点(π12,32)，且|φ|<π2，
∴4×π12+φ=π2，∴φ=π6，
∴f(x)=sin(4x+π6)+12
因为x∈[−π12,7π24]，
所以−π6≤4x+π6≤4π3，
所以1−32≤sin(4x+π6)+12≤32，
即函数f(x)在x∈[−π12,7π24]上的值域是1−32,32
(2)将f(x)图象上所有点的横坐标扩大到原来的2倍，得y=sin(2x+π6)+12，
纵坐标不变，再向左平移π3个单位，
得y=sin[2(x+π3)+π6]+12=sin(2x+5π6)+12，
最后将整个函数图象向上平移32个单位后，
得到g(x)=sin(2x+5π6)+12+32=sin(2x+5π6)+2，
因为|g(x)−m|<1，
所以g(x)−1∵|g(x)−m|<1成立的充分条件是0≤x≤5π12，
∴当x∈[0,5π12]时，g(x)−1所以只需[g(x)−1]max当x∈[0,5π12]时，2x+5π6∈[5π6,5π3]，
所以g(x)max=g(0)=12+2=52，g(x)min=g(π3)=−1+2=1，
从而[g(x)−1]max=32，[g(x)+1]min=2，即32所以m的取值范围是(32,2)