高考数学核心考点专题训练专题28空间几何体的直观图与三视图(原卷版+解析)

这是一份高考数学核心考点专题训练专题28空间几何体的直观图与三视图(原卷版+解析)，共18页。试卷主要包含了单选题，单空题，解答题等内容，欢迎下载使用。
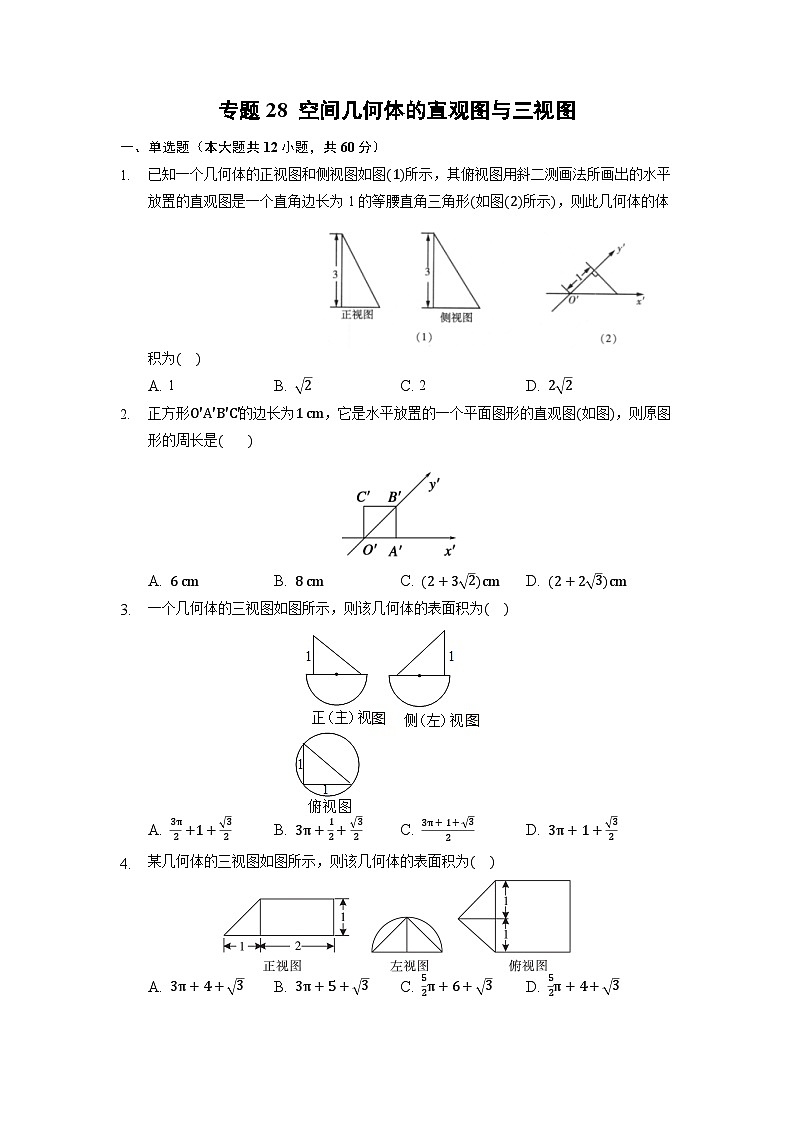
已知一个几何体的正视图和侧视图如图(1)所示，其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图(2)所示)，则此几何体的体积为( )
A. 1B. 2C. 2D. 22
正方形O'A'B'C'的边长为1 cm，它是水平放置的一个平面图形的直观图(如图)，则原图形的周长是( )
A. 6 cmB. 8 cmC. (2+32)cmD. (2+23)cm
一个几何体的三视图如图所示，则该几何体的表面积为( )
A. 3π2+1+32B. 3π+12+32C. 3π+1+32D. 3π+1+32
某几何体的三视图如图所示，则该几何体的表面积为( )
A. 3π+4+3B. 3π+5+3C. 52π+6+3D. 52π+4+3
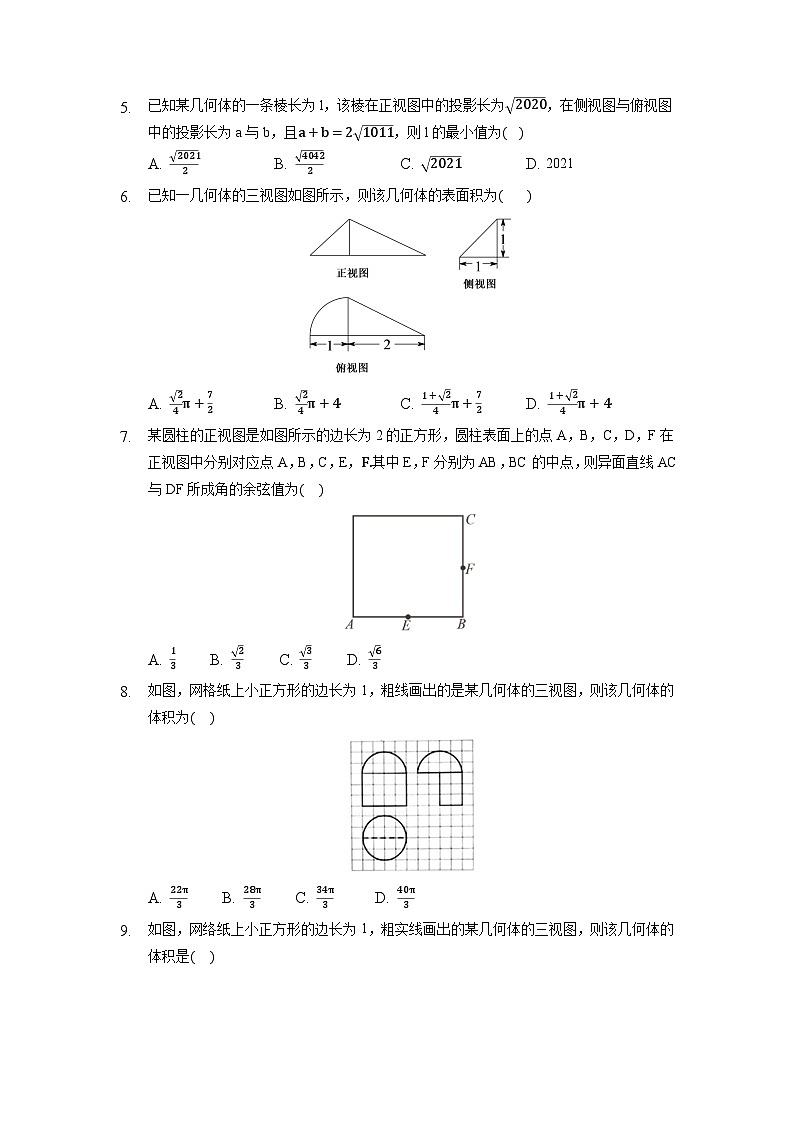
已知某几何体的一条棱长为l，该棱在正视图中的投影长为2020，在侧视图与俯视图中的投影长为a与b，且a+b=21011，则l的最小值为( )
A. 20212B. 40422C. 2021D. 2021
已知一几何体的三视图如图所示，则该几何体的表面积为( )
A. 24π+72B. 24π+4C. 1+24π+72D. 1+24π+4
某圆柱的正视图是如图所示的边长为2的正方形，圆柱表面上的点A，B，C，D，F在正视图中分别对应点A，B，C，E，F.其中E，F分别为AB，BC的中点，则异面直线AC与DF所成角的余弦值为( )
A. 13 B. 23 C. 33 D. 63
如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为( )
A. 22π3 B. 28π3 C. 34π3 D. 40π3
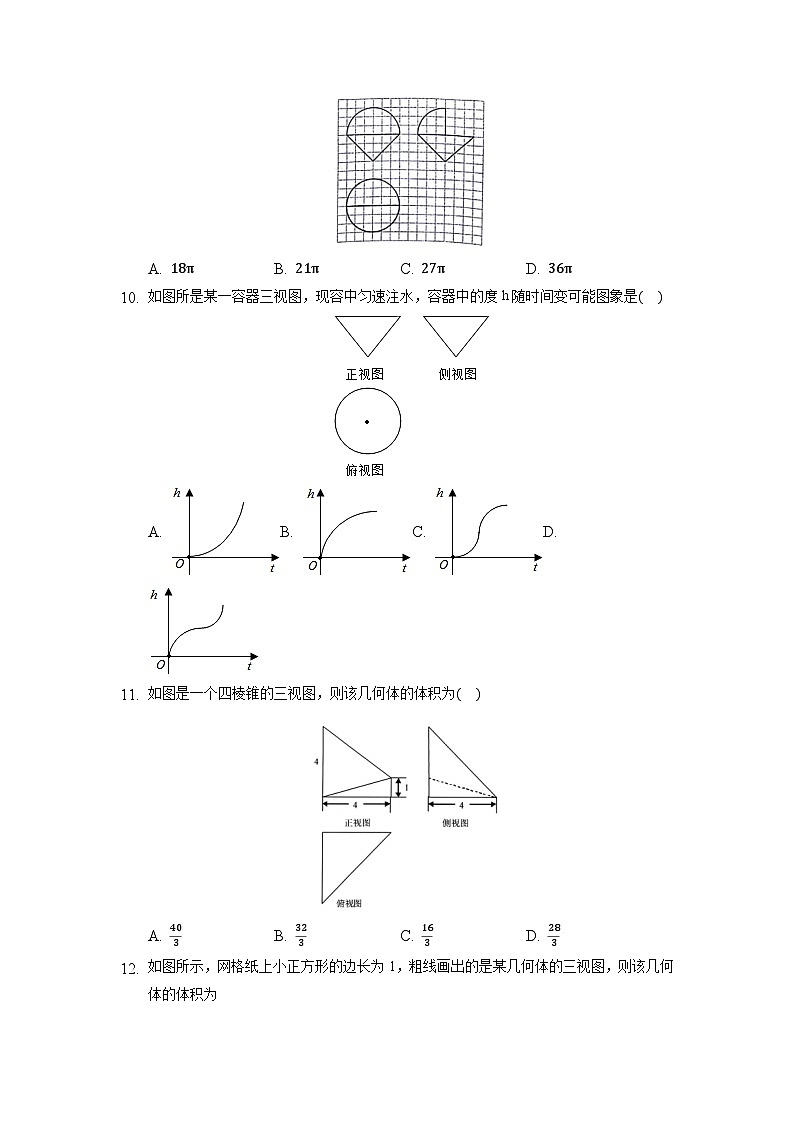
如图，网络纸上小正方形的边长为1，粗实线画出的某几何体的三视图，则该几何体的体积是( )
A. 18πB. 21πC. 27πD. 36π
如图所是某一容器三视图，现容中匀速注水，容器中的度h随时间变可能图象是( )
A. B. C. D.
如图是一个四棱锥的三视图，则该几何体的体积为( )
A. 403B. 323C. 163D. 283
如图所示，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为
A. 64−82π3 B. 64−42π3 C. 64−8π3 D. 64−4π3
二、单空题（本大题共4小题，共20分）
某组合体的正视图和侧视图如图(1)所示，它的俯视图的直观图是图(2)中粗线所表示的平面图形，其中四边形O'A'B'C'为平行四边形，D'为C'B'的中点，则图(2)中平行四边形O'A'B'C'的面积为___________．
以图①为正视图，在图②③④⑤中选两个分别作为侧视图和附视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为_____________(写出符合求的一组答案即可)．
在棱长为1的正方体ABCD−A1B1C1D1中，点M，N分别是棱B1C1，C1D1的中点，过A，M，N三点作正方体的截面，将截面多边形向平面ADD1A1作投影，则投影图形的面积为 ．
把平面图形α上的所有点在另一个平面上的射影所构成的图形β称为图形α在这个平面上的射影，如图所示，在三棱锥A−BCD中，BC⊥DC，AD⊥DC，BC⊥AB，BC=CD=4，AC=43，则△ADB在平面ABC上的射影的面积是________．
三、解答题（本大题共2小题，共20分）
13．设某几何体的三视图如图(尺寸的长度单位为)，
（1）用斜二测画法画出该几何体的直观图(不写画法)；
（2）求该几何体最长的棱长.
14．设一正方形纸片边长为4厘米，切去阴影部分所示的四个全等的等腰三角形，剩余为一正方形纸片和四个全等的等腰三角形，沿虚线折起，恰好能做成一个正四棱锥（粘接损耗不计），图中，为正四棱锥底面中心．，
（1）若正四棱锥的棱长都相等，请求出它的棱长并画出它的直观图示意图；
（2）设等腰三角形的底角为，试把正四棱锥的侧面积表示为的函数，并求范围．
专题28 空间几何体的直观图与三视图
一、单选题（本大题共12小题，共60分）
已知一个几何体的正视图和侧视图如图(1)所示，其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图(2)所示)，则此几何体的体积为( )
A. 1B. 2C. 2D. 22
【答案】B
【解析】解：根据直观图可得该几何体的俯视图是一个直角边长分别是2和2的直角三角形，根据三视图可知该几何体是一个三棱锥，且三棱锥的高为3，
所以体积V=13×12×2×2×3=2．
故选B．
正方形O'A'B'C'的边长为1 cm，它是水平放置的一个平面图形的直观图(如图)，则原图形的周长是( )
A. 6 cmB. 8 cmC. (2+32)cmD. (2+23)cm
【答案】B
【解析】解：如图，
OA=1 cm，在Rt△OAB中，OB=22 cm，
∴AB=OA2+OB2=3 cm．
∴四边形OABC的周长为8 cm．
故选B．
一个几何体的三视图如图所示，则该几何体的表面积为( )
A. 3π2+1+32B. 3π+12+32C. 3π+1+32D. 3π+1+32
【答案】C
【解析】解：由三视图可知几何体上部为三棱锥，下部为半球，
三棱锥的底面和2个侧面均为等腰直角三角形，直角边为1，
另一个侧面为边长为2的等边三角形，
半球的直径2r=2，故r=22．
∴S表面积=12×1×1×2+34×(2)2+12×4π×(22)2+π×(22)2−12×1×1=12+32+3π2．
故选：C．
某几何体的三视图如图所示，则该几何体的表面积为( )
A. 3π+4+3B. 3π+5+3C. 52π+6+3D. 52π+4+3
【答案】A
【解析】解：由已知中的三视图可得：该几何体是一个半圆柱和三棱锥的组合体
半圆柱的半径为1高2，所以该组合体的面积
故选A．
已知某几何体的一条棱长为l，该棱在正视图中的投影长为2020，在侧视图与俯视图中的投影长为a与b，且a+b=21011，则l的最小值为( )
A. 20212B. 40422C. 2021D. 2021
【答案】C
【解析】解：如图所示：
设长方体中AB=m，BD为正投影，BE为侧投影，AC为俯视图的投影．
故：BD=2020，BE=a，AC=b，
设AE=x，CE=y，BC=z，
则：x2+y2+z2=l2，x2+y2=b2，y2+z2=a2，x2+z2=2020，
所以2(x2+y2+z2)=a2+b2+2020，
故：2l2=a2+b2+2020，
因为a2+b2≥(a+b)22=2022，
所以2l2≥2022+2020，则l≥2021．
故l的最小值为2021．
故选C．
已知一几何体的三视图如图所示，则该几何体的表面积为( )
A. 24π+72B. 24π+4C. 1+24π+72D. 1+24π+4
【答案】D
【解析】解：几何体左边为四分之一圆锥，圆锥的半径为1，高为1，右边为三棱锥，三棱锥底面是直角边长为1和2的直角三角形，高为1，
所以几何体的表面积为：
+12×(2+1)×1+12×2×(5)2−(22)2
，
故选D．
某圆柱的正视图是如图所示的边长为2的正方形，圆柱表面上的点A，B，C，D，F在正视图中分别对应点A，B，C，E，F.其中E，F分别为AB，BC的中点，则异面直线AC与DF所成角的余弦值为( )
A. 13 B. 23 C. 33 D. 63
【答案】D
【解析】解：如图所示，连结DE，EF，易知EF//AC，所以异面直线AC与DF所成角为∠DFE，
由正视图可知，DE⊥平面ABC，所以DE⊥EF．
由于AB=BC=2，所以EF=2，又DE=1，所以DF=3，
在RtΔEFM中，cs∠DFE=23=63，
故选D．
如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为( )
A. 22π3 B. 28π3 C. 34π3 D. 40π3
【答案】C
【解析】解：根据几何体得三视图转换为几何体为：
该几何体是由一个底面半径为2，高为3的半圆柱和一个半径为2的半球组成，
故：V=12⋅π×22×3+12×43×π×23=34π3．
故选C．
如图，网络纸上小正方形的边长为1，粗实线画出的某几何体的三视图，则该几何体的体积是( )
A. 18πB. 21πC. 27πD. 36π
【答案】A
【解析】解：该几何体是一个四分之一的圆和圆锥的组合体，如图：
有题意知该圆的直径为6cm，圆锥的高为3cm，则该几何体的体积为13×π×32×3+14×43π×33=18π，
故选A．
如图所是某一容器三视图，现容中匀速注水，容器中的度h随时间变可能图象是( )
A. B. C. D.
【答案】B
【解析】解：三视图表示的容器倒的圆锥，下细，上面，
刚开始度增加的相快些．曲越竖直”，后，高度增加来越慢，图越平稳．
故B．
如图是一个四棱锥的三视图，则该几何体的体积为( )
A. 403B. 323C. 163D. 283
【答案】A
【解析】解：由三视图得到其直观图(下图所示)，
则体积为：13×[12(1+4)×4]×4=403，
故选A ．

如图所示，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为
A. 64−82π3 B. 64−42π3 C. 64−8π3 D. 64−4π3
【答案】A
【解析】解：这是一个有一条侧棱垂直于底面的四棱锥内部挖去了一个八分之一的球，
四棱锥的底面边长和高都等于4，八分之一球的半径为22，
，
故选A．

二、单空题（本大题共4小题，共20分）
某组合体的正视图和侧视图如图(1)所示，它的俯视图的直观图是图(2)中粗线所表示的平面图形，其中四边形O'A'B'C'为平行四边形，D'为C'B'的中点，则图(2)中平行四边形O'A'B'C'的面积为___________．
【答案】32
【解析】解：由正视图和侧视图可得俯视图如下：
∴O'A'=4，O'C'=32，∠A'O'C'=45°，∴SΔA'O'C'=12O'A'·O'C'·sin∠A'O'C'
=12×4×32×22=322，
∴S▱O'A'B'C'=2S△A'O'C'=32，
故答案为32．
以图①为正视图，在图②③④⑤中选两个分别作为侧视图和附视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为_____________(写出符合求的一组答案即可)．
【答案】②⑤或③④
【解析】解：由高度可知，侧视图只能为②或③，
侧视图为②，如图(1)平面PAC⊥平面ABC，PA=PC=2，
BA=BC=5,AC=2，俯视图为⑤；
侧视图为③，如图(2)，PA⊥平面ABC，
PA=1,AC=AB=5,BC=2，俯视图为④．
故答案为②⑤或③④．
在棱长为1的正方体ABCD−A1B1C1D1中，点M，N分别是棱B1C1，C1D1的中点，过A，M，N三点作正方体的截面，将截面多边形向平面ADD1A1作投影，则投影图形的面积为 ．
【答案】712
【解析】解：直线MN分别与直线A1D1，A1B1交于E，F两点，
连接AE，AF，分别与棱DD1，BB1交于G，H两点，连接GN，MH，
得到截面五边形AGNMH，
向平面ADD1A1作投影，得到五边形AH1M1D1G，
由点M，N分别是棱B1C1，C1D1的中点，可得D1E=D1N=12，
由△D1EG∽△DAG，可得DG=2D1G=23，
同理BH=2B1H=23，
则AH1=2A1H1=23，A1M1=D1M1=12，
则SAH1M1D1G=1−SA1H1M1−SADG=1−12×12×13−12×1×23=712，
故答案为：712．
把平面图形α上的所有点在另一个平面上的射影所构成的图形β称为图形α在这个平面上的射影，如图所示，在三棱锥A−BCD中，BC⊥DC，AD⊥DC，BC⊥AB，BC=CD=4，AC=43，则△ADB在平面ABC上的射影的面积是________．
【答案】82
【解析】解：因为BC⊥DC，AD⊥DC，BC⊥AB，BC=CD=4，AC=43，
把三棱锥A−BCD放入如图所示的棱长为4的正方体中，
过点D作CE的垂线DF，垂足为F，连接AF，BF，
因为BC⊥平面CE，DF⊂平面CE，
故BC⊥DF
又BC∩CE=C，BC，CE⊂平面ABC
则DF⊥平面ABC，
故△ADB在平面ABC上的射影为△AFB，
因为AB=42+42=42，
所以△AFB的面积为12×4×42=82，
即△ADB在平面ABC上的射影的面积为82．
故答案为82．
三、解答题（本大题共2小题，共20分）
13．设某几何体的三视图如图(尺寸的长度单位为)，
（1）用斜二测画法画出该几何体的直观图(不写画法)；
（2）求该几何体最长的棱长.
【答案】（1）答案见解析；（2）4.
【解析】（1）
（2）如下图，面，线段中点为，，，
在等腰中，
在中，
在中，
在中，
面，
在中，
在三梭锥S-ABC中，，
所以最长的棱为AC，长为4
14．设一正方形纸片边长为4厘米，切去阴影部分所示的四个全等的等腰三角形，剩余为一正方形纸片和四个全等的等腰三角形，沿虚线折起，恰好能做成一个正四棱锥（粘接损耗不计），图中，为正四棱锥底面中心．，
（1）若正四棱锥的棱长都相等，请求出它的棱长并画出它的直观图示意图；
（2）设等腰三角形的底角为，试把正四棱锥的侧面积表示为的函数，并求范围．
【答案】（1），画图见解析；（2），.
【解析】（1）由题意，设正四棱锥的棱长为，则，
，
（2）设，则，由，可得，
从而，其中，
∴