

所属成套资源:2023-2024学年浙江省宁波市各区八年级(上)期中数学试卷
2023-2024学年浙江省宁波市北仑区精准联盟九年级(上)期中数学试卷
展开
这是一份2023-2024学年浙江省宁波市北仑区精准联盟九年级(上)期中数学试卷,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.(3分)“明天是晴天”这个事件是( )
A.确定事件B.不可能事件
C.必然事件D.不确定事件
2.(3分)抛物线y=﹣2(x﹣2)2﹣5的顶点坐标是( )
A.(﹣2,5)B.(2,5)C.(﹣2,﹣5)D.(2,﹣5)
3.(3分)如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段,则线段AB的长是( )
A.B.2C.D.5
4.(3分)如果线段a=2,c=8,那么线段a和c的比例中项b是( )
A.4B.16C.±4D.±16
5.(3分)如图,已知AB是⊙O的直径,CD是弦,若∠BCD=24°,则∠ABD=( )
A.54°B.56°C.64°D.66°
6.(3分)在Rt△ABC中,∠ACB=90°,AC=6,AB=10,以C为圆心,BC为半径作⊙C,则点A与⊙C的位置关系是( )
A.点A在⊙C内B.点A在⊙C上C.点A在⊙C外D.无法确定
7.(3分)对于二次函数y=x2﹣4x﹣1的图象,下列说法错误的是( )
A.开口向上
B.与x轴有两个交点
C.抛物线的对称轴为直线x=2
D.当x≥2时,y随x的增大而减小
8.(3分)下列有关圆的一些结论:①平分弧的直径垂直于弧所对的弦;②平分弦的直径垂直于弦;③在同圆或等圆中,相等的弦所对的圆周角相等;④同弧或等弧所对的弦相等,其中正确的有( )
A.①④B.②③C.①③D.②④
9.(3分)如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
A.DE=EBB.DE=EBC.DE=DOD.DE=OB
10.(3分)已知抛物线y=(x﹣b)2+c经过A(1﹣n,y1),B(n,y2),C(n+3,y3)三点,y1=y3.当1﹣n≤x≤n时,二次函数的最大值与最小值的差为16,则n的值为( )
A.﹣5B.3C.D.4
二、填空题:本题有6个小题,每小题4分,共24分.
11.(4分)如图,转盘被分成5个面积相等的扇形,任意转动这个转盘1次,当转盘停止转动时,指针落在阴影区域的概率为 .
12.(4分)如图,四边形ABCO的顶点A、B、C在⊙O上,若∠ABC=130°,则∠AOC= .
13.(4分)已知点E是线段AB的黄金分割点,且BE>AE,若AB=2,则BE= .
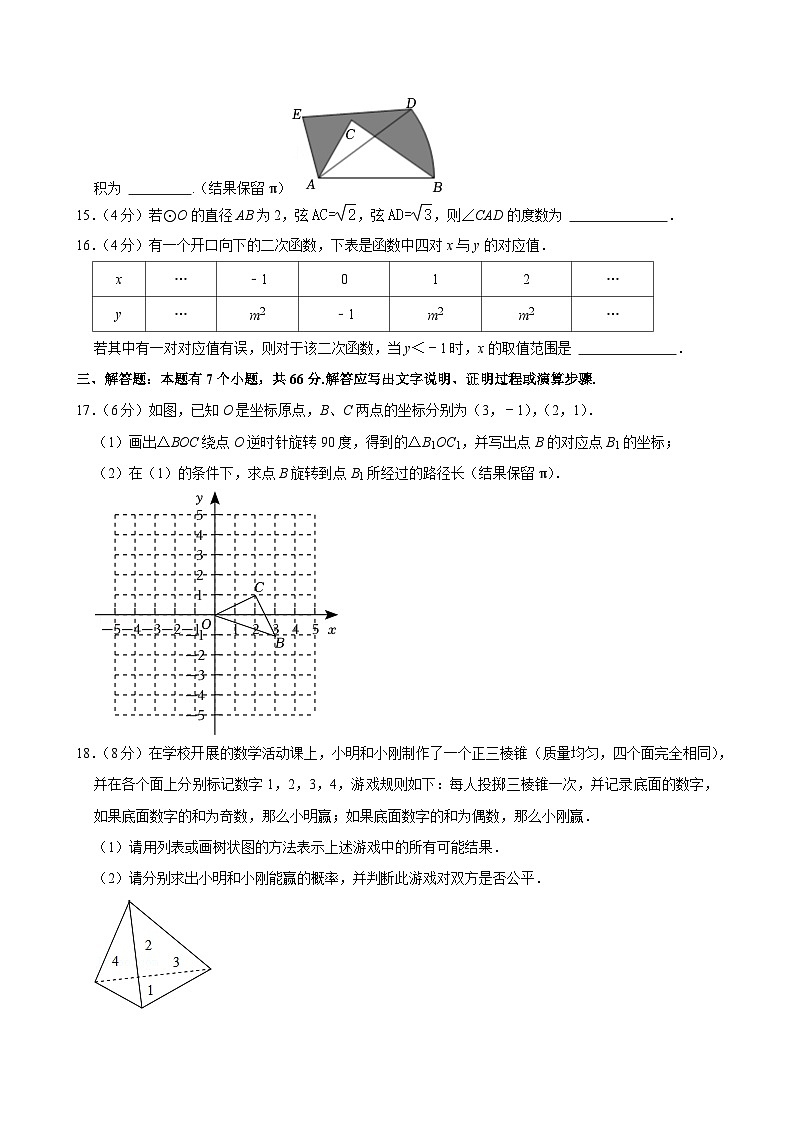
14.(4分)如图,将△ABC绕点A逆时针旋转45°后得到△ADE.若AB=4,则图中阴影部分图形的面积为 .(结果保留π)
15.(4分)若⊙O的直径AB为2,弦,弦,则∠CAD的度数为 .
16.(4分)有一个开口向下的二次函数,下表是函数中四对x与y的对应值.
若其中有一对对应值有误,则对于该二次函数,当y<﹣1时,x的取值范围是 .
三、解答题:本题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1),(2,1).
(1)画出△BOC绕点O逆时针旋转90度,得到的△B1OC1,并写出点B的对应点B1的坐标;
(2)在(1)的条件下,求点B旋转到点B1所经过的路径长(结果保留π).
18.(8分)在学校开展的数学活动课上,小明和小刚制作了一个正三棱锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下:每人投掷三棱锥一次,并记录底面的数字,如果底面数字的和为奇数,那么小明赢;如果底面数字的和为偶数,那么小刚赢.
(1)请用列表或画树状图的方法表示上述游戏中的所有可能结果.
(2)请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.
19.(8分)已知二次函数y=ax2+bx﹣3的图象经过点A(2,﹣3),B(﹣1,0).
(1)求二次函数的解析式;
(2)要使该二次函数的图象与x轴只有一个交点,应把图象向上平移几个单位?
20.(10分)如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
21.(10分)已知AB是⊙O的直径,点C在⊙O上,D为弧BC的中点.
(1)如图①,连接AC,AD,OD.求证:OD∥AC;
(2)如图②,过点D作DE⊥AB交⊙O于点E,直径EF交AC于点G,若G为AC中点,
①求证:∠BOD=45°;
②若⊙O的半径为2,求AC的长.
22.(12分)某商家代理经销某种商品,以每件进价40元,批发购进该商品915件,经走访市场发现:每天的销售量y(件)和销售单价x之间的一次函数关系如下表(x≥50的整数).
(1)写出y关于x的函数关系式 .
(2)问定价x为多少时,每天获得利润最大,并求最大利润.
(3)商家在实际销售过程中,以每天最大利润销售了10天后,他发现销售时间只剩下最后两天,所以在最后不超过2天时间内销售完余下的商品,这915件商品的总利润为w元,则总利润w的最大值为 (直接写出答案).
23.(12分)如图,AB为⊙O的直径,点C、D都在⊙O上,且CD平分∠ACB,交AB于点E.
(1)求证:∠ABD=∠BCD;
(2)若DE=13,AE=17,求⊙O的半径;
(3)DF⊥AC于点F,试探究线段AF、DF、BC之间的数量关系,并说明理由.
2023-2024学年浙江省宁波市北仑区精准联盟九年级(上)期中数学试卷
参考答案与试题解析
一、选择题:本题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项最符合题目要求.
1.(3分)“明天是晴天”这个事件是( )
A.确定事件B.不可能事件
C.必然事件D.不确定事件
【分析】在一定条件下,可能发生也可能不发生的事件,称为随机事件.
【解答】解:“明天是晴天”这个事件是随机事件,属于不确定事件,
故选:D.
【点评】本题主要考查了必然事件、不可能事件、随机事件的概念.事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,必然事件和不可能事件都是确定的.
2.(3分)抛物线y=﹣2(x﹣2)2﹣5的顶点坐标是( )
A.(﹣2,5)B.(2,5)C.(﹣2,﹣5)D.(2,﹣5)
【分析】根据二次函数性质,由顶点式直接写出顶点坐标即可.
【解答】解:因为抛物线y=﹣2(x﹣2)2﹣5,
所以抛物线y=﹣2(x﹣2)2﹣5的顶点坐标是(2,﹣5).
故选:D.
【点评】本题考查了二次函数性质,由顶点式直接写出顶点坐标是解题关键.
3.(3分)如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段,则线段AB的长是( )
A.B.2C.D.5
【分析】过点A作平行横线的垂线,交点B所在的平行横线于D,交点C所在平行横线于E,根据平行线分线段成比例定理,列出比例式,计算即可得解.
【解答】解:过点A作平行横线的垂线,交点B所在的平行横线于D,交点C所在平行横线于E,
∴,
∵五线谱是由等距离的五条平行横线组成的,
∴,
∴,
解得AB=5,
故选:D.
【点评】此题考查了平行线分线段成比例定理,熟练掌握并灵活运用该定理、找准对应线段是解答此题的关键.
4.(3分)如果线段a=2,c=8,那么线段a和c的比例中项b是( )
A.4B.16C.±4D.±16
【分析】根据比例中项的定义可得b2=ac,从而易求b.
【解答】解:∵b是a、c的比例中项,
∴b2=ac,
即b2=2×8=16,
b=4(负数舍去).
故选:A.
【点评】本题考查了比例线段,解题的关键是理解比例中项的含义.
5.(3分)如图,已知AB是⊙O的直径,CD是弦,若∠BCD=24°,则∠ABD=( )
A.54°B.56°C.64°D.66°
【分析】根据圆周角定理得到∠ADB=90°,∠A=∠BCD=24°,然后利用互余计算∠ABD的度数.
【解答】解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠A=∠BCD=24°,
∴∠ABD=90°﹣∠A=90°﹣24°=66°.
故选:D.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
6.(3分)在Rt△ABC中,∠ACB=90°,AC=6,AB=10,以C为圆心,BC为半径作⊙C,则点A与⊙C的位置关系是( )
A.点A在⊙C内B.点A在⊙C上C.点A在⊙C外D.无法确定
【分析】利用勾股定理求得BC边的长,然后通过比较AC与半径BC的长即可得到结论.
【解答】解:∵Rt△ABC中,∠ACB=90°,AC=6,AB=10,
∴BC==8,
∵AC=6<BC,
∴点A在⊙C内,
故选:A.
【点评】本题考查了点与圆的位置关系,解题的关键是确定圆的半径和点与圆心之间的距离之间的大小关系.
7.(3分)对于二次函数y=x2﹣4x﹣1的图象,下列说法错误的是( )
A.开口向上
B.与x轴有两个交点
C.抛物线的对称轴为直线x=2
D.当x≥2时,y随x的增大而减小
【分析】根据二次函数的图象和性质分别对抛物线开口方向、与x轴交点个数、顶点坐标、函数的增减性进行判断即可.
【解答】解:A、∵二次函数y=x2﹣4x﹣1中,a=1,则a>0,
∴抛物线开口向上,故选项正确,不符合题意;
B、当y=0时,0=x2﹣4x﹣1,
∵Δ=(﹣4)2﹣4×1×(﹣1)=20>0,
∴方程x2﹣4x﹣1=0有两个不相等的实数根,则二次函数y=x2﹣4x﹣1的图象与x轴有两个交点,故选项正确,不符合题意;
C、∵y=x2﹣4x﹣1=(x﹣2)2﹣5,
∴抛物线的对称轴为x=2,故选项正确,不符合题意;
D、∵y=x2﹣4x﹣1=(x﹣2)2﹣5,
∴抛物线的对称轴是直线x=2,
∵a=1>0,
∴抛物线开口向上,
∴当x≥2时,y随x的增大而增大,故选项错误,符合题意.
故选:D.
【点评】此题考查了二次函数的图象和性质,熟练掌握二次函数的图象和性质是解题的关键.
8.(3分)下列有关圆的一些结论:①平分弧的直径垂直于弧所对的弦;②平分弦的直径垂直于弦;③在同圆或等圆中,相等的弦所对的圆周角相等;④同弧或等弧所对的弦相等,其中正确的有( )
A.①④B.②③C.①③D.②④
【分析】利用等弧的定义、圆周角定理、垂径定理及其推理分别判断后即可确定正确的选项.
【解答】解:①平分弧的直径垂直于弧所对的弦,故正确;
②平分弦(不是直径)的直径垂直于弦,故错误;
③在同圆或等圆中,相等的弦对应的圆周角相等或互补,故错误;
④同弧或等弧所对的弦相等;故正确;
正确的有2个,
故选:A.
【点评】本题考查了命题与定理的知识,解题的关键是了解垂径定理、等弧的定义,圆周角定理等知识,难度不大.
9.(3分)如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
A.DE=EBB.DE=EBC.DE=DOD.DE=OB
【分析】连接EO,只要证明∠D=∠EOD即可解决问题.
【解答】解:连接EO.
∵OB=OE,
∴∠B=∠OEB,
∵∠OEB=∠D+∠DOE,∠AOB=3∠D,
∴∠B+∠D=3∠D,
∴∠D+∠DOE+∠D=3∠D,
∴∠DOE=∠D,
∴ED=EO=OB,
故选:D.
【点评】本题考查圆的有关知识、三角形的外角等知识,解题的关键是添加除以辅助线,利用等腰三角形的判定方法解决问题,属于中考常考题型.
10.(3分)已知抛物线y=(x﹣b)2+c经过A(1﹣n,y1),B(n,y2),C(n+3,y3)三点,y1=y3.当1﹣n≤x≤n时,二次函数的最大值与最小值的差为16,则n的值为( )
A.﹣5B.3C.D.4
【分析】根据y1=y3,可得A,C两点关于对称轴对称,从而得到抛物线解析式为y=(x﹣2)2+c,再由1﹣n≤x≤n,可得点B在点A的右侧,,然后分两种情况讨论,即可求解.
【解答】解:∵y1=y3,
∴A,C两点关于对称轴对称.
∴,
即抛物线解析式为y=(x﹣2)2+c.
∵1﹣n≤x≤n,
∴点B在点A的右侧,且有1﹣n≤n,
∴.
情况1:如图1,当点A与点B均在对称轴的左侧时,此时n<2;
当x=1﹣n时,二次函数取到最大值为y=(1﹣n﹣2)2+c=(n+1)2+c;
当x=n时,二次函数取到最小值为y=(n﹣2)2+c,
∴(n+1)2+c﹣(n﹣2)2﹣c=16,解得(舍去).
情况2:如图2,当点A与点B在对称轴的两侧时,此时n≥2;A到对称轴的水平距离为2﹣(1﹣n)=1+n.B到对称轴的距离为n﹣2,当x=1﹣n时,二次函数取到最大值为y=(1﹣n﹣2)2+c=(n+1)2+c;
当x=2时,二次函数取到最小值为y=c,
∴(n+1)2+c﹣c=16,解得n=3或﹣5(舍).
综上,n=3.
故选:B.
【点评】本题主要考查了二次函数的图象和性质,熟练掌握二次函数的图象和性质,利用分类讨论思想解答是解题的关键.
二、填空题:本题有6个小题,每小题4分,共24分.
11.(4分)如图,转盘被分成5个面积相等的扇形,任意转动这个转盘1次,当转盘停止转动时,指针落在阴影区域的概率为 .
【分析】首先确定在图中阴影区域的面积在整个面积中占的比例,根据这个比例即可求出指针指向阴影区域的概率.
【解答】解:∵转盘被分成5个面积相等的扇形,其中阴影部分占2份,
∴指针落在阴影区域的概率为,
故答案为:.
【点评】本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A),然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.
12.(4分)如图,四边形ABCO的顶点A、B、C在⊙O上,若∠ABC=130°,则∠AOC= 100° .
【分析】首先在优弧AC上取点D,连接AD,CD,由圆的内接四边形的性质,可求得∠ADC的度数,然后由圆周角定理,求得∠AOC的度数.
【解答】解:如图,在优弧AC上取点D,连接AD,CD,
∵∠ABC=130°,
∴∠ADC=180°﹣∠ABC=50°,
∴∠AOC=2∠ADC=100°.
故答案为:100°.
【点评】此题考查了圆周角定理以及圆的内接四边形的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
13.(4分)已知点E是线段AB的黄金分割点,且BE>AE,若AB=2,则BE= ﹣1 .
【分析】根据黄金分割点的定义求解.
【解答】解:∵E是线段AB的黄金分割点,且BE>AE,
∴,
BE===﹣1,
故答案为﹣1.
【点评】此题考查了黄金分割点的概念,要熟记黄金比的值.
14.(4分)如图,将△ABC绕点A逆时针旋转45°后得到△ADE.若AB=4,则图中阴影部分图形的面积为 2π .(结果保留π)
【分析】根据旋转的性质可得△AED≌△ACB,再由S阴影=S△AED+S扇形DAB﹣S△ACB=S扇形DAB,利用扇形的面积公式求解即可.
【解答】解:由旋转的性质可得:△AED≌△ACB,
∵∠DAB=45°,AB=4,
∴S扇形DAB==2π,
∴S阴影=S△AED+S扇形DAB﹣S△ACB=S扇形DAB=2π.
故答案为:2π.
【点评】本题考查不规则阴影部分面积的求法及扇形的面积公式,熟练掌握扇形的面积公式是解题的关键.
15.(4分)若⊙O的直径AB为2,弦,弦,则∠CAD的度数为 15°或75° .
【分析】本题大致的思路是连接BC、BD,分别在Rt△CAB和Rt△BAD中,求出∠CAD和∠CAB的度数,然后根据C点,D点的不同位置分类讨论.
【解答】解:本题分两种情况:(如图)
①当AC,AD在AB同侧时,连接BD、BC;
则∠ADB=∠ACB=90°.
Rt△ADB中,AD=,AB=2;
∴∠DAB=30°;
Rt△ACB中,AC=,AB=2;
∴∠CAB=45°;
∴∠CAD=∠CAB﹣∠DAB=15°.
②当AC,AD在AB异侧时,同①可求得∠CAD=75°.
故∠CAD的度数为15°或75°.
故答案为:15°或75°.
【点评】本题考查的是圆周角定理及直角三角形的性质,比较简单,但在解答时要注意分两种情况讨论,不要漏解.
16.(4分)有一个开口向下的二次函数,下表是函数中四对x与y的对应值.
若其中有一对对应值有误,则对于该二次函数,当y<﹣1时,x的取值范围是 x<0或x>3 .
【分析】根据抛物线开口向下及抛物线的增减性即可求解.
【解答】解:∵x=0时y的值小于x=﹣1、1、2时y的值,
∵抛物线开口向下,
∴抛物线必为先递增再递减,
∴x=﹣1时y的值错误数据;
又∵x=1和2时y的值相等,
∴抛物线对称轴为,
∴x=0和3时y的值相等,为﹣1,
∴当y<﹣1时,x<0或x>3.
故答案为:x<0或x>3.
【点评】本题考查二次函数的性质,二次函数图象上点的坐标特征,解题关键是掌握二次函数的性质.
三、解答题:本题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1),(2,1).
(1)画出△BOC绕点O逆时针旋转90度,得到的△B1OC1,并写出点B的对应点B1的坐标;
(2)在(1)的条件下,求点B旋转到点B1所经过的路径长(结果保留π).
【分析】(1)根据旋转的性质作图,即可得出答案.
(2)利用勾股定理求出OB的长,再利用弧长公式计算即可.
【解答】解:(1)如图,△B1OC1即为所求.
点B1的坐标为(1,3).
(2)由勾股定理得,,
∴点B旋转到点B1所经过的路径长为=.
【点评】本题考查作图﹣旋转变换、弧长公式,熟练掌握旋转的性质、弧长公式是解答本题的关键.
18.(8分)在学校开展的数学活动课上,小明和小刚制作了一个正三棱锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下:每人投掷三棱锥一次,并记录底面的数字,如果底面数字的和为奇数,那么小明赢;如果底面数字的和为偶数,那么小刚赢.
(1)请用列表或画树状图的方法表示上述游戏中的所有可能结果.
(2)请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.
【分析】(1)根据题意在表格内列举出所有情形;
(2)根据题意列出表格,找出所有等可能的情况数,得出两球数字和为奇数与偶数的情况,分别求出两人获胜得概率,比较即可得到游戏公平与否.
【解答】解:(1)列表如下:
(2)从图表可知,共有16种等可能的情况,其中两次所掷数字的和为奇数的情况有8种,和为偶数的有8种,
所以小明获胜的概率为、小刚获胜的概率为,
故此游戏对两人是公平的.
【点评】本题考查了游戏的公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.也考查了列表法与树状图法.
19.(8分)已知二次函数y=ax2+bx﹣3的图象经过点A(2,﹣3),B(﹣1,0).
(1)求二次函数的解析式;
(2)要使该二次函数的图象与x轴只有一个交点,应把图象向上平移几个单位?
【分析】(1)把A点和B点坐标代入y=ax2+bx﹣3得到关于a、b的方程组,然后解方程组即可.
(2)求得顶点坐标,根据题意即可求得结论.
【解答】解:(1)由题意得,,
解得,
∴所求的二次函数的解析式为y=x2﹣2x﹣3;
(2)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为(1,4),
∵二次函数的图象与x轴只有一个交点,
∴应把图象向上平移4个单位.
【点评】本题考查了待定系数法求二次函数的解析式,二次函数的图象与几何变换,能够正确理解题意是解题的关键.
20.(10分)如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
【分析】(1)连接OA,利用r表示出OD的长,在Rt△AOD中根据勾股定理求出r的值即可;
(2)连接OA′,在Rt△A′EO中,由勾股定理得出A′E的长,进而可得出A′B′的长,据此可得出结论.
【解答】解:(1)连接OA,
由题意得:AD=AB=30(米),OD=(r﹣18)米,
在Rt△ADO中,由勾股定理得:r2=302+(r﹣18)2,
解得,r=34(米);
(2)连接OA′,
∵OE=OP﹣PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2﹣OE2,即:A′E2=342﹣302,
解得:A′E=16(米).
∴A′B′=32(米).
∵A′B′=32>30,
∴不需要采取紧急措施.
【点评】本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
21.(10分)已知AB是⊙O的直径,点C在⊙O上,D为弧BC的中点.
(1)如图①,连接AC,AD,OD.求证:OD∥AC;
(2)如图②,过点D作DE⊥AB交⊙O于点E,直径EF交AC于点G,若G为AC中点,
①求证:∠BOD=45°;
②若⊙O的半径为2,求AC的长.
【分析】(1)根据圆周角定理,由=得到∠BAD=∠CAD,加上∠BAD=∠ODA,所以∠CAD=∠ODA,然后根据平行线的判定方法得到结论;
(2)①先根据垂径定理得到EF⊥AC,再利用OD∥AC得到DO⊥EF,所以∠DOE=90°,接着利用垂径定理得到=,然后根据圆周角定理得到∠BOD=∠DOE=45°;
②由OD∥AC得到∠CAB=∠BOD=45°,再根据垂径定理得到AG=CG,然后根据等腰直角三角形的性质求出AG=,从而得到AC的长.
【解答】(1)证明:∵D为弧BC的中点,
∴=,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠BAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC;
(2)解:①∵G为AC中点,EF为直径,
∴EF⊥AC,
∵OD∥AC,
∴DO⊥EF,
∴∠DOE=90°,
∵AB是⊙O的直径,DE⊥AB,
∴=,
∴∠BOD=∠DOE=45°;
②∵OD∥AC,
∴∠CAB=∠BOD=45°,
∵OG⊥AC,
∴AG=CG,△AOG是等腰直角三角形,
∴AG=×2=,
∴AC=2AG=2.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.
22.(12分)某商家代理经销某种商品,以每件进价40元,批发购进该商品915件,经走访市场发现:每天的销售量y(件)和销售单价x之间的一次函数关系如下表(x≥50的整数).
(1)写出y关于x的函数关系式 y=﹣5x+350 .
(2)问定价x为多少时,每天获得利润最大,并求最大利润.
(3)商家在实际销售过程中,以每天最大利润销售了10天后,他发现销售时间只剩下最后两天,所以在最后不超过2天时间内销售完余下的商品,这915件商品的总利润为w元,则总利润w的最大值为 13475元 (直接写出答案).
【分析】(1)利用表格中的数据,待定系数法求解析式即可;
(2)设每天的利润为z元,根据总利润等于单件利润乘以销售数量,求出函数解析式,求最值即可;
(3)先求出前10天的利润以及卖出的数量,再根据二次函数的性质,得到后两天的定价分别为54元和53元时,刚好卖完,利润最大,即可得解.
【解答】解:(1)设y关于x的函数关系式为:y=kx+b,
则:由表格可知:,解得:,
∴y=﹣5x+350;
故答案为:y=﹣5x+350.
(2)设每天的利润为z元,
则:z=(x﹣40)(﹣5x+350)=﹣5(x﹣55)2+1125;
∵a=﹣5<0,
∴当x=55时,每天获得的利润最大,最大利润为1125元,
即:定价为55元时,每天获得的利润最大,最大利润为1125元;
(3)以每天最大销售利用销售10天,获利为:10×1125=11250(元);
卖出商品的数量为:(﹣5×55+350)×10=750件,还剩下:915﹣750=165(件),
∵z=﹣5(x﹣55)2+1125,
∴当定价离55元越近时,每天的利润就越大,
∵在最后不超过2天时间内销售完余下的商品,x是大于等于50的整数,
当定价为:54元时,销售数量为:y=﹣5×54+350=80(件),
当定价为:53元时,销售数量为:y=﹣5×53+350=85(件),80+85=165(件),
∴最后两天的最大利润为:(54﹣40)×80+(53﹣40)×85=2225(元),
∴总利润w的最大值为:11250+2225=13475(元).
故答案为:13475元.
【点评】本题考查二次函数的应用.利用总利润等于单件利润乘以销售数量,正确的列出二次函数解析式,是解题的关键.
23.(12分)如图,AB为⊙O的直径,点C、D都在⊙O上,且CD平分∠ACB,交AB于点E.
(1)求证:∠ABD=∠BCD;
(2)若DE=13,AE=17,求⊙O的半径;
(3)DF⊥AC于点F,试探究线段AF、DF、BC之间的数量关系,并说明理由.
【分析】(1)由CD平分∠ACB,根据圆周角定理,可得∠ACD=∠BCD=∠ABD;
(2)过点E作EM⊥AD于点M,求出AD长,则AB=AD,可求出AB;则答案得出;
(3)过点D作DN⊥CB,交CB的延长线于点N,可证明△DAF≌△DBN,则AF=BN,DF=CF则结论AF+BC=DF可得出.
【解答】(1)证明:∵CD平分∠ACB,
∴∠ACD=∠BCD,
∵∠ACD=∠ABD,
∴∠ABD=∠BCD;
(2)解:如图1,过点E作EM⊥AD于点M,
∵AB为⊙O的直径,
∴∠ACB=90°,∠ADB=90°,
∴∠DAB=∠BCD=45°,
∵AE=17,
∴ME=AM=17×=,
∵DE=13,
∴DM===,
∴AD=AM+DM=12,
∴AB=AD=12=24,
∴AO==12;
(3)AF+BC=DF.理由如下:
如图2,过点D作DN⊥CB,交CB的延长线于点N,
∵四边形DACB内接于圆,
∴∠DBN=∠DAF,
∵DF⊥AC,DN⊥CB,CD平分∠ACB,
∴∠AFD=∠DNB=90°,DF=DN,
∴△DAF≌△DBN(AAS),
∴AF=BN,CF=CN,
∵∠FCD=45°,
∴DF=CF,
∴CN=BN+BC=AF+BC=DF.
即AF+BC=DF.
【点评】此题考查了和圆有关的综合性题目,考查了等腰直角三角形的判定与性质、圆内接四边形的性质、圆周角定理、角平分线的性质、全等三角形的判定与性质以及勾股定理,熟练掌握圆的有关性质定理是解题的关键.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2024/10/18 14:04:34;用户:周静;邮箱:yjpxxx05@xyh.cm;学号:30479237x
…
﹣1
0
1
2
…
y
…
m2
﹣1
m2
m2
…
销售单价x(元/件)
…
50
51
52
…
每天销售量y(件)
…
100
95
90
…
x
…
﹣1
0
1
2
…
y
…
m2
﹣1
m2
m2
…
1
2
3
4
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
销售单价x(元/件)
…
50
51
52
…
每天销售量y(件)
…
100
95
90
…
相关试卷
这是一份2023-2024学年浙江省宁波市北仑区精准联盟七年级(上)期中数学试卷及解析(word版,含答案),文件包含2023-2024学年浙江省宁波市北仑区精准联盟七年级上期中数学试卷解析docx、2023-2024学年浙江省宁波市北仑区精准联盟七年级上期中数学试卷docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
这是一份浙江省宁波市北仑区精准联盟2023-—2024学年七年级下学期4月期中数学试题,共4页。
这是一份浙江省宁波市北仑区精准联盟2023-2024年八年级下学期期中数学试题(原卷版+解析版),文件包含浙江省宁波市北仑区精准联盟2023-2024年八年级下学期期中数学试题原卷版docx、浙江省宁波市北仑区精准联盟2023-2024年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。








