第02讲 等式与不等式（含答案） 备战2025年高考数学一轮复习考点帮（天津专用）学案

这是一份第02讲 等式与不等式（含答案） 备战2025年高考数学一轮复习考点帮（天津专用）学案，文件包含第02讲等式与不等式教师版备战2025年高考数学一轮复习考点帮天津专用docx、第02讲等式与不等式学生版备战2025年高考数学一轮复习考点帮天津专用docx等2份学案配套教学资源，其中学案共36页， 欢迎下载使用。

1. 5年真题考点分布
2. 命题规律及备考策略
【命题规律】本节内容是天津高考卷的必考内容，设题稳定，难度为低难度与中档难度，分值为5分
【备考策略】1.理解、掌握不等式的性质，能够运用不等式的性质进行比较大小
2.能掌握一元二次不等式的性质
3.掌握一元二次不等式根与系数的关系
4.会解一元二次不等式、能够解决一元二不等式的恒成立与存在成立等问题
【命题预测】本节内容是天津高考卷的必考内容，一般考查不等式的性质，一元二次不等式的性质等。
知识讲解
知识点一.等式与不等式的性质:
1.两个实数比较大小的方法
(1)作差法
a-b >0⟺ a>b，
a-b =0⟺ a=b,
a-b 0⟺a>ba∈R,b>0,
ab=1a,b≠0⟺a=ba,b≠0,
ab0⟺a0,
2.等式的性质
(1)对称性:若a=b，则b=a.
(2)传递性:若a=b，b=c，则a=c.
(3)可加性:若a=b，则a+c =b+c.
(4)可乘性:若a=b，则ac=bc;若a =b，c=d，则ac=bd
3.不等式的性质
(1)对称性: a>b ⟺ bb，b>c⟺ a>c;
(3)可加性a>b ⟺a+c>b+c; a>b, c>d ⟺a+c>b+d
(4)可乘性: a>b, c >0⟺ac>bc; a>b, c 0，c>d>0⟺ ac>bd;
(5)可乘方: a>b>0⟺an>bn(n∈N，n≥1);
(6)可开方a>b>0⟺ na>nb(n∈N，n≥2).
知识点二.一元二次不等式
1.一元二次不等式的概念
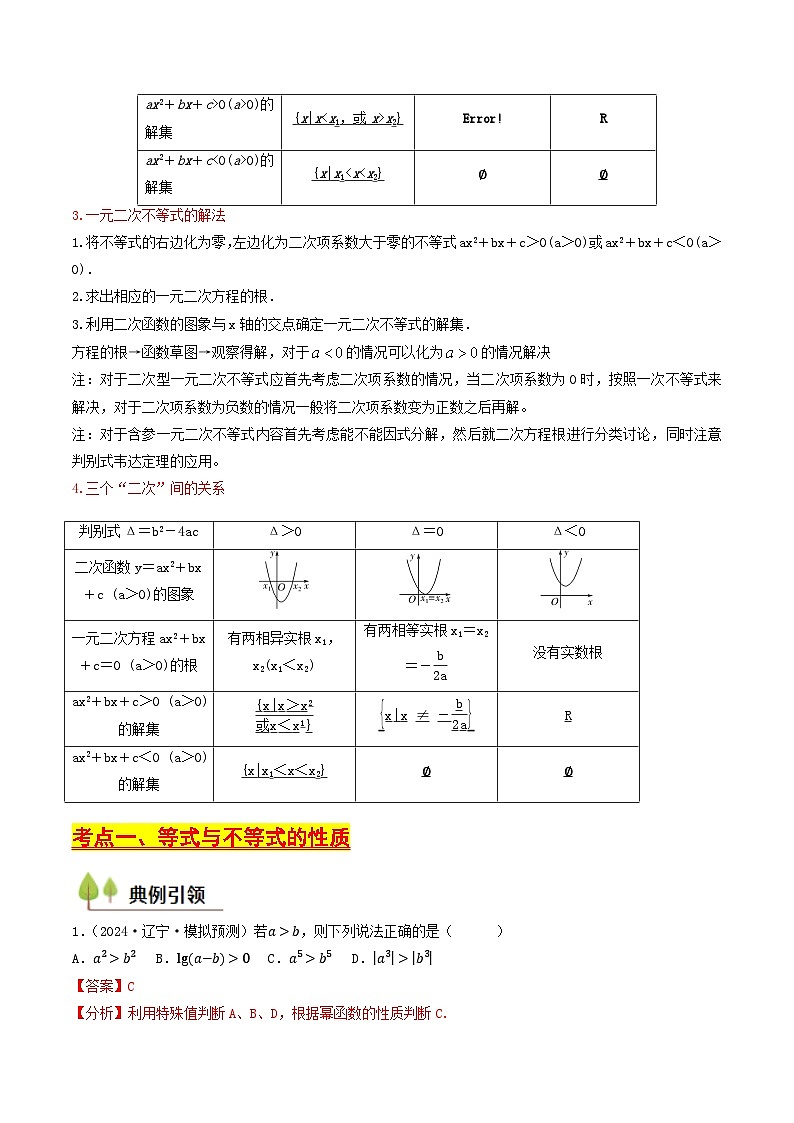
2.二次函数与一元二次方程的根、一元二次不等式的解集的对应关系
3.一元二次不等式的解法
1.将不等式的右边化为零，左边化为二次项系数大于零的不等式ax2＋bx＋c＞0(a＞0)或ax2＋bx＋c＜0(a＞0)．
2.求出相应的一元二次方程的根．
3.利用二次函数的图象与x轴的交点确定一元二次不等式的解集．
方程的根→函数草图→观察得解，对于的情况可以化为的情况解决
注：对于二次型一元二次不等式应首先考虑二次项系数的情况，当二次项系数为0时，按照一次不等式来解决，对于二次项系数为负数的情况一般将二次项系数变为正数之后再解。
注：对于含参一元二次不等式内容首先考虑能不能因式分解，然后就二次方程根进行分类讨论，同时注意判别式韦达定理的应用。
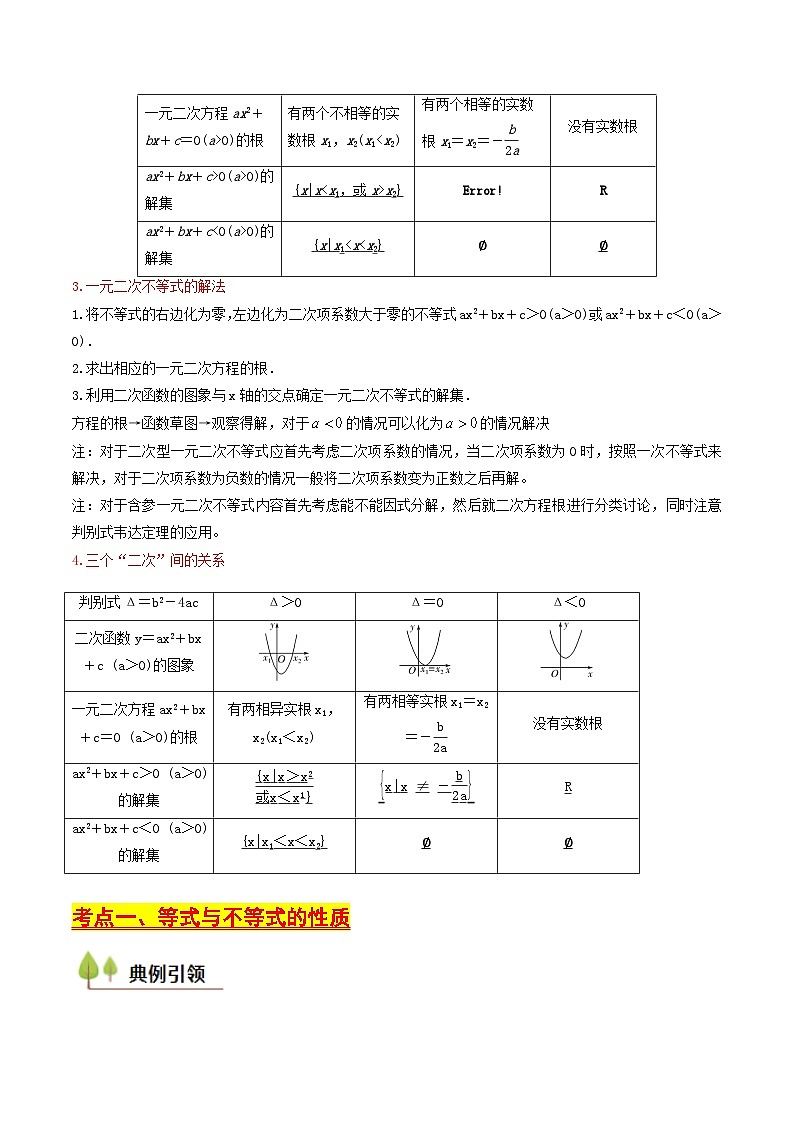
4.三个“二次”间的关系
考点一、等式与不等式的性质
1．（2024·辽宁·模拟预测）若a>b，则下列说法正确的是（ ）
A．a2>b2B．lg(a−b)>0C．a5>b5D．a3>b3
【答案】C
【分析】利用特殊值判断A、B、D，根据幂函数的性质判断C.
【详解】对于A：当a=0、b=−1，满足a>b，但是a2b，但是lg(a−b)=lg1=0，故B错误；
对于C：因为y=x5在定义域R上单调递增，若a>b，则a5>b5，故C正确
对于D：当a=1、b=−1，满足a>b，但是a3=b3，故D错误.
故选：C
2．（2024·山东滨州·二模）下列命题中，真命题的是（ ）
A．若a>b，则ac>bcB．若a>b，则a2>b2
C．若ac2≥bc2，则a≥bD．若a+2b=2，则2a+4b≥4
【答案】D
【分析】由不等式的性质可判断A,B,C，利用基本不等式a+b≥2ab，当且仅当a=b时等号成立，即可判断D.
【详解】对于A，由a>b，c=0可得ac=bc，故A错误；
对于B，由a>0，b＜0，a＜b，可得a2＜b2，故B错误；
对于C，若ac2≥bc2，且当c=0时，可得a，b为任意值，故C错误；
对于D，因为2a+4b=2a+22b≥22a⋅22b=22a+2b=4，当且仅当a=2b=1时，等号成立，
即2a+4b≥4，故D正确.
故选：D.
1．（22-23高三上·甘肃定西·阶段练习）已知a>b>0,cbcB．ac>bcC．bc2>ac2D．ab−bc>0
【答案】D
【分析】对于ACD，利用作差法判断，对于B，利用幂函数的性质比较.
【详解】对于A，因为a>b>0,c0
D．若a>b>0，则a+1b>b+1a
【答案】D
【分析】举反例即可推出A,B,C错误，D利用反比例函数单调性和不等式可加性即可证得.
【详解】当a=−1,b=−1时，a+b=−2，所以A错.
当a0时，ab>0，则1b>1a>0，则a+1b>b+1a成立，所以D正确.
故选：D
3.（2024·天津·一模）已知a,b∈R，则“b>a”是“a2a时，有b>a≥0，则a2a”是“a2b⇔a−b>0，因此要比较a，b的大小，作差，通分，利用对数的运算性质，即可求得a，b的大小；利用对数函数y=lnx的单调性，可知ln2π>ln6>0，然后利用不等式的可乘性，即可得出a，c的大小.
【详解】解：a−b=ln264−ln2ln3=ln2+ln32−4ln2ln34=ln2−ln324>0，∴a>b，
而ln2π>ln6>0，∴ln22π4>ln264，即c>a，
因此c>a>b.
故选：C.
2.（2024·四川成都·模拟预测）已知a，b为实数，则使得“a>b>0”成立的一个必要不充分条件为（ ）
A．1a>1bB．ln(a+1)>ln(b+1)
C．a3>b3>0D．a−1>b−1
【答案】B
【分析】利用不等式的性质、结合对数函数、幂函数单调性，充分条件、必要条件的定义判断即得.
【详解】对于A，1a>1b ，不能推出a>b>0，如1−3>1−2，反之a>b>0 ，则有1a1b是a>b>0的既不充分也不必要条件，A错误；
对于B，由lna+1>lnb+1，得a+1>b+1>0，即a>b>−1，
不能推出a>b>0 ，反之a>b>0，则a>b>−1，
因此ln(a+1)>ln(b+1)是a>b>0的必要不充分条件，B正确；
对于C，a3>b3>0⇔a>b>0，a3>b3>0是a>b>0的充分必要条件，C错误；
对于D，由a−1>b−1，得a>b≥1>0，反之a>b>0不能推出a>b≥1，
因此a−1>b−1是a>b>0的充分不必要条件，D错误.
故选：B.
1．（22-23高三上·天津河西·期末）若a，b，c∈R，a>b，则下列不等式成立的是（ ）
A．1abc
【答案】C
【分析】举反例排除ABD，利用不等式的性质判断C即可得解.
【详解】对于A，取a=1,b=−1，满足a>b，但1a>1b，故A错误；
对于B，取a=1,b=−1，满足a>b，但a2=b2，故B错误；
对于D，取c=0，则ac=bc，故D错误；
对于C，因为c2+1≥1>0，则1c2+1>0，
又a>b，所以ac2+1>bc2+1，故C正确.
故选：C.
2．（2023·天津·一模）设a>0，b>0，则“a>b”是“1a0，由1a0，则a−b>0，即a>b，
因此，若a>0，b>0，则“a>b”是“1a1”是“a+1a>2”的（ ）．
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】A
【分析】判断“a>1”和“a+1a>2”之间的逻辑推理关系，即得答案.
【详解】当a>1时，a+1a−2=a2−2a+1a=(a−1)2a>0，
故a+1a>2，即a>1成立，则a+1a>2成立；
当a=12时，a+1a=12+2>2，但推不出a>1成立，
故“a>1”是“a+1a>2”的充分不必要条件，
故选：A
4．（2024·北京西城·一模）设a=t−1t,b=t+1t,c=t2+t，其中−10，
f'x=3ax2+2bx+c有两个不相等的正实数根x1,x2，且fx在−∞,x1,x2,+∞上单调递增，在x1,x2上单调递减，
所以a>0,x1+x2=−2b3a>0,x1x2=c3a>0，
所以b0，
综上：a>0，b0，d>0.
故选：A
3．（2023·全国·高考真题）已知集合M=−2,−1,0,1,2，N=xx2−x−6≥0，则M∩N=（ ）
A．−2,−1,0,1B．0,1,2C．−2D．2
【答案】C
【分析】方法一：由一元二次不等式的解法求出集合N，即可根据交集的运算解出．
方法二：将集合M中的元素逐个代入不等式验证，即可解出．
【详解】方法一：因为N=xx2−x−6≥0=−∞,−2∪3,+∞，而M=−2,−1,0,1,2，
所以M∩N= −2．
故选：C．
方法二：因为M=−2,−1,0,1,2，将−2,−1,0,1,2代入不等式x2−x−6≥0，只有−2使不等式成立，所以M∩N= −2．
故选：C．
4．（2017·天津·高考真题）设x∈R，则2−x≥0是−1≤x−1≤1 的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】B
【分析】根据充分条件、必要条件的定义结合集合的包含关系可解．
【详解】设p：若2−x≥0，则x≤2，
q：若−1≤x−1≤1，则0≤x≤2；
则q表示的集合是p表示的集合真子集，
即2−x≥0是−1≤x−1≤1必要不充分条件，
故选：B．
5．（天津·高考真题）设集合A=x|4x−1|≥9,x∈R,B=xxx+3≥0,x∈R，则A∩B=（ ）
A．(−3,−2]B．(−3,−2]∪0,52C．(−∞,−3]∪52,+∞D．(−∞,−3)∪52,+∞
【答案】D
【分析】根据含绝对值不等式和分式不等式的解法求出集合A,B，再根据交集的定义即可得出答案.
【详解】因为A=x4x−1≥9,x∈R={xx≥52或x≤−2=−∞,−2∪52,+∞，
B=x|xx+3≥0,x∈R=xx≥0或x0)的解集
{x|xx2}
eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠－\f(b,2a)))))
R
ax2＋bx＋c0)的解集
{x|x1