



第12讲 函数的单调性与最值(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案
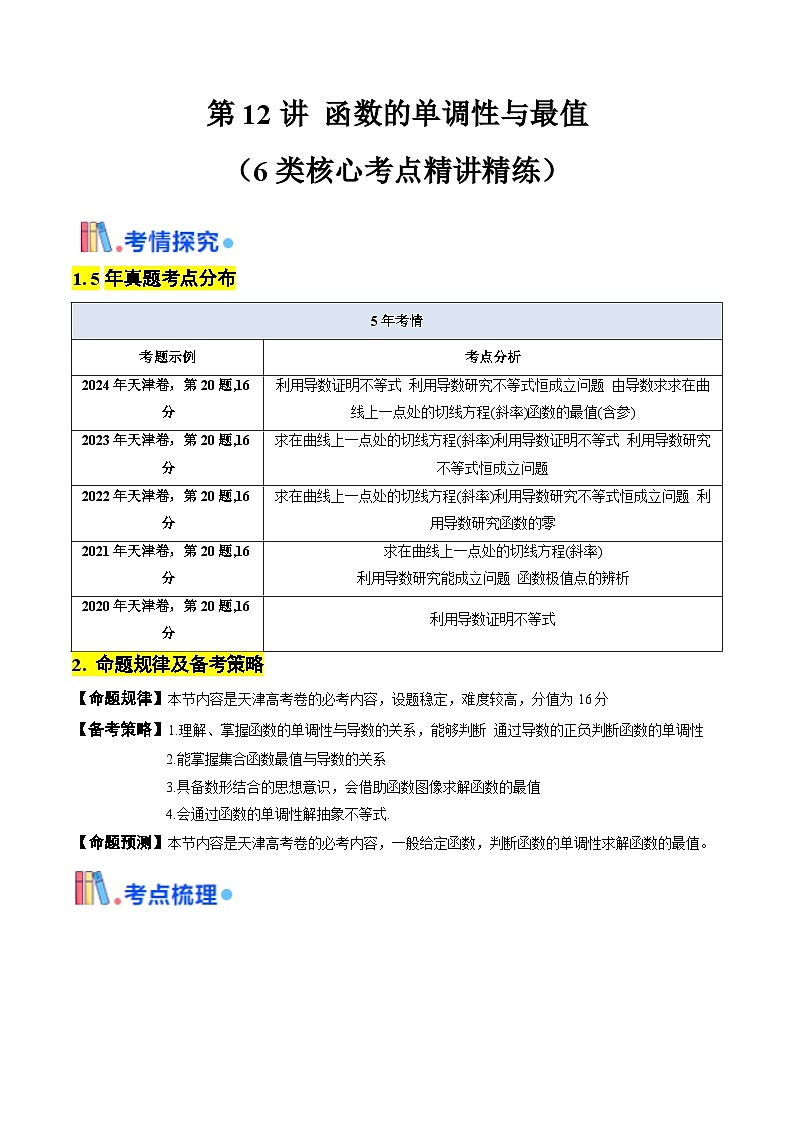
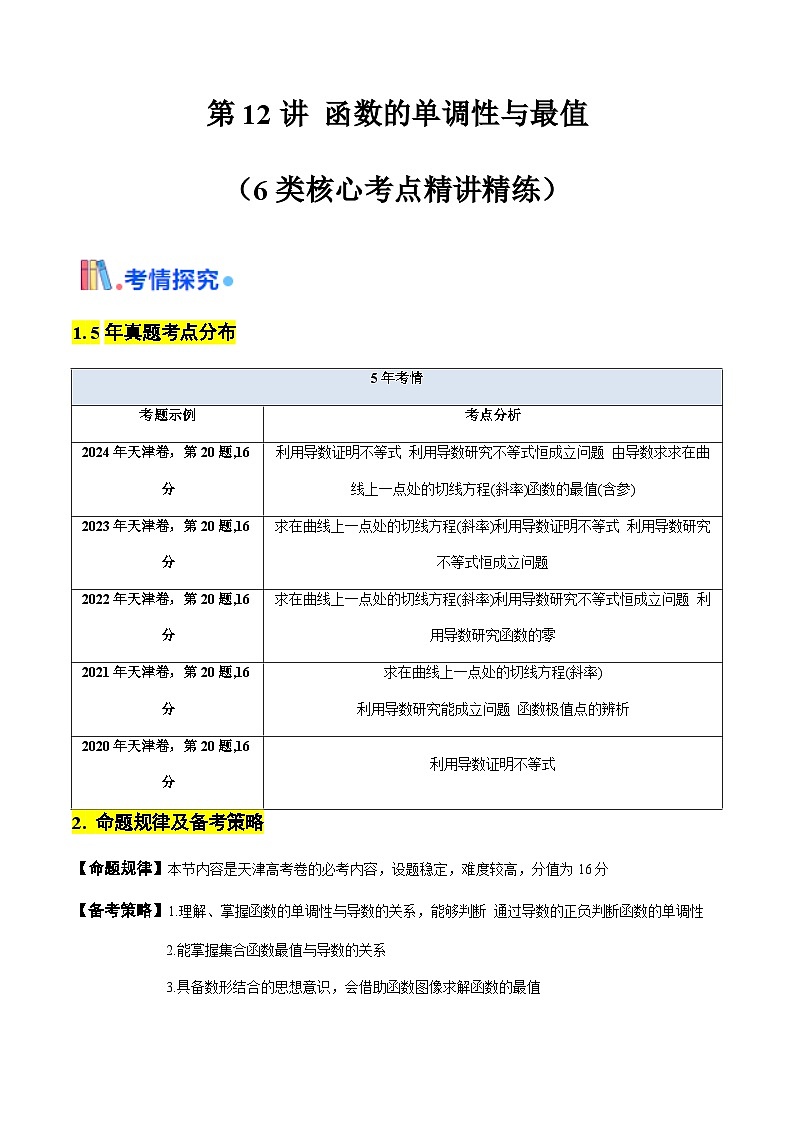
展开1. 5年真题考点分布
2. 命题规律及备考策略
【命题规律】本节内容是天津高考卷的必考内容,设题稳定,难度较高,分值为16分
【备考策略】1.理解、掌握函数的单调性与导数的关系,能够判断 通过导数的正负判断函数的单调性
2.能掌握集合函数最值与导数的关系
3.具备数形结合的思想意识,会借助函数图像求解函数的最值
4.会通过函数的单调性解抽象不等式.
【命题预测】本节内容是天津高考卷的必考内容,一般给定函数,判断函数的单调性求解函数的最值。
知识讲解
知识点一.函数的单调性
1.函数的单调性与导数的关系
2.常用结论
(1)在某区间内f′(x)>0(f′(x)<0)是函数f(x)在此区间上为增(减)函数的充分不必要条件.
(2)可导函数f(x)在(a,b)上是增(减)函数的充要条件是对∀x∈(a,b),都有f′(x)≥0(f′(x)≤0)且f′(x)在(a,b)上的任何子区间内都不恒为零.
知识点二.函数的最值与导数
1.函数f(x)在[a,b]上有最值的条件
如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
2.求y=f(x)在[a,b]上的最大(小)值的步骤
(1)求函数y=f(x)在(a,b)内的极值;
(2)将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
3.常用结论.
(1)若函数f(x)的图象连续不断,则f(x)在[a,b]上一定有最值.
(2)若函数f(x)在[a,b]上是单调函数,则f(x)一定在区间端点处取得最值.
(3)若函数f(x)在区间(a,b)内只有一个极值点,则相应的极值点一定是函数的最值点.
考点一、不含参函数的单调性与单调区间
1.(广东·高考真题)设函数fx=xlnx,则fx的单调递增区间为 .
2.(重庆·高考真题)设函数f(x)=x3+ax2−9x−1(a<0).若曲线y=fx的斜率最小的切线与直线12x+y=6平行,求:
(Ⅰ)a的值;
(Ⅱ)函数y=fx的单调区间.
1.(2005·北京·高考真题)已知函数fx=−x3+3x2+9x+a
(1)求fx的单调减区间;
(2)若fx在区间−2,2上的最大值为20,求它在该区间上的最小值.
2.(2024·黑龙江·模拟预测)已知f(x)=ax+bcsx在点π2,fπ2处的切线方程为x+2y−π=0.
(1)求a,b的值;
(2)求fx在区间[0,π]的单调区间和极值.
3.(2025·甘肃张掖·模拟预测)已知函数fx=ex−alnx+1的图象在点0,f0处的切线过点2,1.
(1)求实数a的值;
(2)求fx的单调区间和极值.
考点二、含参函数的单调性与单调区间
1.(·北京·高考真题)已知函数f(x)=2x−b(x−1)2,求导函数f'(x),并确定f(x)的单调区间.
2.(全国·高考真题) 已知a∈R,求函数f(x)=x2eax的单调区间.
1.(2025高三·全国·专题练习)已知函数f(x)=ax−1x−(a+1)lnx(a≠0),讨论函数f(x)的单调性.
2.(23-24高三下·北京·阶段练习)已知函数fx=2ax−lnx+1x,a≠0.
(1)若a=1,求函数fx的极值;
(2)试讨论函数fx的单调性.
3.(北京·高考真题)已知函数f(x)=x3+ax2+3bx+c(b≠0),且g(x)=f(x)−2是奇函数.
(Ⅰ)求a,c的值;
(Ⅱ)求函数f(x)的单调区间.
考点三、已知函数的单调性求参数
1.(2023·全国·高考真题)已知函数fx=aex−lnx在区间1,2上单调递增,则a的最小值为( ).
A.e2B.eC.e−1D.e−2
2.(2023·全国·高考真题)设a∈0,1,若函数fx=ax+1+ax在0,+∞上单调递增,则a的取值范围是 .
1.(2019·北京·高考真题)设函数f(x)=ex+ae−x(a为常数).若f(x)为奇函数,则a= ;若f(x)是R上的增函数,则a的取值范围是 .
2.(2016·全国·高考真题)若函数fx=x−13sin2x+asinx在R上单调递增,则a的取值范围是
A.−1,1B.−1,13C.−13,13D.−1,−13
3.(上海·高考真题)已知函数f(x)=x2+ax(x≠0,常数a∈R).
(1)讨论函数fx的奇偶性,并说明理由;
(2)若函数fx在[2,+∞)上为增函数,求a的取值范围.
4.(23-24高三上·海南海口·阶段练习)已知函数fx=2−xex−ax在0,5上为减函数,则a的取值范围是( )
A.−∞,5eB.5e,+∞C.1,+∞D.1,+∞
5.(2023·宁夏银川·三模)若函数f(x)=x22−lnx在区间(m,m+13)上不单调,则实数m的取值范围为( )
A.0
考点四、已知函数存在单调性求参数
1.(23-24高三上·福建泉州·阶段练习)若函数ℎx=lnx−12ax2−2x在[1,4]上存在单调递增区间,则实数a的取值范围为( )
A.−1,+∞B.−1,+∞C.−∞,−716D.−∞,−716
2.(2024·内蒙古呼和浩特·一模)在区间(0,π)上,函数y=a−csxx存在单调递增区间,则实数a的取值范围是( )
A.(−∞,1)B.(−∞,π2]
C.(−∞,π2)D.(−∞,1]
1.(22-23高三上·陕西·期中)若函数f(x)=x3+bx2+3x在13,2上存在单调递增区间,则b的取值范围是( )
A.−5,+∞B.−3,+∞C.−∞,−5D.−∞,−3
2.(21-22高三上·江苏苏州·期中)若函数fx=lnx+ax2−2在区间12,2内存在单调递增区间,则实数a的取值范围是( )
A.−2,+∞B.−18,+∞C.−2,−18D.−2,+∞
3.(2024·全国·模拟预测)已知函数fx=14x4−23x3+a2x2−xlnx在1e,2上存在单调递减区间,则实数a的取值范围为( )
A.−∞,2e−1e2B.−∞,2
C.−∞,2e−1e2D.−∞,2
4.(23-24高三上·陕西汉中·期末)若函数fx=lnx+ax2−2在区间14,1内存在单调递增区间,则实数a的取值范围是 .
5.(24-25高三·上海·随堂练习)设函数y=fx,其中fx=ax−lnxa>0,
(1)求f'x;
(2)若y=fx在[1,+∞)是严格增函数,求实数a的取值范围;
(3)若y=fx在[2,4]上存在单调递减区间,求实数a的取值范围.
考点五、求已知函数的最值
1.(2021·全国·高考真题)函数f(x)=|2x−1|−2lnx的最小值为 .
2.(2018·全国·高考真题)已知函数fx=2sinx+sin2x,则fx的最小值是 .
1.(2021·北京·高考真题)已知函数fx=3−2xx2+a.
(1)若a=0,求曲线y=fx在点1,f1处的切线方程;
(2)若fx在x=−1处取得极值,求fx的单调区间,以及其最大值与最小值.
2.(2020·北京·高考真题)已知函数f(x)=12−x2.
(Ⅰ)求曲线y=f(x)的斜率等于−2的切线方程;
(Ⅱ)设曲线y=f(x)在点(t,f(t))处的切线与坐标轴围成的三角形的面积为S(t),求S(t)的最小值.
3.(2017·北京·高考真题)已知函数f(x)=excsx−x.
(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)求函数f(x)在区间[0,π2]上的最大值和最小值.
4.(24-25高三·上海·随堂练习)函数y=32x2+a+4x−2lnx在区间(1,2)上存在最值,则实数a的取值范围为( ).
A.(5,9)B.(-5,9)C.(−9,5)D.(−9,−5)
5.(24-25高三·上海·随堂练习)函数y=x3−3x−a在区间0,3上的最大值、最小值分别为M,N,则M−N=( ).
A.14B.16C.18D.20
考点六、利用单调性解抽象不等式
1.(2007·陕西·高考真题)fx是定义在(0,+∞)上的非负可导函数,且满足xf'x+fx≤0.对任意正数a,b,若a
C.afa≤fbD.bfb≤fa
2.(2004·湖南·高考真题)设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f'(x)g(x)+f(x)g'(x)>0.且g(−3)=0,则不等式f(x)g(x)<0的解集是( )
A.(−3,0)∪(3,+∞)B.(−3,0)∪(0,3)
C.(−∞,−3)∪(3,+∞)D.(−∞,−3)∪(0,3)
1.(江西·高考真题)对于R上可导的任意函数fx,若满足x−1f'x≥0则必有
A.f0+f2<2f1B.f0+f2≤2f1
C.f0+f2≥2f1D.f0+f2>2f1
2.(2024·山东潍坊·三模)已知函数fx的导函数为f'x,且f1=e,当x>0时,f'x<1x+ex,则不等式fx−lnxex>1的解集为( )
A.0,1B.0,+∞C.1,+∞D.0,1∪1,+∞
3.(2024·吉林·二模)已知函数fx的定义域为−∞,0,其导函数f'x满足xf'x−2fx>0,则不等式fx+2024−x+20242f−1<0的解集为( )
A.−2025,−2024B.−2024,0
C.−∞,−2024D.−∞,−2025
4.(2024·宁夏银川·三模)已知定义在R上的奇函数f(x)的图象是一条连续不断的曲线,f'(x)是f(x)的导函数,当x>0时,3f(x)+xf'(x)>0,且f(2)=2,则不等式(x+1)3f(x+1)>16的解集为( )
A.(1,+∞)B.(−∞,−2)∪(2,+∞)
C.(−∞,1)D.(−∞,−3)∪(1,+∞)
5.(2024·江西南昌·三模)已知函数f(x)的定义域为R,且f2=−1,对任意x∈R,f(x)+xf'(x)<0,则不等式x+1fx+1>−2的解集是( )
A.−∞,1B.−∞,2C.1,+∞D.2,+∞
1.(2020高三·山东·专题练习)若函数y=x3+x2+mx+1是R上的单调函数,则实数m的取值范围是( ).
A.−∞,13B.13,+∞C.−∞,13D.13,+∞
2.(23-24高三上·天津东丽·期中)函数f(x)=12x2+csx,则不等式f(lnx)>f(1)的解集为( )
A.(0,e)B.(e,+∞)C.1e,eD.0,1e∪(e,+∞)
3.(22-23高三上·上海浦东新·期中)已知fx=2x2−ax+lnx在区间1,+∞上单调递增,则实数a的取值范围是 .
4.(23-24高三上·天津河东·阶段练习)若函数fx=x3−3ax2−2x+5在0,1内单调递减,则实数a的取值范围是
5.(20-21高三下·天津静海·阶段练习)已知函数f(x)=12x2−2alnx+(a−2)x.
(1)当a=−1时,求函数f(x)的单调区间;
(2)是否存在实数a,使函数g(x)=f(x)−ax在(0,+∞)上单调递增?若存在,求出a的取值范围;若不存在,请说明理由.
6.(20-21高三上·天津·期中)设函数fx=x3+mx+1,曲线y=fx在点1,f1处的切线与x轴平行.
(1)求实数m;
(2)求fx的单调区间.
7.(23-24高三上·天津河东·阶段练习)设函数fx=lnx+mx.
(1)当m=2时,求fx在1,f1处的切线方程;
(2)讨论fx的单调性;
(3)若fx≥3−x恒成立,求m的取值范围.
1.(23-24高三下·天津·阶段练习)已知函数fx=ax−sinxcs3x,x∈0,π2,
(1)当a=0时,求fx在点π4,fπ4处的切线方程;
(2)当a=8时,讨论函数fx的单调性;
(3)若fx
(1)求fx的单调区间;
(2)证明:fx
3.(23-24高三上·天津·期末)已知函数fx=lnx+1,gx=ex.
(1)求曲线y=fx在点0,f0处的切线方程;
(2)证明:gx≥fx+1;
(3)当x≥0时,ax⋅fx≤gx−x−1恒成立,求实数a的取值范围.
4.(23-24高三上·天津河北·期末)已知函数fx=4ax2+x−1ex.
(1)当a=1时,求曲线y=fx在点0,f0处的切线方程;
(2)当a>0时,求函数y=fx的单调区间;
(3)在(2)的条件下,当x∈1,3时,12≤fx≤1,求实数a的取值范围.
5.(23-24高三上·广东深圳·阶段练习)已知函数f(x)=(x−1)ex+ax2,a∈R.
(1)讨论f(x)的单调性;
(2)当a<−1时,若f(x)的极小值点为x0,证明:f(x)存在唯一的零点x1,且x1−x0≥ln2.
6.(23-24高三上·天津静海·阶段练习)已知函数fx=ex+a−1x−1,其中a∈R.
(1)当a=3时,求曲线y=fx在点0,f0处的切线方程;
(2)讨论函数fx的单调性;
(3)当a>1时,证明:fx>xlnx−acsx.
7.(23-24高三上·天津·期中)已知函数fx=lnx+a+1x+1,a∈R,gx=xex.
(1)若曲线fx在点1,f1处的切线的斜率为3,求a的值;
(2)当x≥−2 时,函数y=gx−m+2有两个不同零点,求m的取值范围;
(3)若∀x∈0,+∞,不等式g'x−fx≥ex恒成立,求实数a的取值范围.
1.(重庆·高考真题)设函数fx=x3−3ax2+3bx的图象与直线12x+y−1=0相切于点1,−11.
(1)求a,b的值;
(2)求函数fx的单调区间.
2.(海南·高考真题)设函数fx=ln2x+3+x2
(1)讨论fx的单调性;
(2)求fx在区间−34,14的最大值和最小值.
3.(北京·高考真题)已知函数f(x)=In(1+x)-x+k2x2(k≥0).
(Ⅰ)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)的单调区间.
4.(2023·全国·高考真题)已知函数fx=1x+aln1+x.
(1)当a=−1时,求曲线y=fx在点1,f1处的切线方程.
(2)若函数fx在0,+∞单调递增,求a的取值范围.
5.(天津·高考真题)若函数fx=lgax3−ax(a>0且a≠1)在区间−12,0内单调递增,则a的取值范围是( )
A.14,1B.34,1C.94,+∞D.1,94
6.(2022·全国·高考真题)函数fx=csx+x+1sinx+1在区间0,2π的最小值、最大值分别为( )
A.−π2,π2B.−3π2,π2C.−π2,π2+2D.−3π2,π2+2
7.(2022·全国·高考真题)当x=1时,函数f(x)=alnx+bx取得最大值−2,则f'(2)=( )
A.−1B.−12C.12D.1
5年考情
考题示例
考点分析
2024年天津卷,第20题,16分
利用导数证明不等式 利用导数研究不等式恒成立问题 由导数求求在曲线上一点处的切线方程(斜率)函数的最值(含参)
2023年天津卷,第20题,16分
求在曲线上一点处的切线方程(斜率)利用导数证明不等式 利用导数研究不等式恒成立问题
2022年天津卷,第20题,16分
求在曲线上一点处的切线方程(斜率)利用导数研究不等式恒成立问题 利用导数研究函数的零
2021年天津卷,第20题,16分
求在曲线上一点处的切线方程(斜率)
利用导数研究能成立问题 函数极值点的辨析
2020年天津卷,第20题,16分
利用导数证明不等式
条件
结论
函数y=f(x)在
区间(a,b)上可导
f′(x)>0
f(x)在(a,b)内单调递增
f′(x)<0
f(x)在(a,b)内单调递减
f′(x)=0
f(x)在(a,b)内是常数函数
第24讲 数列的概念(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案: 这是一份第24讲 数列的概念(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案,文件包含第24讲数列的概念教师版备战2025年高考数学一轮复习考点帮天津专用docx、第24讲数列的概念学生版备战2025年高考数学一轮复习考点帮天津专用docx等2份学案配套教学资源,其中学案共48页, 欢迎下载使用。
第23讲 复数(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案: 这是一份第23讲 复数(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案,文件包含第23讲复数教师版备战2025年高考数学一轮复习考点帮天津专用docx、第23讲复数学生版备战2025年高考数学一轮复习考点帮天津专用docx等2份学案配套教学资源,其中学案共35页, 欢迎下载使用。
第13讲函数的极值(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案: 这是一份第13讲函数的极值(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案,文件包含第13讲函数的极值教师版备战2025年高考数学一轮复习考点帮天津专用docx、第13讲函数的极值学生版备战2025年高考数学一轮复习考点帮天津专用docx等2份学案配套教学资源,其中学案共54页, 欢迎下载使用。












