2024-2025学年北师大版九年级上册数学期中测试卷（第一章-第三章）

这是一份2024-2025学年北师大版九年级上册数学期中测试卷（第一章-第三章），共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题(共10题；共30分)
1．（3分）在一个不透明的袋子里装有红球，黄球共60个，这些球除颜色外其他都相同.小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能是（ ）
A．9B．15C．18D．24
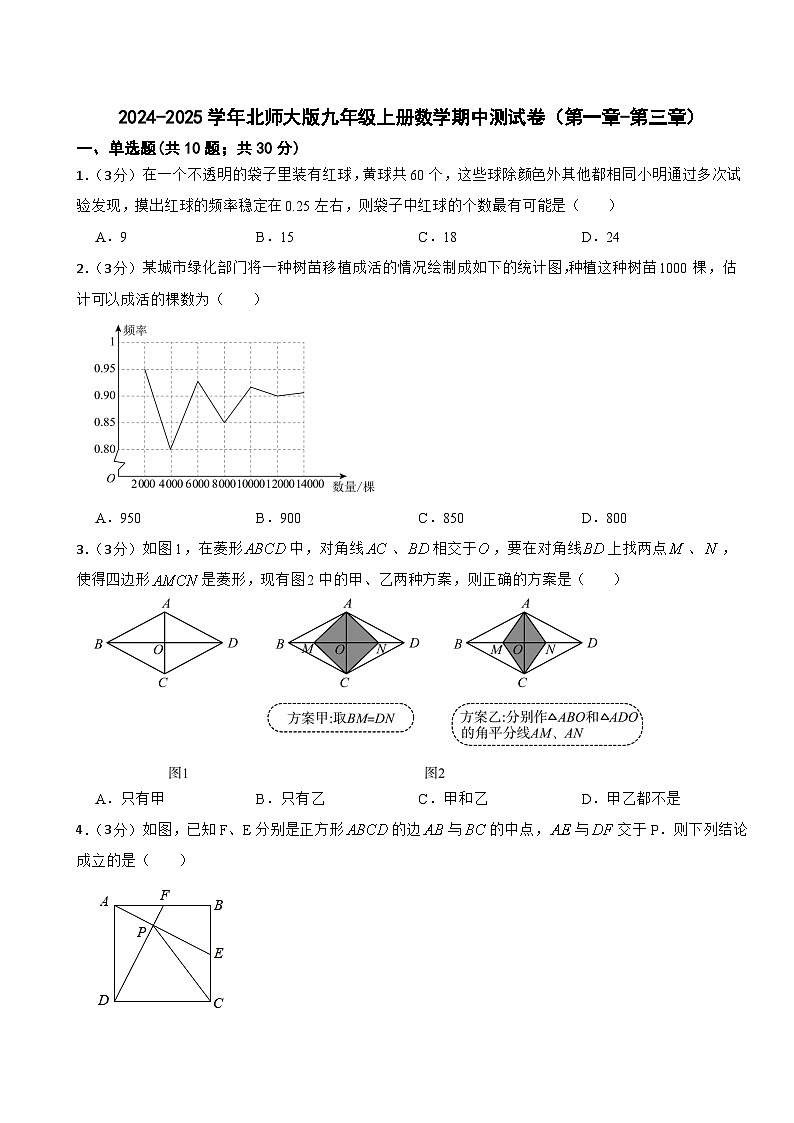
2．（3分）某城市绿化部门将一种树苗移植成活的情况绘制成如下的统计图，种植这种树苗1000棵，估计可以成活的棵数为（ ）
A．950B．900C．850D．800
3．（3分）如图1，在菱形中，对角线、相交于，要在对角线上找两点、，使得四边形是菱形，现有图2中的甲、乙两种方案，则正确的方案是（ ）
A．只有甲B．只有乙C．甲和乙D．甲乙都不是
4．（3分）如图，已知F、E分别是正方形的边与的中点，与交于P．则下列结论成立的是（ ）
A．B．
C．D．
5．（3分）如图，已知，从下列四个条件中选两个作为补充条件，使成为正方形．
①；②；③；④．
下列四种选法错误的是（ ）
A．①②．B．①③．C．②③．D．①④．
6．（3分）如图，已知线段AB，按下列步骤作图：分别以A、B为圆心，大于AB长为半径画弧，两弧相交于点M、N，作直线MN，交AB于点O，分别连接MA、MB、NA、NB，如果四边形MANB是正方形，需要添加的条件是（ ）
A．AO＝MOB．MA∥NBC．MA＝NBD．AB平分∠MAN
7．（3分）如图，在中，点分别在边，，上，且，．下列四个判断中，不正确的是（ ）
A．四边形是平行四边形
B．如果，那么四边形是矩形
C．如果平分平分∠BAC，那么四边形 AEDF 是菱形
D．如果AD⊥BC 且 AB＝AC，那么四边形 AEDF 是正方形
8．（3分）如图所示，正方形ABCD的边长为2，E为与点D不重合的动点，以DE为一边作正方形DEFG.设DE=d1，点F，G与点C的距离分别为d2，d3，则d1+d2+d3的最小值为（ ）
A．B．2C．2D．4
9．（3分）如图，在正方形中，为边上一点（点不与点，重合），于，并交于点，交延长线于点．给出下面三个结论：①；②；③．上述结论中，所有正确结论的序号是（ ）
A．仅有②B．仅有③C．②③D．①②③
10．（3分）如图，扇形OAB的半径OA＝9，圆心角∠AOB＝90°，C是AB上不同于A，B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连接DE，点H在线段DE上，且EH＝ DE.则△CEH面积的最大值为（ ）
A．B．C．D．
二、填空题(共6题；共18分)
11．（3分）将一张长方形纸片按如图所示方式折叠，、为折痕，点B、D折叠后的对应点分别为、，若，则的度数为 ．
12．（3分）某校组织“歌唱祖国”合唱比赛，七年一班准备从《我和我的祖国》、《国家》、《龙的传人》三首歌曲中选择两首进行排练，那么该班恰好选中《国家》、《龙的传人》这两首歌的概率是 ．
13．（3分）如图，分别以菱形的顶点为圆心，以大于长为半径画弧，两弧分别相交于点，直线恰好经过菱形的顶点，则对角线与边的夹角的度数为 度．
14．（3分）如图，在矩形ABCD中，对角线AC，BD相交于点O，若OA＝2，则BD的长为 ．
15．（3分）如图所示是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A，B，C，D的面积分别为2，5，1，2．则最大的正方形E的面积是
16．（3分）如图，在矩形 中， ， ，点P为 边上一点，将 沿 翻折，点A落在点 处，当点 在矩形的对角线上时， 的长度为 ．
三、解答题(共7题；共52分)
17．（6分）为了弘扬中华优秀传统文化，丰富校园文化生活，某校积极筹备校园艺术节，九年级一班、二班准备在“民歌串烧”“民族舞蹈”“民乐演奏”中分别选择一个节目进行表演．学校把这三个节目名分别写在三张完全相同的不透明的卡片的正面上，然后将这三张卡片背面朝上洗匀后放在桌面上．
（1）（2分）九年级一班随机抽取一张卡片，则抽中“民族舞蹈”的概率是__________；
（2）（4分）—班同学先从中随机抽取一张卡片，记录下卡片上的节目后放回，二班同学再随机抽取一张卡片，记录下卡片上的节目．请用列表法或画树状图法求出一班、二班同学表演不同节目的概率．
18．（7分）如图，在中，，平分，交于点，过点作交于点．
（1）（3分）求证：四边形是菱形；
（2）（4分）若菱形的周长为，，求的大小．
19．（7分）如图所示，在矩形ABCD中，AB＝8，AD＝10，将矩形沿直线AE折叠，顶点D恰好落在BC边上的点F处，求CE的长．
20．（7分）如图所示，有张除了正面图案不同，其余都相同的图片．
以上四张图片所示的立体图形中，主视图是矩形的有________；（填字母序号）
将这四张图片背面朝上混匀，从中随机抽出一张后放回，混匀后再随机抽出一张．求两次抽出的图片所示的立体图形中，主视图都是矩形的概率．
21．（8分）定义：对角线垂直的凸四边形叫做“准筝形”．如图1，四边形中，，则四边形是“准筝形”．
（1）（2分）“一组邻边相等的准筝形是菱形”是______命题；（填“真”或“假”）
（2）（3分）如图1，在准筝形中，，，，且满足，，求的长．
（3）（3分）如图2，在准筝形中，与交于点O，点P在线段上，且，，在上存在移动的线段，E在F的左侧，且，使四边形的周长最小，求此时的长度．
22．（8分）【问题提出】
（1）如图1，在菱形中，，其中分别是边上的中点，则的周长为 ；
【问题探究】
（2）如图2，在四边形中，，点在边上，点在边上，且，则周长的最小值为 ；
【问题解决】
（3）如图3，规划部门准备绿化一块四边形空地，计划在边，上分别取点，，利用小路，将这块四边形空地分开，在四边形空地内种植郁金香，其他区域种植草坪，为了方便市民游览，决定取的中点，沿着修建观赏长廊．经测量，，，，，为节约建设成本，修建长廊长度之和应该最短．请你帮助规划部门确定是否有最小值．若存在，请求出的最小值；若不存在，请说明理由．
23．（9分）如图1，已知O是坐标原点，点A的坐标是(5，0)，B是y轴正半轴上一动点，以OB，OA为边作矩形OBCA，点E，H分别在边BC和OA上，将△BOE沿着OE对折，使点B落在OC上的点F处，将△ACH沿着CH对折，使点A落在OC上的点G处.
（1）（3分）求证：四边形OECH是平行四边形.
（2）（3分）如图2，当点F，G重合时，求点B的坐标.判断四边形OECH的形状，并说明理由.
（3）（3分）当点F，G将对角线OC三等分时，求点B的坐标.
答案解析部分
1．【答案】B
2．【答案】B
3．【答案】C
4．【答案】C
5．【答案】A
6．【答案】A
7．【答案】D
8．【答案】C
9．【答案】C
10．【答案】A
11．【答案】
12．【答案】
13．【答案】30
14．【答案】4
15．【答案】10
16．【答案】 或
17．【答案】（1）
（2）
18．【答案】（1）证明：四边形为平行四边形，
，即 ，
，
∴四边形为平行四边形，
平分，
，
，
，
，
，
∴四边形是菱形；
（2）解：连接交于点；则于点，
，，
，
∵菱形的周长为，
，
在中，
，
由勾股定理可得：，
．
19．【答案】解：∵四边形ABCD是矩形，
∴AB＝DC＝8，AD＝BC＝10，
∵矩形沿直线AE折叠，顶点D恰好落在BC边上的点F处，
∴AD＝AF＝10，DE＝FE，
∴在Rt△ABF中，BF＝＝＝6，
∴FC＝BC-BF＝10-6＝4，
设DE＝FE＝x，则CE＝DC-x＝8-x，
∴在Rt△FCE中，FC2+CE2＝FE2，
∴42+(8-x)2＝x2，解得x＝5，
∴CE＝8-x＝8-5＝3
20．【答案】（1）B、D；（2）.
21．【答案】（1）假
（2）；
（3）．
22．【答案】（1）（2）（3）存在，
23．【答案】（1）证明：∵四边形OBCA为矩形，
∴OB//CA，BC//OA，
∴∠BOC=∠OCA，
由折叠的性质可得：∠BOC=2∠EOC，∠OCA=2∠OCH，
∴∠EOC=∠OCH，
∴OE//CH，
又∵BC//OA，
∴四边形OECH是平行四边形；
（2）解：四边形OECH是菱形．理由如下：
由折叠的性质可得∠EFO=∠EBO=90°，∠CFH=∠CAF=90°，
∵点F，G重合，
∴EH⊥OC，
又∵四边形OECH是平行四边形，
∴平行四边形OECH是菱形，
∴EO=EC，
∴∠EOC=∠ECO，
又∵∠EOC=∠BOE，
∴∠EOB=∠EOC=∠ECO=30°，
点A的坐标是（5，0），
∴OA=5，
由直角三角形的性质可得：OB=
∴点B的坐标是（0，）；
（3）解：当点F在点O，G之间时，如图3，
由折叠性质得：OF=OB，CG=CA，
而OB=CA，
∴OF=CG，
∵点F，G将对角线OC三等分，
∴AC=OF=FG=GC，
设AC=m，则OC=3m，
在Rt△OAC中，OA=5，
由勾股定理得：AC2+OA2=OC2，
即：m2+52=（3m）2，解得m=，
∴OB=AC=，
∴点B的坐标是（0，）；
当点G在O，F之间时，如图4，
同理可得OF=CG=AC，
设OG=n，则AC=GC=2n，
在Rt△OAC中，OA=5，
由勾股定理得：AC2+OA2=OC2，
即：（2n）2+52=（3n）2，解得n=，
∴AC=OB=2，
∴点B的坐标是（0，2）．
故B的坐标是（0，）或（0，2）．