江苏省苏州市2024-2025学年九年级上学期期中数学摸底调研卷

这是一份江苏省苏州市2024-2025学年九年级上学期期中数学摸底调研卷，共19页。试卷主要包含了单选题，解答题，填空题等内容，欢迎下载使用。
（总分：130分；考试时长：120分钟）
第Ⅰ卷（选择题）
一、单选题（共8小题，每小题3分，满分24分）
1．下列一组数据5，3，4，5，3，3的中位数是（ ）
A．3B．C．4D．
2．二次函数的图象与轴的交点坐标为（ ）
A．B．C．D．
3．下列哪一个函数，其图形与轴有两个交点（ ）
A．B．
C．D．
4．某农机厂四月份生产零件40万个，第二季度共生产零件162万个．设该厂五、六月份平均每月的增长率为x，那么x满足的方程是（ ）
A．40（1+x）2=162
B．40+40（1+x）+40（1+x）2=162
C．40（1+2x）=162
D．40+40（1+x）+40（1+2x）=162
5．如图①，“东方之门”通过简单的几何曲线处理，将传统文化与现代建筑融为一体，最大程度地传承了苏州的历史文化．如图②，“门”的内侧曲线呈抛物线形，已知其底部宽度为80米，高度为200米．则离地面150米处的水平宽度（即CD的长）为（ ）
A．40米B．30米C．25米D．20米
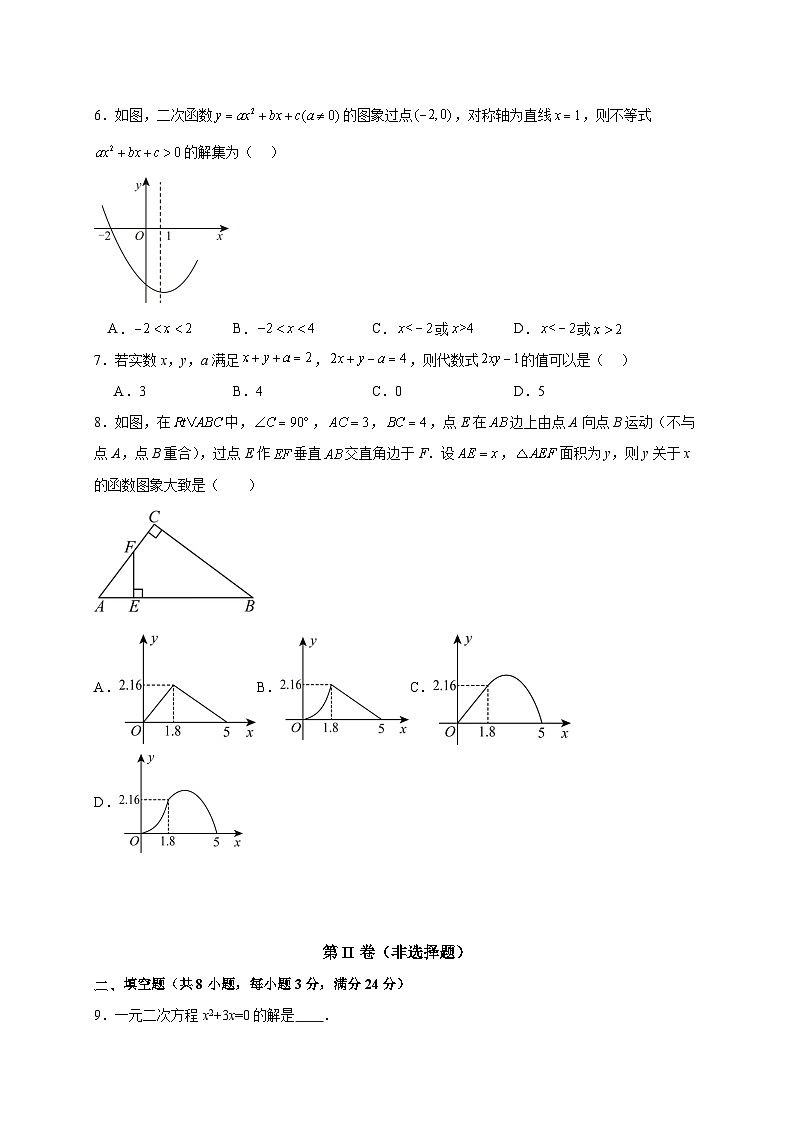
6．如图，二次函数的图象过点，对称轴为直线，则不等式的解集为（ ）
A．B．C．或 D．或
7．若实数x，y，a满足，，则代数式的值可以是（ ）
A．3B．4C．0 D．5
8．如图，在中，，，，点E在边上由点A向点B运动（不与点A，点B重合），过点E作垂直交直角边于F．设，面积为y，则y关于x的函数图象大致是（ ）
A．B．C．D．
第II卷（非选择题）
填空题（共8小题，每小题3分，满分24分）
9．一元二次方程x2+3x=0的解是 ．
10．已知抛物线与x轴交于A、B两点（点A在点B左侧），则线段的长为 ．
11．对于实数，，新定义一种运算“※”：※．若※，则的值为 ．
12．如图，物体从点A抛出，物体的高度y（单位：）与飞行时间t（单位：）近似满足函数关系式．在飞行过程中，若物体在某一个高度时总对应两个不同的时间，则t的取值范围是 ．

13．已知实数m，n满足，，且，若，则代数式的最小值是 ．
14．如果关于x的一元二次方程ax2+bx+c＝0有两个实数根，其中一个根为另一个根的，则称这样的方程为“半根方程”．例如方程x2﹣6x+8＝0的根为的x1＝2，x2＝4，则x1＝x2，则称方程x2﹣6x+8＝0为“半根方程”．若方程ax2+bx+c＝0是“半根方程”，且点P（a，b）是函数y＝x图象上的一动点，则的值为 ．
15．已知实数m，n满足m﹣n2＝3，则代数式m2+2n2﹣6m﹣2的最小值等于 ．
16．二次函数y＝2x2的图象如图所示，坐标原点O，点B1，B2，B3在y轴的正半轴上，点A1，A2，A3在二次函数y＝2x2位于第一象限的图象上，若△A1OB1，△A2B1B2，△A3B2B3都为等腰直角三角形，且点A1，A2，A3均为直角顶点，则点A3的坐标是 ．
三、解答题
17．解下列方程：
（1）x2﹣4x＝1 （2）x（2x﹣1）＝3（2x﹣1）
18．先化简，再求值：，其中x满足x2+3x﹣4＝0．
19．已知关于x的一元二次方程2x2﹣（a＋1）x＋a﹣1＝0（a为常数）
（1）当a＝2时，求出该一元二次方程实数根；
（2）若x1，x2是这个一元二次方程两根，且x1，x2是以为斜边的直角三角形两直角边，求a的值．
20．一个不透明的袋子中装有四个小球，球面上分别标有数字-1，0，1，2四个数字．这些小球除了数字不同外，其他都完全相同，袋内小球充分搅匀．
（1）随机地从袋中摸出一个小球，则摸出标有数字2的小球的概率为 ；
（2）小强设计了如下游戏规则：先从袋中随机摸出一个小球（不放回），然后再从余下的三个小球中随机摸出一个小球．把2次摸到的小球数字相加，和为奇数，甲获胜；和为偶数，乙获胜．小强设计的游戏规则公平吗？为什么？（请用画树状图或列表说明理由）
21．2020年东京奥运会于2021年7月23日至8月8日举行，跳水比赛是大家最喜爱观看的项目之一，其计分规则如下：
a．每次试跳的动作，按照其完成难度的不同对应一个难度系数H；
b．每次试跳都有7名裁判进行打分（0～10分，分数为0.5的整数倍），在7个得分中去掉2个最高分和2个最低分，剩下3个得分的平均值为这次试跳的完成分p；
c．运动员该次试跳的得分A＝难度系数H×完成分p×3
在比赛中，某运动员一次试跳后的打分表为：
（1）7名裁判打分的众数是 ；中位数是 ．
该运动员本次试跳的得分是多少？
22．如图，二次函数的图象与x轴相交于A（﹣3，0）、B（1，0）两点，与y轴相交于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．
(1)求D点坐标；
(2)求二次函数的解析式；
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围．
23．某牧场准备利用现成的一堵“7”字型的墙面（如图中粗线表示墙面，已知，米，米）和总长为36米的篱笆围建一个“日”形的饲养场（细线表示篱笆，饲养场中间也是用篱笆隔开），如图，点可能在线段上，也可能在线段的延长线上．
（1）当点在线段上时，
①设的长为米，则______米（用含的代数式表示）；
②若要求所围成的饲养场的面积为66平方米，求饲养场的宽；
饲养场的宽为多少米时，饲养场的面积最大？最大面积为多少平方米
24 对于实数a，b，新定义一种运算“※”：a※，例如：∵4＞1，∴4※1＝4×1﹣12＝3
（1）计算：2※（﹣1）＝ ；（﹣1）※2＝ ；
（2）若x1和x2是方程x2﹣5x﹣6＝0的两个根且x1＜x2，求x1※x2的值；
（3）若x※2与3※x的值相等，求x的值
25．某服装店以每件元的价格购进一种服装，由试销知，每天的销售量（件）与每件的销售价（元）之间的函数关系为：．
(1)若服装店一天销售这种服装的毛利润为元，求这种服装每件销售价是多少元?（毛利润=销售价-进货价）
(2)每件服装销售价多少元才能使每天的毛利润最大?最大毛利润是多少?
(3)销售一段时间以后，服装店决定从每天的毛利润中捐出元给慈善机构，若物价部门规定该产品捐款后每天剩余毛利润不能超过元，为了保证捐款后每天剩余毛利润不低于元，请直接写出这种服装每件销售价的范围_______；
26．如图，在平面直角坐标系内，抛物线y＝ax2＋bx﹣4（a≠0）与x轴交于点A，点B，与y轴交于点C，且OB＝2OA．过点A的直线y＝x＋2与抛物线交于点E．点P为第四象限内抛物线上的一个动点，过点P作PH⊥AE于点H．
（1）抛物线的表达式中，a＝ ，b＝ ；
（2）在点P的运动过程中，若PH取得最大值，求这个最大值和点P的坐标；
（3）在（2）的条件下，在x轴上求点Q，使以A，P，Q为顶点的三角形与△ABE相似．
如图（1），抛物线y＝a（x+2）（x－8）（a＜0）的图像与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，连接AC、BC，若△ABC的面积为20．
（1）求a的值，并判断△ABC是什么特殊三角形，说明理由；
（2）如图（2）将△ABC沿x轴翻折，点C的对称点是点D，若点P是抛物线在第一象限图像上的一个动点，设点P的横坐标为m，连接AP、DP，求当m为何值时，△ADP的面积最大；
（3）若点Q是上述抛物线上一点，且满足∠ABQ=2∠ABC，求满足条件的点Q的坐标．
2024-2025年九年级上学期期中摸底答案
数学学科
参考答案：
8．D
【详解】解：过点作于点，
，
，
，
，
当，
，
，
，
，即，
，
，开口向上的一段抛物线；
当，
同理可证，
，即，
，
，开口向下的一段抛物线；
综上，符合题意的函数关系的图象是D；
故选：D．
二、填空题
-3 10．4 11． 12．且
13. 3 14.． 15．﹣11． 16．（，）．
13．3
【详解】解：∵，，
∴，
∴
，
∵实数m，n满足，，且，
∴m、n可看作关于x的一元二次方程的两根，
∴，
∴，
∵，
∴当时，的值随x的增大而增大，
∵，
∴当时，有最小值，最小值为．
故答案为：3．
14．．
∵点P（a，b）是函数y=x图象上的一动点，
∴b=a，
∴方程化为ax2+ax+c=0，
∴由韦达定理得：．
∴．
故答案为：．
15．﹣11．
【详解】∵m﹣n2＝3，
∴n2＝m﹣3，m≥3，
∴m2+2n2﹣6m﹣2
＝m2+2m﹣6﹣6m﹣2
＝m2﹣4m﹣8
＝（m﹣2）2﹣12，
∵（m﹣2）2≥1，
∴（m﹣2）2﹣12≥﹣11，
即代数式m2+2n2﹣6m﹣2的最小值等于﹣11．
故答案为﹣11．
16．（，）．
【详解】分别过A1，A2，A3作y轴的垂线，垂足分别为A、B、C，
设OB1＝a，B1B2＝b，B2B3＝c，则AA1＝a，BA2＝b，CA3＝c，
在等腰直角△OB1A1中，A1（a，a），代入y＝2x2中，得a＝2（a）2，解得a＝1，
∴A1（，），
在等腰直角△B1A2B2中，A2（b，1+b），代入y＝2x2中，得1+b＝2•（b）2，解得b＝2，
∴A2（1，2），
在等腰直角△B2A3B3中，A3（c，3+），代入y＝2x2中，得3+c＝2•（c）2，解得c＝3，
∴A3（，），
故答案为（，）．
17．（1），； （2），； （3分一题）
18． （5分 ，化简正确3分）
19．（1），；（2）． （第一问2分，第二问3分合计5分）
20.（1）； （1分）
（2）小强设计的游戏规则不公平
画树状图如图：
（4分）
共有12个等可能的结果，两次摸出的小球球面上数字之和为奇数的结果有8种，和为偶数的结果有4种，
∴甲获胜的概率为，乙获胜的概率为，
∵23＞， （5分）
∴小强设计的游戏规则不公平． （6分）
（1）7.5, 8.0； （每空2分，共4分）
（2）该运动员本次试跳得分为84分． （6分）
22. (1) （ 2分）
(2) （4分）
(3) （ 6分）
23．（1）①； （1分）
②饲养场的宽为11米； （3分）
（2）设饲养场的面积为，的长为米．
①当点在线段上时，
根据（1）可得：，
∵，
∴当时，有最大值，最大值为，且当时，随的增大而减小．
∵当点在线段上时，需满足，
∴时，有最大值，最大值为（平方米）．
此时，满足点F在线段BC上． （5分）
②当点在线段的延长线上时，设DE为y米，
由（1）可得DB=GH=EF=x，DE=BF=y，，
∵BC=9，
∴．
∴．
∴．
解得．
∴．
∴．
∵，
∴当时，有最大值，最大值为（平方米）． （7分）
此时，满足点F在线段BC的延长线上．
∵，
∴饲养场的宽为8米时，饲养场的面积最大，最大面积为96平方米．
答：饲养场的宽为8米时，饲养场的面积最大，最大面积为96平方米． （8分）
24.（1）-3，6； （每空1分，共2分）
（2）； （ 5分 )
（3）x的值为1或或4．
（2），
，
∵，
∴，，
∴，
∴；
（3）当时，根据，
可得：，
解得：，（舍去）； (6分）
当时，根据，
可得：，
解得：，（舍去）； （7分）
当时，根据，
可得：，
解得：（舍去），； （8分）
综上所述，x的值为1或或4．
25．【详解】（1）解：依题意，，
解得：或；
答：这种服装每件销售价是元或元； （2分）
（2）设毛利润为，依题意，
，
∵，抛物线开口向下，
有最大值，当时，，
∴每件服装销售价元才能使每天的毛利润最大，最大毛利润是； （6分）
（3）设捐款后的剩余毛利润为，则，
依题意，
即
即，②
解方程①，
解得：，
∵抛物线开向下，，
∴，
②
解得：， （9分）
∵抛物线开向下，，
∴或，
∴或，
故答案为：或． （10分）
26．解：（1）由直线y＝x＋2可得，∴
∵，∴，即
将、代入抛物线解析式可得
，解得
故答案为：， (2分）
（2）由（1）得抛物线解析式为
过点作并延长交于点，过点作，设交于点，如下图：
则，
又∵
∴
又∵
∴
∴，即
联立直线与抛物线可得
，即
解得，
，即，
∴，
∴，即的最大值，即是的最大值
设，则
∵，
∴时，最大，为
此时，
故答案为：最大值为，， （6分）
（3）由（2）得，
，

又∵，都为锐角
∴
当在点左侧时，，此时以A，P，Q为顶点的三角形与△ABE不相似，所以在点右侧，
设，则
由题意可得：，，
当时，，即，解得，此时 （8分）
当时，，即，解得，此时 （10分）
综上所述，或 （方法较多，可以不用三角函数）
27．【详解】解：（1）令y=0，则0= a（x+2）（x－8）
∴x1=﹣2，x2=8
∴A（﹣2,0），B（8,0），AB=10
∵△ABC的面积为20
∴OC=4
∴C（0,4），把C代入抛物线解析式得：
a=， （1分）
根据A，B，C三点坐标可求得AC=,BC=
又AB=10
∴
∴△ABC是∠ACB为直角的直角三角形； （3分）
（2）由题意可得D（0，﹣4）
∵△ADP的面积最大，而AD长度固定，因此求点P在何处时到AD距离最大，过P作AD的平行线，则P到AD的距离是两条平行线之间的距离，
当平行线与抛物线相切时，即只有一个交点时距离最大，
∵A(﹣2,0)，D（0，﹣4）可求得AD：y=﹣2x－4
∴设过P点平行AD的直线为：y=﹣2x+b
联立
化简得：，
△=，
解得：b=，
∴y=﹣2x+
解得： ，把x=7代入y=﹣2x+
y=，P（7，）
∴当m=7时，△ADP面积有最大值； (5分）
（3）如图，当Q在BC的上方时即Q1
∵B（8,0）设BQ1：y=kx－8k
设BQ1与y轴的交点为G，过点C作CH⊥BQ1于点H，
易得△GOB∽△GHC，根据角平分线的性质得OB=OH=8,CH=OC=4
∴
∵OG=﹣8k，
∴GH=﹣4k，
∴GB=HG+HB=8－4k，
在Rt△OGB中，
解得：k1=0（舍去），k2=
∴BQ1：y=x+
又BQ与抛物线有交点，
∴x+=
整理解得：x1=8（舍去），x2=
当x=时，y=
∴Q1（，） （8分）
②当Q在BC下方时，由对称性可知，
BQ2：y= ，与抛物线有交点，
∴=
解得：x1=8（舍去），x2=
当x=﹣4时，y=
∴Q2（，） （10分）
综上Q的坐标为：Q（，）或Q （，）
难度系数
裁判
1#
2#
3#
4#
5#
6#
7#
3.5
打分
7.5
8.5
7.5
9.0
7.5
8.5
8.0
题号
1
2
3
4
5
6
7
8


答案
B
B
D
B
A
C
C
D