山东省日照市东港区曲阜师大附属实验学校2024-2025学年九年级上学期月考数学试卷（10月份）

这是一份山东省日照市东港区曲阜师大附属实验学校2024-2025学年九年级上学期月考数学试卷（10月份），共14页。试卷主要包含了单选题，解答题等内容，欢迎下载使用。
1．（3分）若关于x的方程（c﹣1）x|c|+1+9x﹣4＝0是一元二次方程，则c的值为（ ）
A．1B．﹣1C．2D．﹣2
2．（3分）抛物线y＝x2﹣4x﹣5的顶点坐标是（ ）
A．（2，1）B．（2，﹣9）C．（﹣2，1）D．（﹣2，﹣9）
3．（3分）对于抛物线y＝﹣2（x﹣3）2+10，下列说法错误的是（ ）
A．抛物线开口向下
B．当x＞3时，y＜10
C．抛物线与x轴有两个交点
D．当x＝3时，y有最小值为10
4．（3分）2022年北京冬奥会女子冰壶比赛，有若干支队伍参加了单循环比赛（每两队之间都赛一场），单循环比赛共进行了45场，共有多少支队伍参加比赛？设共有x支队伍参加比赛，则所列方程为（ ）
A．x（x+1）＝45B．＝45
C．x（x﹣1）＝45D．＝45
5．（3分）某农机厂四月份生产零件50万个，第二季度共生产零件182万个．设该厂五、六月份平均每月的增长率为x，那么x满足的方程是（ ）
A．50（1+x）2＝182
B．50+50（1+x）+50（1+x）2＝182
C．50（1+2x）＝182
D．50+50（1+x）+50（1+2x）＝182
6．（3分）若A（﹣4、y1），B（﹣1，y2），C（1，y3）为二次函数y＝x2+4x﹣5的图象上的三点，则y1，y2，y3的从小到大顺序是（ ）
A．y1＜y2＜y3B．y3＜y1＜y2C．y3＜y2＜y1D．y2＜y1＜y3
7．（3分）已知α、β是关于x的一元二次方程x2﹣（2m+3）x+m2＝0的两个不相等的实数根，且满足+＝1，则m的值是（ ）
A．3B．﹣1C．3或﹣1D．﹣3或1
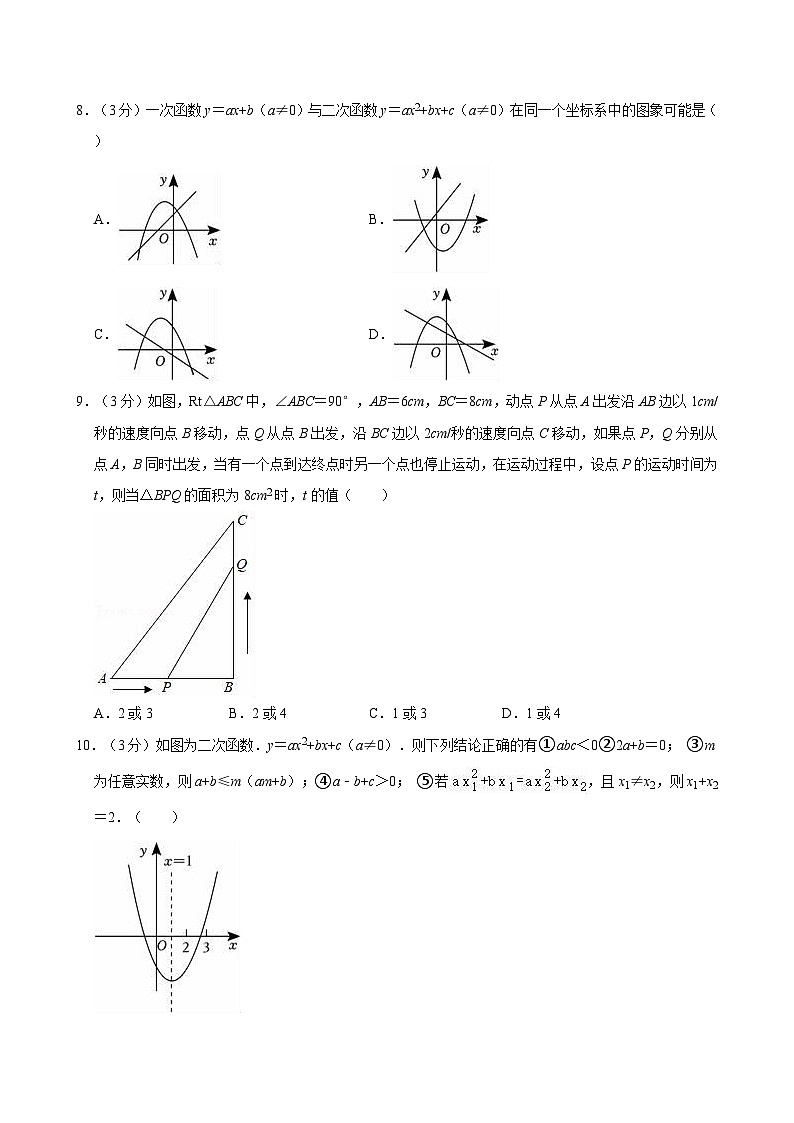
8．（3分）一次函数y＝ax+b（a≠0）与二次函数y＝ax2+bx+c（a≠0）在同一个坐标系中的图象可能是（ ）
A．B．
C．D．
9．（3分）如图，Rt△ABC中，∠ABC＝90°，AB＝6cm，BC＝8cm，动点P从点A出发沿AB边以1cm/秒的速度向点B移动，点Q从点B出发，沿BC边以2cm/秒的速度向点C移动，如果点P，Q分别从点A，B同时出发，当有一个点到达终点时另一个点也停止运动，在运动过程中，设点P的运动时间为t，则当△BPQ的面积为8cm2时，t的值（ ）
A．2或3B．2或4C．1或3D．1或4
10．（3分）如图为二次函数．y＝ax2+bx+c（a≠0）．则下列结论正确的有①abc＜0②2a+b＝0； ③m为任意实数，则a+b≤m（am+b）；④a﹣b+c＞0； ⑤若，且x1≠x2，则x1+x2＝2．（ ）
A．2个B．3个C．4个D．5个
一、单选题（每小题3分，共30分）
11．（3分）方程x2﹣8＝0的根是 ．
12．（3分）若将一个二次函数的图象向下平移2个单位，再向左平移3个单位，所得函数解析式是，那么这个函数解析式为 ．
13．（3分）已知抛物线y＝ax2+bx+c（a≠0）与x轴交于A，B两点，点A的坐标为（﹣1，0），抛物线的对称轴为直线x＝2，则线段AB的长为 ．
14．（3分）老师给出一个二次函数，甲、乙、丙三名同学各指出这个函数的一个性质．
甲：函数图象的顶点在x轴上；
乙：当x＜1时，y随x的增大而减小；
丙：该函数的开口大小、形状均与函数y＝x2的图象相同．
已知这三位同学的描述都正确，请你写出满足上述所有性质的一个二次函数表达式 ．
15．（3分）若菱形ABCD的一条对角线长为7，边AB的长为方程x2﹣6x+8＝0的一个根，则菱形ABCD的周长为 ．
16．（3分）设α，β是一元二次方程x2+3x﹣17＝0的两个根，则α2+5α+2β＝ ．
17．（3分）规定：两个函数y1，y2的图象关于y轴对称，则称这两个函数互为“Y函数”．例如：函数y1＝2x+2与y2＝﹣2x+2的图象关于y轴对称，则这两个函数互为“Y函数”．若函数y＝kx2+2（k﹣1）x+k﹣3（k为常数）的“Y函数”图象与x轴只有一个交点，则其“Y函数”的解析式为 ．
三、解答题（共′69分）
18．（10分）解方程：
（1）3x2﹣8x﹣4＝0；
（2）6+3x＝﹣5x（x+2）．
19．（10分）已知关于x的一元二次方程x2﹣（2m+3）x+m2+2＝0．
（1）若方程有实数根，求实数m的取值范围；
（2）若方程的两个根分别为x1、x2，且满足x12+x22＝31+x1x2，求实数m的值．
20．（10分）某农场要建一个矩形养鸡场，鸡场的一边靠墙，另外三边用木栅栏围成．已知墙长25m，木栅栏长47m，在与墙垂直的一边留出1m宽的出入口（另选材料建出入门）．求鸡场面积的最大值．
21．（12分）如图，已知抛物线y＝x2+bx+c经过A（﹣1，0），B（3，0）两点，与y轴交于点C．
（1）求抛物线解析式和顶点坐标；
（2）观察图象：
①当0＜x＜3时，直接写出y的取值范围；
②点P为抛物线上一点，若S△ABP＝24，求出此时P点的坐标．
22．（13分）某商品的进价为每件80元，售价为每件100元时，每天可卖出600件．市场调查反映，如果调整价格，一件商品每涨价1元，每天要少卖出10件．
（1）求每天所得的销售利润w（元）与每件涨价x（元）之间的函数关系式；
（2）求销售单价为多少元时，该商品每天的销售利润最大；
（3）商场的营销部在调控价格方面，提出了A，B两种营销方案．
方案A：每件商品涨价不超过18元；
方案B：每件商品的利润至少为41元．
请比较哪种方案的最大利润更高，并说明理由．
23．（14分）如图，抛物线经过A（﹣1，0），B（3，0），C（0，）三点．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．
2024-2025学年山东省日照市东港区曲阜师大附属实验学校九年级（上）月考数学试卷（10月份）
参考答案与试题解析
一、单选题（每小题3分，共30分）
1．【解答】解：∵关于x的方程（c﹣1）x|c|+1+9x﹣4＝0是一元二次方程，
∴|c|+1＝2，
∴|c|＝1，
∴c＝±1，
∵c﹣1≠0，
∴c≠1，
∴c＝﹣1，
故选：B．
2．【解答】解：由题意，∵抛物线为y＝x2﹣4x﹣5＝（x﹣2）2﹣9，
∴其顶点坐标为（2，﹣9）．
故选：B．
3．【解答】解：∵y＝﹣2（x﹣3）2+10，
∴抛物线开口向下，顶点坐标为（3，10），抛物线与x轴有2个交点，x≥3时y随x增大而减小，当x＝3时y有最大值为10，
∴选项A，B，C正确，D错误，
故选：D．
4．【解答】解：设共有x支队伍参加比赛，
依题意得：＝45，
故选：D．
5．【解答】解：依题意得五、六月份的产量为50（1+x）、50（1+x）2，
∴50+50（1+x）+50（1+x）2＝182．
故选：B．
6．【解答】解：∵A（﹣4、y1），B（﹣1，y2），C（1，y3）为二次函数y＝x2+4x﹣5的图象上的三点，
∴y1＝x2+4x﹣5＝（﹣4）2+4×（﹣4）﹣5＝﹣5；y2＝x2+4x﹣5＝（﹣1）2+4×（﹣1）﹣5＝﹣8；y3＝x2+4x﹣5＝12+4×1﹣5＝0，
∴y2＜y1＜y3．
故选：D．
7．【解答】解：∵α、β是关于x的一元二次方程x2﹣（2m+3）x+m2＝0的两个不相等的实数根，
∴α+β＝2m+3，αβ＝m2，
∴+＝＝＝1，
解得：m＝﹣1或m＝3，
经检验，m＝﹣1或m＝3均为原分式方程的解．
∵α、β是关于x的一元二次方程x2﹣（2m+3）x+m2＝0的两个不相等的实数根，
∴Δ＝[﹣（2m+3）]2﹣4m2＝12m+9＞0，
∴m＞﹣，
∴m＝3．
故选：A．
8．【解答】解：A、由抛物线可知，a＜0，x＝﹣＜0，得b＜0，由直线可知，a＞0，b＞0，故本选项错误；
B、由抛物线可知，a＞0，x＝﹣＞0，得b＜0，由直线可知，a＞0，b＞0，故本选项错误；
C、由抛物线可知，a＜0，x＝﹣＜0，得b＜0，由直线可知，a＜0，b＜0，故本选项正确；
D、由抛物线可知，a＜0，x＝﹣＜0，得b＜0，由直线可知，a＜0，b＞0，故本选项错误．
故选：C．
9．【解答】解：当运动时间为t秒时，BP＝（6﹣t）cm，BQ＝2t cm，
依题意得：（6﹣t）×2t＝8，
整理得：t2﹣6t+8＝0，
解得：t1＝2，t2＝4．
故选：B．
10．【解答】解：①抛物线开口方向向上，则a＞0．
抛物线对称轴位于y轴右侧，则a、b异号，即ab＜0．
抛物线与y轴交于y轴负半轴，则c＜0，
所以abc＜0．
故①错误；
②∵抛物线对称轴为直线x＝﹣＝1，
∴b＝﹣2a，即2a+b＝0，
故②正确；
③∵抛物线对称轴为直线x＝1，
∴函数的最小值为：a+b+c，
∴m为任意实数时，a+b≤m（am+b），即a+b+c＜am2+bm+c，
故③正确；
④∵抛物线与x轴的一个交点在（3，0）的左侧，而对称轴为直线x＝1，
∴抛物线与x轴的另一个交点在（﹣1，0）的右侧，
∴当x＝﹣1时，y＞0，
∴a﹣b+c＞0，
故④正确；
⑤∵，
∴a+bx1﹣a﹣bx2＝0，
∴a（x1+x2）（x1﹣x2）+b（x1﹣x2）＝0，
∴（x1﹣x2）[a（x1+x2）+b]＝0，
而x1≠x2，
∴a（x1+x2）+b＝0，即x1+x2＝﹣，
∵b＝﹣2a，
∴x1+x2＝2，
故⑤正确．
综上所述，正确的有②③④⑤，共4个；
故选：C．
一、单选题（每小题3分，共30分）
11．【解答】解：∵x2﹣8＝0，
∴x＝±2，
故答案为：x＝±2
12．【解答】解：y＝（x﹣3）2+2向下平移2个单位，再向左平移3个单位得y＝x2．
故答案为：y＝（x﹣3）2+2．
13．【解答】解：∵点A的坐标为（﹣1，0），抛物线的对称轴为直线x＝2，
又2﹣（﹣1）＝3，
∴点B的横坐标为2+3＝5，
∴B（5，0）．
∴AB＝5﹣（﹣1）＝6．
故答案为：6．
14．【解答】解：∵函数图象的顶点在x轴上，当x＜1时，y随x的增大而减小；
∴可设顶点坐标为（1，0），对称轴为直线x＝1，
∵该函数的开口大小、形状均与函数y＝x2的图象相同，
∴二次项系数为1，
∴满足条件二次函数表达式可为y＝（x﹣1）2．
故答案为y＝（x﹣1）2．
15．【解答】解：x2﹣6x+8＝0，
（x﹣4）（x﹣2）＝0，
x﹣4＝0或x﹣2＝0，
解得x1＝4，x2＝2，
当AB＝2时，2+2＜7，不合题意舍去；
当AB＝4时，菱形ABCD的周长＝4×4＝16．
故答案为：16．
16．【解答】解：∵α，β是一元二次方程x2+3x﹣17＝0的两个根，
∴α2+3α﹣17＝0，α+β＝﹣3，
∴α2+3α＝17，
∴α2+5α+2β＝（α2+3α）+2（α+β）＝17﹣6＝11．
故答案为：11．
17．【解答】解：∵函数y＝kx2+2（k﹣1）x+k﹣3（k为常数）的“Y函数”图象与x轴只有一个交点，
∴函数y＝kx2+2（k﹣1）x+k﹣3（k为常数）的图象与x轴也只有一个交点，
当k＝0时，函数解析式为y＝﹣2x﹣3，它的“Y函数”解析式为y＝2x﹣3，它们的图象与x轴只有一个交点，
当k≠0时，此函数是二次函数，
∵它们的图象与x轴都只有一个交点，
∴它们的顶点分别在x轴上，
∴＝0，
解得：k＝﹣1，
∴原函数的解析式为y＝﹣x2﹣4x﹣4＝﹣（x+2）2，
∴它的“Y函数”解析式为y＝﹣（x﹣2）2＝﹣x2+4x﹣4，
综上，“Y函数”的解析式为y＝2x﹣3或y＝﹣x2+4x﹣4，
故答案为：y＝2x﹣3或y＝﹣x2+4x﹣4．
三、解答题（共′69分）
18．【解答】解：（1）3x2﹣8x﹣4＝0，
∵a＝3，b＝﹣8，c＝﹣4，
∴Δ＝（﹣8）2﹣4×3×（﹣4）＝16×7＞0，
∴x＝＝，
所以x1＝，x2＝；
（2）6+3x＝﹣5x（x+2），
3（x+2）+5x（x+2）＝0，
（x+2）（3+5x）＝0，
x+2＝0或3+5x＝0，
所以x1＝﹣2，x2＝﹣．
19．【解答】解：（1）∵方程x2﹣（2m+3）x+m2+2＝0有实数根，
∴Δ＝[﹣（2m+3）]2﹣4（m2+2）＝12m+1≥0，
解得：m≥﹣．
（2）∵方程x2﹣（2m+3）x+m2+2＝0的两个根分别为x1、x2，
∴x1+x2＝2m+3，x1•x2＝m2+2，
∵x12+x22＝31+x1x2，
∴﹣2x1•x2＝31+x1x2，即m2+12m﹣28＝0，
解得：m1＝2，m2＝﹣14（舍去），
∴实数m的值为2．
20．【解答】解：设矩形鸡场与墙垂直的一边长为x m，则与墙平行的一边长为（47﹣2x+1）m，由题意可得：
y＝x（47﹣2x+1），
即y＝﹣2（x﹣12）2+288，
由题意，
解得11.5≤x＜24，
∵﹣2＜0，
∴当x＝12时，y有最大值为288，
当x＝12时，47﹣x﹣（x﹣1）＝24＜25（符合题意），
∴鸡场的最大面积为288m2．
21．【解答】解：（1）∵抛物线y＝x2+bx+c经过A（﹣1，0），B（3，0）两点，
∴，
解得：，
∴抛物线的解析式为y＝x2﹣2x﹣3，
∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴顶点坐标为（1，﹣4）；
（2）①∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴抛物线开口向上，对称轴为直线x＝1，
∴当x＜1时，y随着x的增大而减小，当x＞1时，y随着x的增大而增大，
∴当0＜x＜3时，当x＝1时，y有最小值为﹣4，当x＝3时，y＝（3﹣1）2﹣4＝0，当x＝0时，y＝（0﹣1）2﹣4＝﹣3，
∴当0＜x＜3时，y的取值范围为﹣4≤y＜0；
②∵A（﹣1，0），B（3，0），
∴AB＝4，
∵S△ABP＝24，
∴，
∴|yP|＝12，
∵抛物线顶点坐标为（1，﹣4），
∴yP＝12，
当yP＝12时，x2﹣2x﹣3＝12，
解得：x1＝﹣3，x2＝5，
∴P（﹣3，12）或（5，12）．
22．【解答】解：（1）w＝（100+x﹣80）（600﹣10x）
＝﹣10x2+400x+12000
＝﹣10（x﹣20）2+16000，
∴销售利润w与每件涨价x之间的函数关系式为w＝﹣10（x﹣20）2+16000（0≤x≤60）；
（2）由（1）知：w＝﹣10（x﹣20）2+16000，
∵x＝﹣10＜0，
∴抛物线开口向下，w有最大值，
∴当x＝20时，最大值为16000，
此时销售单价为20+100＝120（元），
∴销售单价为120元时，该商品每天的销售利润最大；
（3）w＝﹣10（x﹣20）2+16000，
二次函数的对称轴为直线x＝20，抛物线开口向下，
∴当x＜20时，w随x的增大而增大，当x＞20时，w随x的增大而减小
方案A：∵x≤18，
∴0≤x≤18，
∴当x＝18时，w有最大值，最大值为：﹣10（18﹣20）2+16000＝15960（元），
方案B：∵100+x﹣80≥41，
∴x≥21，600﹣10x≥0，
∴21≤x≤60，
∴当x＝21时，w有最大值，最大值：﹣10（21﹣20）2+16000＝15990（元），
∵15990＞15960，
∴方案B最大利润更高．
23．【解答】解：（1）设抛物线的解析式为y＝ax2+bx+c（a≠0），
∵A（﹣1，0），B（5，0），C（0，）三点在抛物线上，
∴，
解得．
∴抛物线的解析式为：．
（2）∵抛物线的解析式为，
∴其对称轴为直线：．
连接BC，设直线BC的解析式为y＝kx+b（k≠0），
∵B（3，0），C（0，），
∴解得．
∴直线BC的解析式为．
当x＝1时，．
∴P（1，1）；
（3）存在．如图2所示．
①当点N在x轴上方时，
∵抛物线的对称轴为直线x＝1，C（0，），
∴N1（2，）；
②当点N在x轴下方时，
如图，过点N2作N2D⊥x轴于点D，
∴△AN2D≌△M2CO．
∴N2D＝OC＝，即N2点的纵坐标为．
∴x2+x+＝．解得x＝或x＝，
∴N2（，），N3（，）．
综上所述，点N的坐标为（2，），（，），（，）．