
广西省来宾市2024年数学九上开学达标测试试题【含答案】
展开
这是一份广西省来宾市2024年数学九上开学达标测试试题【含答案】,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)在分式(a,b为正数)中,字母a,b值分别扩大为原来的3倍,则分式的值( )
A.不变B.缩小为原来的
C.扩大为原来的3倍D.不确定
2、(4分)对某小区20户家庭某月的节约用水情况进行分组统计,结果如下表:
由上表可知,这20户家庭该月节约用水量的平均数是( )
A.1.8tB.2.3tC.2.5tD.3 t
3、(4分)在中,平分,,则的周长为( )
A.B.C.D.
4、(4分)下列所述图形中,既是中心对称图形,又是轴对称图形的是( )
A.矩形B.平行四边形C.正五边形D.正三角形
5、(4分)若直线经过第一、二、四象限,则化简的结果是 ( )
A.2 kB.2 kC.k 2D.不能确定
6、(4分)我市某楼盘准备以每平方6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过连续两次下调后,决定以每平方4860元的均价开盘销售,则平均每次下调的百分率是( ).
A.8%B.9%C.10%D.11%
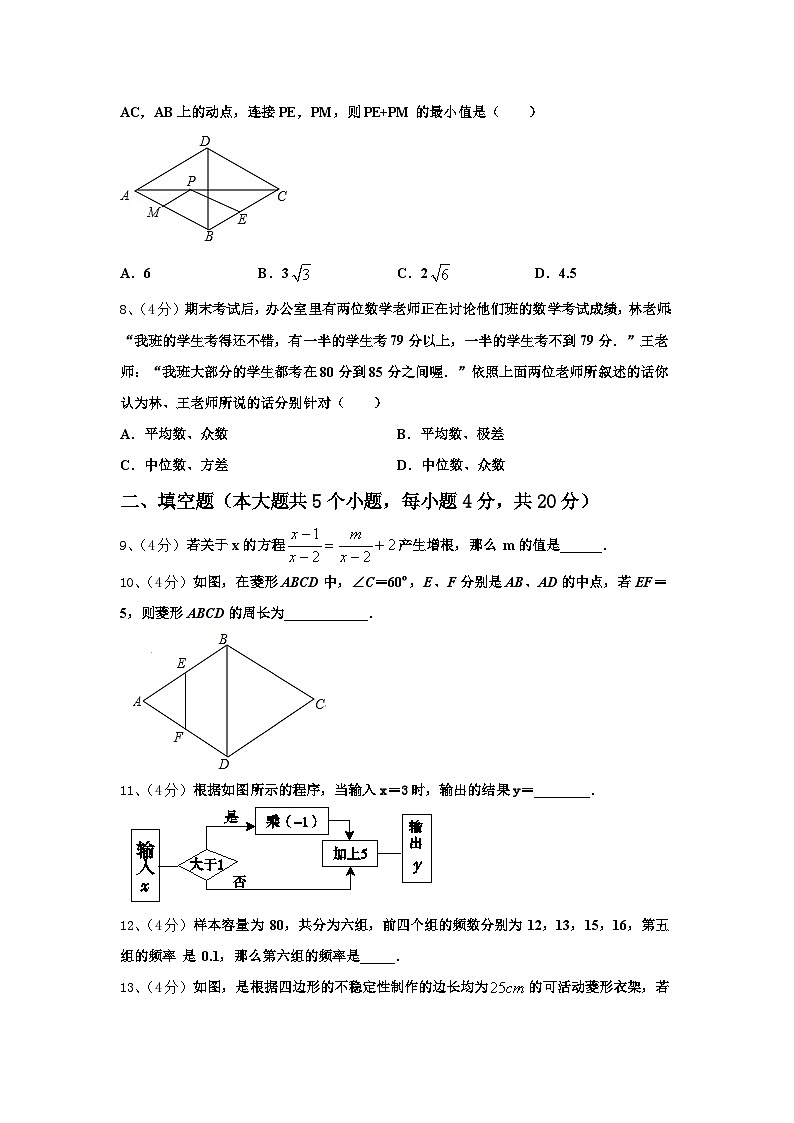
7、(4分)如图,在菱形ABCD中,AC=6,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
A.6B.3C.2D.4.5
8、(4分)期末考试后,办公室里有两位数学老师正在讨论他们班的数学考试成绩,林老师:“我班的学生考得还不错,有一半的学生考79分以上,一半的学生考不到79分.”王老师:“我班大部分的学生都考在80分到85分之间喔.”依照上面两位老师所叙述的话你认为林、王老师所说的话分别针对( )
A.平均数、众数B.平均数、极差
C.中位数、方差D.中位数、众数
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)若关于x的方程产生增根,那么 m的值是______.
10、(4分)如图,在菱形ABCD中,∠C=60º,E、F分别是AB、AD的中点,若EF=5,则菱形ABCD的周长为____________.
11、(4分)根据如图所示的程序,当输入x=3时,输出的结果y=________.
12、(4分)样本容量为 80,共分为六组,前四个组的频数分别为 12,13,15,16,第五组的频率 是 0.1,那么第六组的频率是_____.
13、(4分)如图,是根据四边形的不稳定性制作的边长均为的可活动菱形衣架,若墙上钉子间的距离,则=______度.
三、解答题(本大题共5个小题,共48分)
14、(12分)如图,将一矩形纸片OABC放在平面直角坐标系中,,,.动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
(1)OP =____________, OQ =____________;(用含t的代数式表示)
(2)当时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.
①求点D的坐标;
②如果直线y = kx + b与直线AD平行,那么当直线y = kx + b与四边形PABD有交点时,求b 的取值范围.
15、(8分)如图,平行四边形ABCD的四个内角的平分线相交成四边形EFGH,求证:
(1)EG=HF.
(2)EG=BC-AB.
16、(8分)甲、乙两名射击运动员进行射击比赛,两人在相同的条件下各射击10次,射击的成绩如图所示.根据图中信息,解答下列问题:
(1)算出乙射击成绩的平均数;
(2)经计算,甲射击成绩的平均数为8,乙射击成绩的方差为1.2,请你计算出甲射击成绩的方差,并判断谁的射击成绩更加稳定.
17、(10分)如图,要在长、宽分别为50米、40米的矩形草坪内建一个正方形的观赏亭.为方便行人,分别从东,南,西,北四个方向修四条宽度相同的矩形小路与亭子相连,若小路的宽是正方形观赏亭边长的,小路与观赏亭的面积之和占草坪面积的,求小路的宽.
18、(10分)将一矩形纸片放在直角坐标系中,为原点,点在轴上,点在轴上,.
(1)如图1,在上取一点,将沿折叠,使点落在边上的点处,求直线的解析式;
(2)如图2,在边上选取适当的点,将沿折叠,使点落在边上的点处,过作于点,交于点,连接,判断四边形的形状,并说明理由;
(3)、在(2)的条件下,若点坐标,点在直线上,问坐标轴上是否存在点,使以为顶点的四边形是平行四边形,若存在,请直接写出点坐标;若不存在,请说明理由.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)已知一个反比例函数的图象与正比例函数的图象有交点,请写出一个满足上述条件的反比例函数的表达式:__________________.
20、(4分)已知一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数的解析式为 .
21、(4分)有一组数据如下:3、7、4、6、5,那么这组数据的方差是_____.
22、(4分)已知:在▱ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则▱ABCD的面积是_____.
23、(4分)如图,平行四边形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件________使其成为菱形(只填一个即可).
二、解答题(本大题共3个小题,共30分)
24、(8分)如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.
(1)求证:AG=C′G;
(2) 求△BDG的面积.
25、(10分)在如图所示的平面直角坐标系中,直线AB:y=k1x+b1与直线AD:y=k2x+b2相交于点A(1,3),且点B坐标为(0,2),直线AB交x轴负半轴于点C,直线AD交x轴正半轴于点D.
(1)求直线AB的函数解析式;
(2)若△ACD的面积为9,解不等式:k2x+b2>0;
(3)若点M为x轴一动点,当点M在什么位置时,使AM+BM的值最小?求出此时点M的坐标.
26、(12分)已知:如图,在▱ABCD中,AE⊥BC,CF⊥AD,垂足分别为E、F,AE、CF分别与BD相交于点G、H,联结AH、CG.
求证:四边形AGCH是平行四边形.
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、B
【解析】
把a和b的值扩大大为原来的3倍,代入后根据分式的基本性质即可求出答案.
【详解】
解:把a和b的值扩大大为原来的3倍,得
= ,
∴分式的值缩小为原来的.
故选:B.
本题考查分式的基本性质,解题的关键是熟练运用分式的基本性质,本题属于基础题型.
2、B
【解析】
根据每组的组中值利用加权平均数的定义列式计算即可得.
【详解】
解:由上表可知,这20户家庭该月节约用水量的平均数是
=2.3(t),
故选B.
本题考查了加权平均数,掌握加权平均数的计算公式是解题的关键.
3、C
【解析】
首先证得△ADC≌△ABC,由全等三角形的性质易得AD=AB,由菱形的判定定理得▱ABCD为菱形,由菱形的性质得其周长.
【详解】
解:如图:
∵AC平分∠DAB,
∴∠DAC=∠BAC.
∵四边形ABCD为平行四边形,
∴∠B=∠D.
在△ADC和△ABC中,
,
∴△ADC≌△ABC,
∴AD=AB,
∴四边形ABCD为菱形,
∴AD=AB=BC=CD=3,
∴▱ABCD的周长为:3×4=1.
故选:C
本题主要考查了全等三角形的判定及菱形的判定及性质,找出判定菱形的条件是解答此题的关键.
4、A
【解析】
试题分析:在一个平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形与另一个图形重合,这样的图形叫做中心对称图形.根据定义可得:平行四边形只是中心对称图形,正五边形、正三角形只是轴对称图形,只有矩形符合.
考点:轴对称图形与中心对称图形.
5、B
【解析】
根据一次函数图像的性质,函数图像过一、二、四象限,则k<0.b>0.并考察了绝对值的性质.
【详解】
∵直线y=kx+2经过第一、二、四象限,
∴k<0,
∴k-2<0,
∴|k-2|=2-k,
故选B.
本题考查了一次函数图像的性质,难点在于根据函数所过象限确定系数的值.
6、C
【解析】
分析:设平均每次下调的百分率为x,则两次降价后的价格为6000(1-x)2,根据降低率问题的数量关系建立方程求出其解即可.
详解:设平均每次下调的百分率为x,由题意,得
6000(1-x)2=4860,
解得:x1=0.1,x2=1.9(舍去).
答:平均每次下调的百分率为10%.
故选C.
点睛:本题考查了一元二次方程的应用,降低率问题的数量关系的运用,一元二次方程的解法的运用,解答时根据降低率问题的数量关系建立方程是关键.
7、C
【解析】
【分析】如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P,由PE+PM=PE′+PM=E′M知点P、M即为使PE+PM取得最小值的点,利用S菱形ABCD= AC•BD=AB•E′M求得E′M的长即可得答案.
【详解】如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P,
则点P、M即为使PE+PM取得最小值的点,
则有PE+PM=PE′+PM=E′M,
∵四边形ABCD是菱形,
∴点E′在CD上,
∵AC=6,BD=6,
∴AB=,
由S菱形ABCD=AC•BD=AB•E′M得×6×6=3•E′M,
解得:E′M=2,
即PE+PM的最小值是2,
故选C.
【点睛】本题考查了轴对称——最短路径问题,涉及到菱形的性质、勾股定理等,确定出点P的位置是解题的关键.
8、D
【解析】
试题分析:∵有一半的学生考79分以上,一半的学生考不到79分,
∴79分是这组数据的中位数,
∵大部分的学生都考在80分到85分之间,
∴众数在此范围内.
故选D.
考点:统计量的选择.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、1
【解析】
分式方程去分母转化为整式方程,根据分式方程有增根得到x-2=0,将x=2代入整式方程计算即可求出m的值.
【详解】
分式方程去分母得:x−1=m+2x−4,
由题意得:x−2=0,即x=2,
代入整式方程得:2−1=m+4−4,
解得:m=1.
故答案为:1.
此题考查分式方程的增根,解题关键在于掌握分式方程中增根的意义.
10、1
【解析】
先根据菱形的性质可得,再根据线段中点的定义可得,然后根据等边三角形的判定与性质可得,从而可得,最后根据菱形的周长公式即可得.
【详解】
四边形ABCD是菱形,
点E、F分别是AB、AD的中点
又
是等边三角形
则菱形ABCD的周长为
故答案为:1.
本题考查了菱形的性质、等边三角形的判定与性质等知识点,熟练掌握菱形的性质是解题关键.
11、1
【解析】
根据自变量与函数值的对应关系,可得相应的函数值.
【详解】
当x=3时,y=﹣3+5=1.
故答案为:1.
本题考查了函数值,将自变量的值代入相应的函数关系式是解题的关键.
12、0.2.
【解析】
首先根据频率=频数÷总数,计算从第一组到第四组的频率之和,再进一步根据一组数据中,各组的频率和是1,进行计算.
【详解】
解:根据题意得:第一组到第四组的频率之和是,又因为第五组的频率是 0.1,所以第六组的频率是.
故答案为0.2.
本题考查的是频率分布直方图,这类题目主要涉及以下三个计算公式:频率=频数÷样本容量,各组的频率之和为1,各组的频数之和=样本容量.
13、1
【解析】
根据题意可得,AB和菱形的两边构成的三角形是等边三角形,可得∠A=60°,所以,∠1=1°
【详解】
解:如图,连接AB.
∵菱形的边长=25cm,AB=BC=25cm
∴△AOB是等边三角形
∴∠AOB=60°,
∴∠AOD=1°
∴∠1=1°.
故答案为:1.
本题主要考查菱形的性质及等边三角形的判定的运用.
三、解答题(本大题共5个小题,共48分)
14、(1)6-t; t+(2)①D(1,3) ②3≤b≤
【解析】
(1)根据OA的长以及点P运动的时间与速度可表示出OP的长,根据Q点的运动时间以及速度即可得OQ的长;
(2)①根据翻折的性质结合勾股定理求得CD长即可得;
②先求出直线AD的解析式,然后根据直线y=kx+b与直线AD平行,确定出k=,从而得表达式为:,根据直线与四边形PABD有交点,把点P、点B坐标分别代入求出b即可得b的取值范围.
【详解】
(1)由题意可知AP=t,所以OP=OA-AP=6-t,
根据Q点运动秒时,动点P出发,所以OQ=t+,
故答案为6-t, t+;
(2)①当t=1时,OQ=,
∵C(0,3),
∴OC=3,
∴CQ=OC-OQ=,
∵△OPQ沿PQ翻折得到△DPQ,
∴QD = OQ =,
在Rt△CQD中,有CD2=DQ2-CQ2,所以CD=1,
∵四边形OABC是矩形,
∴D(1,3);
②设直线AD的表达式为:(m≠0),
∵点A(6,0),点D(1,3),
∴,
解得,
∴直线AD的表达式为:,
∵直线y=kx+b与直线AD平行,
∴k=,
∴表达式为:,
∵直线与四边形PABD有交点,
∴当过点P(5,0)时,解得:b=3,
∴当过点B(6,3)时,解得:b=,
∴3≤b≤.
本题考查了矩形的性质、折叠的性质、勾股定理、一次函数的应用等,综合性较强,有一定的难度,熟练掌握相关性质与定理以及待定系数法是解题的关键.
15、(1)见详解;(2)见详解.
【解析】
(1)利用三个内角等于90°的四边形是矩形,即可证明;
(2)延长AF交BC于M,通过全等得到AB=BM,然后证明四边形EMCG是平行四边形,得到EG=CM,即可得证.
【详解】
解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分别平分∠ABC与∠BCD,
∴∠HBC=∠ABC,∠HCB=∠BCD,
∴∠HBC+∠HCB=(∠ABC+∠BCD)=×180°=90°,
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四边形EFGH是矩形,
∴EG=HF;
(2)如图,延长AF交BC于M,
由(1)中可知AE⊥AF,即∠BEA=∠BEM=90°,
在Rt△ABE和Rt△MBE中,
,
∴△ABE≌△MBE,
∴AB=MB,AE=EM,
由于四边形ABCD是平行四边形,
∴∠ABC=∠ADC,AB=CD
∵BH,DF分别平分∠ABC与∠ADC,
∴∠ABE=∠CDG,
在Rt△ABE和Rt△CDG中,
,
∴△ABE≌△CDG,
∴CG=AE,
∴CG=EM,
由于四边形EFGH是矩形,
∴EM∥CG,
∴四边形EMCG是平行四边形,
∴EG=MC,
由于MC=BC-BM,
∴EG=BC-AB.
本题考查了矩形的判定,平行四边形的判定和性质,角平分线的定义,熟练掌握判定方法是解题的关键.
16、(1)8;(2)乙.
【解析】
(1)用乙10次射击的成绩之和除以10即可得;
(2)根据方差的计算方法求出甲的方差,方差小的成绩更加稳定.
【详解】
解:(1);
(2),
∵;
∴乙的射击成绩更稳定.
故答案为(1)8;(2)乙.
本题考查了求平均数和方差,以及利用方差做判断,方差越小,数据的波动越小,更稳定.
17、小路的宽为2米.
【解析】
根据“小路与观赏亭的面积之和占草坪面积的”,建立方程求解即可得出结论.
【详解】
设小路的宽为x米,
由题意得,(5x)2+(40+50)x﹣2×x×5x=×40×50
解得,x=2或x=﹣8(不合题意,舍去)
答:小路的宽为2米.
考查一元二次方程的应用,读懂题目,找出题目中的等量关系列出方程是解题的关键.
18、(1);(2)四边形为菱形,理由详见解析;(3)以为顶点的四边形是平行四边形时,点坐标或或
【解析】
(1)根据题意求得点E的坐标,再代入,把代入得到,即可解答
(2)先由折叠的性质得出,由平行线的性质得出 ,即四边形为菱形.
(3)为顶点的四边形是平行四边形时,点坐标或或.
【详解】
解:(1)如图1中,
,是由翻折得到,
,
在中,,
,设,
在中,,解得,
,
设直线的解析式为,把代入得到,
直线的解析式为.
(2)如图2中,四边形为菱形,
理由:是由翻折得到,
,.
,
,而
.四边形为菱形.
(3)以为顶点的四边形是平行四边形时,
点坐标或或.
本题考查四边形综合,根据题意做辅助线和判断等量关系列出方程是解题关键.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、
【解析】
写一个经过一、三象限的反比例函数即可.
【详解】
反比例函数与有交点.
故答案为:.
本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法求函数解析式.
20、y=-x+1
【解析】
由函数的图象与直线y=-x+1平行,可得斜率,将点(8,2)代入即可人求解.
解:设所求一次函数的解析式为 y=kx+b,
∵函数的图象与直线y=-x+1平行,
∴k=-1,
又过点(8,2),有2=-1×8+b,
解得b=1,
∴一次函数的解析式为y=-x+1,
故答案为y=-x+1.
21、1
【解析】
试题分析:平均数为:(3+7+4+6+5)÷5=5,
S1=×[(3﹣5)1+(7﹣5)1+(4﹣5)1+(6﹣5)1+(5﹣5)1]
=×(4+4+1+1+0)
=1.
故答案为1.
点睛:本题考查方差的定义:一般地,设n个数据x1,x1,…xn的平均数为,则方差S1=[(x1-)1+(x1-)1+…+(xn-)1],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
22、1
【解析】
分析:利用平行四边形的性质可证明△AOF≌△COE,所以可得△COE的面积为3,进而可得△BOC的面积为8,又因为△BOC的面积=▱ABCD的面积,进而可得问题答案.
详解::∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAC=∠BCA,∠AEF=∠CFE,
又∵AO=CO,
在△AOE与△COF中
∴△AOE≌△COF
∴△COEF的面积为3,
∵S△BOF=5,
∴△BOC的面积为8,
∵△BOC的面积=▱ABCD的面积,
∴▱ABCD的面积=4×8=1,
故答案为1.
点睛:本题考查了平行四边形的性质及全等三角形的判定,解答本题需要掌握两点:①平行四边形的对边相等且平行,②全等三角形的对应边、对应角分别相等.
23、AC⊥BC或∠AOB=90°或AB=BC(填一个即可).
【解析】
试题分析:根据菱形的判定定理,已知平行四边形ABCD,添加一个适当的条件为:AC⊥BC或∠AOB=90°或AB=BC使其成为菱形.
考点:菱形的判定.
二、解答题(本大题共3个小题,共30分)
24、(1)见解析;(2)
【解析】
(1)根据矩形的性质可得AD=BC,AB=DC,AD∥BC,∠BAD=90°,从而得出∠GDB=∠DBC,然后根据折叠的性质可得BC= BC′,∠GBD=∠DBC,从而得出AD= BC′,∠GBD=∠GDB,然后根据等角对等边可得GD=GB,即可证出结论;
(2)设GD=GB=x,利用勾股定理列出方程即可求出GD的长,然后根据三角形的面积公式求面积即可.
【详解】
(1)证明:∵四边形ABCD为矩形
∴AD=BC,AB=DC,AD∥BC,∠BAD=90°
∴∠GDB=∠DBC
由折叠的性质可得BC= BC′,∠GBD=∠DBC
∴AD= BC′,∠GBD=∠GDB
∴GD=GB
∴AD-GD= BC′-GB
∴AG=C′G;
(2)解:设GD=GB=x,则AG=AD-GD=8-x
在Rt△ABG中
即
解得:
即
∴S△BDG=
此题考查的是矩形的性质、折叠的性质、等腰三角形的判定、勾股定理和求三角形的面积,掌握矩形的性质、折叠的性质、等角对等边、利用勾股定理解直角三角形是解决此题的关键.
25、(1)y=x+2;(2)x<4;(3)(,0).
【解析】
(1)将点A、B两点代入,即可求解析式;
(2)令y=0,求出C点坐标,由三角形ACD的面积是9,求出D点坐标,结合图象即可求解;
(3)作点B关于x轴的对称点E(0,-2),连接AE交x轴于点M,设直线AE解析式为y=kx+b,确定AE的解析式即可求M点坐标.
【详解】
解:(1)把A、B两点代入,得,
解得,
故直线AB的函数解析式为y=x+2;
(2)令y=x+2=0得x=-2,
∴C(-2,0).
又∵△ACD的面积为9,
∴3×CD=9,
∴CD=6,
∴D点坐标(4,0),
由图象得不等式的解集为:x<4;
(3)作点B关于x轴的对称点E(0,-2),连接AE交x轴于点M,
设直线AE解析式为y=kx+b,
∴,
∴,
∴y=5x-2,
当y=0时,x=,故点M的坐标为(,0).
本题考查一次函数的图象及性质待定系数法求函数解析式,轴对称的应用;熟练掌握待定系数法求函数解析式的方法,利用轴对称求最短距离是解题的关键.
26、证明见解析.
【解析】
法1:由平行四边形对边平行,且CF与AD垂直,得到CF与BC垂直,根据AE与BC垂直,得到AE与CF平行,得到一对内错角相等,利用等角的补角相等得到∠AGB=∠DHC,根据AB与CD平行,得到一对内错角相等,再由AB=CD,利用AAS得到三角形ABG与三角形CDH全等,利用全等三角形对应边相等得到AG=CH,利用一组对边平行且相等的四边形为平行四边形即可得证;
法2:连接AC,与BD交于点O,利用平行四边形的对角线互相平分得到OA=OC,OB=OD,再由AB与CD平行,得到一对内错角相等,根据CF与AD垂直,AE与BC垂直,得一对直角相等,利用ASA得到三角形ABG与三角形CDH全等,利用全等三角形对应边相等得到BG=DH,根据等式的性质得到OG=OH,利用对角线互相平分的四边形为平行四边形即可得证.
证明:在□ABCD中,AD∥BC,AB∥CD,
∵CF⊥AD,∴CF⊥BC,
∵AE⊥BC,∴AE∥CF,即AG∥CH,∴∠AGH=∠CHG,
∵∠AGB=180°﹣∠AGH,∠DHC=180°﹣∠CHG,
∴∠AGB=∠DHC,
∵AB∥CD,∴∠ABG=∠CDH,∴△ABG≌CDH,
∴AG=CH,
∴四边形AGCH是平行四边形;
法2:连接AC,与BD相交于点O,
在□ABCD中,AO=CO,BO=DO,∠ABE=∠CDF,AB∥CD,
∴∠ABG=∠CDH,
∵CF⊥AD,AE⊥BC,
∴∠AEB=∠CFD=90°,
∴∠BAG=∠DCH,
∴△ABG≌CDH,
∴BG=DH,
∴BO﹣BG=DO﹣DH,
∴OG=OH,
∴四边形AGCH是平行四边形.
“点睛”此题考查了平行四边形的判定与性质,熟练掌握平式子变形的判定与性质是解本题的关键.
题号
一
二
三
四
五
总分
得分
节约用水量x(t)
0.5≤x<1.5
1.5≤x<2.5
2.5≤x<3.5
3.5≤x<4.5
户数
6
4
8
2
相关试卷
这是一份广西省来宾市名校2024-2025学年数学九上开学达标检测试题【含答案】,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份广西省贵港市2024年数学九上开学质量检测试题【含答案】,共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2025届广西省来宾市名校九上数学开学统考试题【含答案】,共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









