河南省周口市商水县化河乡第一初级中学2023-2024学年八年级上学期月考数学试卷（12月份）

这是一份河南省周口市商水县化河乡第一初级中学2023-2024学年八年级上学期月考数学试卷（12月份），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.8的立方根为( )
A. B. C. 2D.
2.若三角形的三边长分别等于下列各组数，则能构成直角三角形的是( )
A. 1，2，3B. 3，4，5C. 2，3，5D. 6，8，12
3.下列选项中，可以用来说明命题“若，则”是假命题的反例是( )
A. B. C. D.
4.下列运算错误的是( )
A. B. C. D.
5.如图，已知，那么添加下列一个条件后，仍无法判定≌的是( )
A.
B.
C.
D.
6.若，则的值为( )
A. B. C. 0D. 2
7.如图，OC平分，点P是射线OC上一点，于点M，点N是射线OA上的一个动点.若，则PN的长度不可能是( )
A. 3
B. 4
C. 5
D. 6
8.将长、宽分别为x、y的四个完全一样的长方形，拼成如图所示的两个正方形，则这个图形可以用来解释的代数恒等式是( )
A.
B.
C.
D.
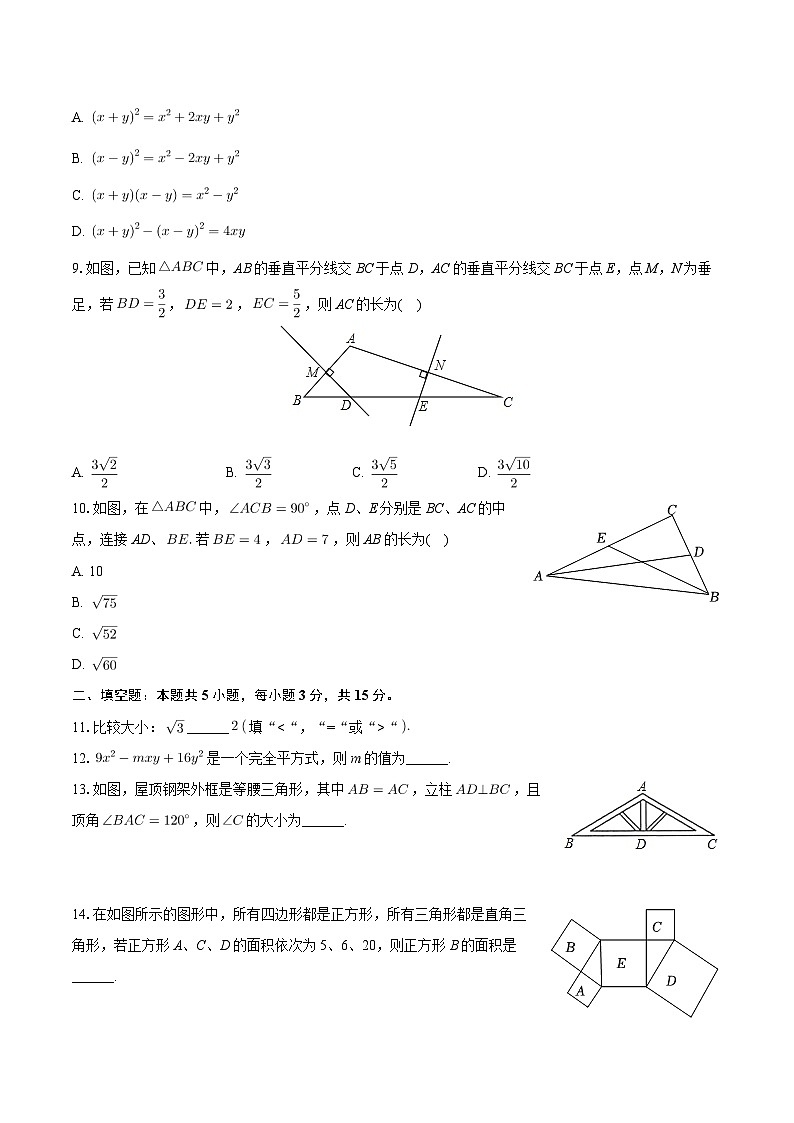
9.如图，已知中，AB的垂直平分线交BC于点D，AC的垂直平分线交BC于点E，点M，N为垂足，若，，，则AC的长为( )
A. B. C. D.
10.如图，在中，，点D、E分别是BC、AC的中点，连接AD、若，，则AB的长为( )
A. 10
B.
C.
D.
二、填空题：本题共5小题，每小题3分，共15分。
11.比较大小：______填““
12.是一个完全平方式，则m的值为______.
13.如图，屋顶钢架外框是等腰三角形，其中，立柱，且顶角，则的大小为______.
14.在如图所示的图形中，所有四边形都是正方形，所有三角形都是直角三角形，若正方形A、C、D的面积依次为5、6、20，则正方形B的面积是______.
15.如图，在中，，，，动点P从点B出发沿射线BA以的速度运动．则当运动时间______s时，为直角三角形．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.本小题12分
计算：；
计算：；
因式分解：；
因式分解
17.本小题11分
计算：；
计算：；
先化简，再求值：，其中，
18.本小题8分
如图，在中，，，，DE是AB的垂直平分线，DE分别交AC，AB于点E，
求证：是直角三角形；
求AE的长.
19.本小题8分
小明制作了一张面积为的正方形贺卡想寄给朋友.现有一个长方形信封如图所示，长、宽之比为3：2，面积为
求长方形信封的长和宽；
小明能将贺卡不折叠就放入此信封吗？请通过计算给出判断.
20.本小题8分
如图所示，已知等腰中，，与互余，
试说明：≌；
若，，求EF的长度.
21.本小题9分
如图，中，
作的平分线，交BC于点D；要求：尺规作图，保留作图痕迹
在的条件下，若，，求AC的长.
22.本小题9分
仔细阅读下面例题，解答问题：
例题：已知关于x的多项式有一个因式是，求另一个因式以及m的值．
解：设另一个因式为，得：，则，
，解得：，
另一个因式为，m的值为
问题：仿照以上方法解答下面问题：
二次三项式有一个因式是，求p的值；
已知关于x的多项式有一个因式是，求另一个因式以及k的值；
已知关于x的多项式有一个因式为，求b的值．
23.本小题10分
如图，已知中，，，，P，Q分别是的边上的两动点，点P从点B开始沿方向运动，速度为每秒1cm，到达A点后停止；点Q从A开始沿的方向运动，速度为每秒2cm，到达B点后停止，它们同时出发，设出发时间为
求BC的长度；
当t为何值时，点P恰好在边BC的垂直平分线上？并求出此时CQ的长；
当点Q在边BC上运动时，直接写出为等腰三角形时t的值.
答案和解析
1.【答案】C
【解析】【分析】
本题考查了对立方根的定义的理解和运用．
根据立方根的定义即可得出答案．
【解答】
解：因为，
所以8的立方根是2，
故选：
2.【答案】B
【解析】解：A、，不能构成直角三角形，不符合题意；
B、，能构成直角三角形，符合题意；
C、，不能构成直角三角形，不符合题意；
D、，不能构成直角三角形，不符合题意；
故选：
根据勾股定理的逆定理，逐个验证两短边长的平方和是否等于最长边的平方即可．
本题考查勾股定理的逆定理，解题的关键是掌握勾股定理的逆定理．
3.【答案】C
【解析】解：当时，，而，
说明命题“若，则”是假命题，
故选：
根据绝对值的性质、有理数的大小比较法则解答即可．
本题考查的是假命题的证明，任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．
4.【答案】A
【解析】解：A、，故A符合题意；
B、，故B不符合题意；
C、，故B不符合题意；
D、，故B不符合题意．
故选：
利用幂的乘方与积的乘方的法则，同底数幂的除法的法则，同底数幂的乘法的法则对各项进行运算即可．
本题主要考查同底数幂的除法，同底数幂的乘法，幂的乘方与积的乘方，解答的关键是对相应的运算法则的掌握．
5.【答案】D
【解析】【分析】
本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
要判定≌，已知，AC是公共边，具备了两组边对应相等，故添加、、后可分别根据SSS、SAS、HL能判定≌，而添加后则不能．
【解答】
解：添加，根据SSS，能判定≌，故A选项不符合题意；
B.添加，根据SAS，能判定≌，故B选项不符合题意；
C.添加，根据HL，能判定≌，故C选项不符合题意；
D.添加时，不能判定≌，故D选项符合题意；
故选：
6.【答案】D
【解析】解：
，
解得：，
故选：
首先根据多项式乘多项式法则进行运算，可得，，据此即可求得a、b的值，再代入代数式即可求得其值．
本题考查了多项式乘多项式法则，等式的定义，代数式求值问题，利用等式的定义求得a、b的值是解决问题关键．
7.【答案】A
【解析】解：当时，PN最短，
平分，于点M，，
最短
故选：
根据角平分线的性质及垂线段最短解答即可．
本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解题的关键．
8.【答案】D
【解析】解：根据图形可得：大正方形的面积为，阴影部分小正方形的面积为，一个小长方形的面积为xy，
则大正方形的面积-小正方形的面积个小长方形的面积，
即，
故选：
利用图形可得出大正方形的面积-小正方形的面积个小长方形的面积，写出大正方形的面积、阴影部分小正方形的面积和一个小长方形的面积即可得出答案
本题主要考查的是完全平方公式，解题关键是根据图形推出：大正方形的面积-小正方形的面积个小长方形的面积．
9.【答案】D
【解析】【分析】
根据线段垂直平分线的性质得出AD，AE当长，利用勾股定理逆定理得出是直角三角形，进而利用勾股定理解答即可．
本题考查了线段垂直平分线的性质和勾股定理的逆定理的应用，解题关键是是添加辅助线构造直角三角形．
【解答】
解：连接AD，AE，
的垂直平分线交BC于点D，AC的垂直平分线交BC于点E，
，，
，
，
是直角三角形，，
由勾股定理可得：，
故选
10.【答案】C
【解析】解：在中，由勾股定理得，
①，
在中，由勾股定理得，
，
点D、E分别是BC、AC的中点，
，，
②，
由①②可得负值已舍，负值已舍，
，
在中，由勾股定理得，
，
故选：
在与中，分别由勾股定理推出关于CE与CB的等式，从而求出CE与BC的长，在中，由勾股定理即可求出AB的长．
本题考查了勾股定理，熟练掌握勾股定理是解题的关键．
11.【答案】<
【解析】解：，
，
故答案为：
求出，根据即可求出答案．
本题考查了实数的大小比较的应用，关键是求出，题目比较典型，难度不大．
12.【答案】
【解析】解：，
在中，
故答案是：
这里首末两项是3和4y个数的平方，那么中间一项为加上或减去3x和4y乘积的2倍，故：
本题是完全平方公式的应用，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．注意积的2倍的符号，避免漏解．
13.【答案】
【解析】解：且，
故答案为：
根据等腰三角形的性质和三角形内角和得到
本题考查了等腰三角形的性质，熟练掌握等腰三角形的两个底角相等的性质是解题的关键．
14.【答案】9
【解析】解：由题意：，，
正方形A、C、D的面积依次为5、6、20，
，
故答案为：
根据勾股定理的几何意义：，解得即可．
本题考查了勾股定理，要熟悉勾股定理的几何意义，知道直角三角形两直角边的平方和等于斜边的平方．
15.【答案】25或16
【解析】解：在中，，，，
如图，作AB边上的高
，
①当为直角时，点P与点A重合，，
秒
②当为直角时，P与D重合，，，，
在中，，
，
解得
综上，当或16秒时，为直角三角形．
故答案为：25或
首先根据勾股定理求出斜边AB的长度，利用三角形的面积求出斜边上的高CD，再分两种情况进行讨论：①当为直角时，②当为直角时，分别求出此时的t值即可．
本题考查了勾股定理以及三角形的面积，解答本题的关键是掌握勾股定理的应用以及分情况讨论．
16.【答案】解：原式
；
原式
；
原式；
原式

【解析】先将立方根，绝对值化简，然后再进行计算即可解答；
先将绝对值，算术平方根化简，然后再进行计算即可解答；
利用提公因式法分解即可；
先提公因式，再利用完全平方公式分解即可．
本题主要考查了实数的混合运算，因式分解，熟练掌握各知识点是解答本题的关键．
17.【答案】解：原式
；
原式
；
，
当，时，原式
【解析】先计算同底数幂乘除法和积的乘方，再合并同类项即可；
根据多项式乘以多项式的计算法则求解即可；
先根据完全平方公式和平方差公式去中括号，再合并同类项，进一步根据多项式除以单项式的计算法则化简，最后代值计算即可．
本题主要考查了整式的混合计算，整式的化简求值，熟知整式的相关计算法则是解题的关键．
18.【答案】证明：中，，，，
又，
即，
是直角三角形；
证明：连接
是AB的垂直平分线，
，
设，则
解之得，即AE的长是
【解析】利用勾股定理逆定理：如果三角形的三边长a，b，c满足，那么这个三角形就是直角三角形可得是直角三角形；
根据线段垂直平分线的性质可得，设，则，根据勾股定理可得，再解即可．
此题主要考查了勾股定理逆定理和勾股定理，关键是掌握勾股定理的逆定理．
19.【答案】解：设长方形信封的长为3x cm，宽为2x cm，
由题意得，
，
，，
答：长方形信封的长为，宽为；
面积为的正方形贺卡的边长是16cm，
，
，
，即信封的宽大于正方形贺卡的边长，
小明能将这张贺卡不折叠就放入此信封．
【解析】设长方形信封的长为3x cm，宽为2x cm，由长方形的面积可求出x的值，从而求出长方形信封的长和宽；
先计算出正方形贺卡的边长，然后与长方形信封的宽进行比较，得出结论．
本题考查了算术平方根的应用，熟练掌握算术平方根的运算是解题的关键．
20.【答案】解：与互余，，
，，
，
在和中，
，
≌；
≌，，，
，，

【解析】根据互余的定义及直角三角形的性质推出，利用AAS即可证明≌；
根据全等三角形的性质及线段的和差求解即可．
此题考查了全等三角形的判定与性质，利用AAS证明≌是解题的关键．
21.【答案】解：如图：
过点D作，则
平分，
，
在和中，
，
，
在中，，
在中，设，
则，
，
解得：，
即：
【解析】根据“作角的平分线的基本作法”作图；
过点D作，垂足为E，则，接下来根据AAS可证和全等，进而可得，；在中，根据勾股定理求解BE的长，在中，设，则，根据勾股定理求解出AC的长．
本题考查了基本作图，掌握勾股定理的应用、全等三角形的判定和性质是解题的关键．，
22.【答案】解：设二次三项式的另一个因式为，则
，
即，
，
解得，
答：p的值为6；
设关于x的多项式另一个因式是，则
，
即，
，
解得，
关于x的多项式另一个因式是，；
设关于x的多项式另一个因式为，则
，
即，
，
解得，
答：
【解析】根据材料中提供的解法进行解答即可；
根据题意得出，进而得出方程组，求出方程组的解即可；
由题意可得，进而得出方程组，解这个方程组即可求出b的值．
本题考查列代数式、代数式求值，掌握多项式乘多项式的计算方法是解决问题的前提，根据多项式乘法的法则得出方程组是解决问题的关键．
23.【答案】解：，，
点P在边BC的垂直平分线上，取BC的中点D，作，交PA于BA，连接CP，
，，，
在中，，即
解得：
此时，此时Q走了；
，点Q在边BC上，
①当时，
秒．
②当时，
，
，
，
，
，
秒．
③当时，过A点作于点H，
，
，
秒．
综上所述：当t为6秒或秒或秒时，为等腰三角形．
【解析】由勾股定理即可得出结论；
可得，，则，解出可求出CQ；
用t分别表示出BQ和CQ，利用等腰三角形的性质可分、和三种情况，分别得到关于t的方程，可求得t的值．
本题考查了勾股定理、等腰三角形的性质、方程思想及分类讨论思想等知识．用时间t表示出相应线段的长，化“动”为“静”是解决这类问题的一般思路，注意方程思想的应用．