期中考试模拟试卷 2024—2025学年人教版数学九年级上册

这是一份期中考试模拟试卷 2024—2025学年人教版数学九年级上册，共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
考试时间：120分钟 满分：100分
一、单选题(共10题；共30分)
1．（3分）在同一坐标系中，作、、的图象，则它们（ ）
A．都是关于轴对称B．顶点都在原点
C．都是抛物线开口向上D．以上都不对
2．（3分）某班数学兴趣小组的同学互发微信，每两名同学都互相发一条．小明统计全组共互发了72次，设数学兴趣小组人数为x人，则可列方程为（ ）
A．B．C．D．
3．（3分）已知二次函数y＝（x-1）2+1，若点A（0，y1）和B（3，y2）在此函数图象上，则y1与y2的大小关系是（ ）
A．y1＞y2B．y1＜y2C．y1＝y2D．无法确定
4．（3分）如图，在正方形中，点E、F分别是边和上的点，若，为等边三角形，则（ ）
A．B．C．D．
5．（3分）如图，在中，，，分别为，的中点，将绕点顺时针旋转形成，连结．若，时，则为（ ）
A．B．C．D．
6．（3分）若关于的一元二次方程有两个不相等的实数根，则的取值范围是（ ）
A．B．C．D．
7．（3分）方程的解是（ ）
A．，B．，
C．，D．，
8．（3分）已知二次函数中，自变量x与函数y之间的部分对应值如下表：
在该函数的图象上有和两点，且，，与的大小关系正确的是（ ）
A．B．C．D．
9．（3分）如图，二次函数与x轴交于A，B两点，与y轴正半轴交于点C，它的对称轴为直线，则下列说法中正确的有（ ）
①；②；③；④；⑤方程其中一个解的取值范围为．
A．1个B．3个C．4个D．5个
10．（3分）如图，在△ABC中，AB＝AC＝4，∠BAC＝120°，P为BC边上一动点，连接AP，将线段AP绕点A顺时针旋转120°至AP′，则线段PP′的最小值为（ ）
A．B．C．D．
二、填空题(共8题；共24分)
11．（3分）方程的系数a，b，c满足，则方程有一个根为 ．
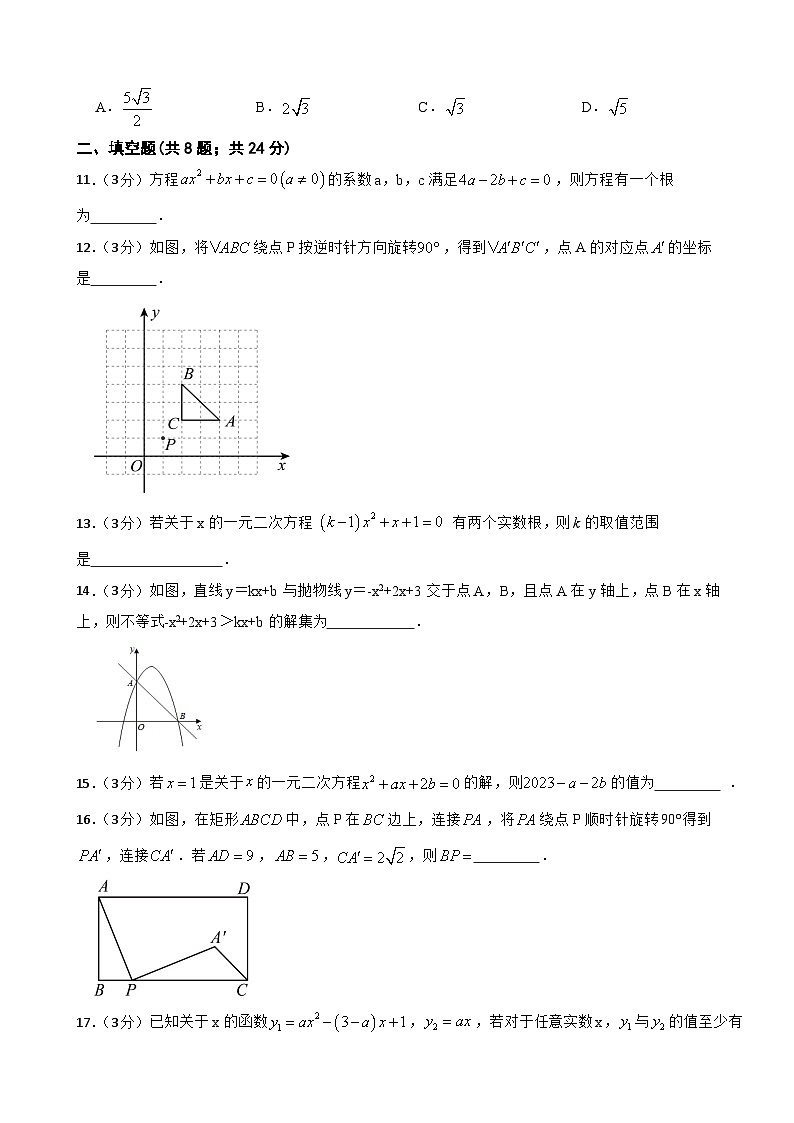
12．（3分）如图，将绕点P按逆时针方向旋转，得到，点A的对应点的坐标是 ．
13．（3分）若关于x的一元二次方程 有两个实数根，则k的取值范围是 ．
14．（3分）如图，直线y＝kx+b与抛物线y＝-x2+2x+3交于点A，B，且点A在y轴上，点B在x轴上，则不等式-x2+2x+3＞kx+b的解集为 ．
15．（3分）若是关于的一元二次方程的解，则的值为 ．
16．（3分）如图，在矩形中，点P在边上，连接，将绕点P顺时针旋转90°得到，连接．若，，，则 ．
17．（3分）已知关于x的函数，，若对于任意实数x，与的值至少有一个为正数．则实数a的取值范围是 ．
18．（3分）如图，正方形的边长为2，点在边上运动（不与点、重合），，点在射线上，且，与相交于点，连接、、．则下列结论：①；②；③；④面积的最大值为，其中正确结论的序号为 ．
三、解答题(共6题；共46分)
19．（7分）某电商销售某种商品一段时间后，发现该商品每天的销售量y（单位：千克）和每千克的售价x（单位：元）满足一次函数关系（如图所示），其中，
（1）求y关于x的函数解析式；
（2）若该种商品的成本为每千克40元，该电商如何定价才能使每天获得的利润最大？最大利润是多少？
20．（8分）二次函数的图象如图所示，根据图象解答下列问题：
（1）写出方程的两个根；
（2）若方程有两个不相等的实数根，求的取值范围；
（3）若抛物线与直线相交于，两点，写出抛物线在直线下方时的取值范围．
21．（8分）某商场在去年底以每件：80元的进价购进一批同型号的服装，一月份以每件150元的售价销售了320件，二、三月份该服装畅销，销量持续走高，在售价不变的情况下，三月底统计出三月份的销量达到了500件．
（1）（4分）求二、三月份服装销售量的平均月增长率；
（2）（4分）从四月份起商场因换季清仓采用降价促销的方式，经调查发现，在三月份销量的基础上，该服装售价每降价5元，月销售量增加10件，当每件降价多少元时，四月份可获利12000元？
22．（7分）若关于的方程x2-2m+1x+m2=0的有两个实数根，．
（1）求的取值范围；
（2）在（1）的条件下，若满足x1=x2，求实数的值．
23．（8分）小明对他击羽毛球的路线进行分析．如图，在平面直角坐标系中，点A，C在x轴上，球网与y轴的水平距离，，击球点P在y轴上．若小明选择扣球，羽毛球的飞行高度与水平距离近似满足一次函数关系；若小明选择吊球，羽毛球的飞行高度与水平距离近似满足二次函数关系．
（1）（2分）求点P的坐标和a的值；
（2）（3分）通过分析发现，上面两种击球方式均能使球过球网．要使球的落地点到点C的距离更近，请通过计算判断应选择哪种击球方式；
（3）（3分）小明在点P处再次以吊球的方式击球，此次羽毛球飞行路线的形状与的相同，且恰好落到点C处，则此次羽毛球飞行到最高点时与y轴的水平距离比 （填“大”或“小”）．
24．（8分）如图，已知抛物线经过，两点，与轴的另一个交点为．
（1）（2分）求抛物线的解析式；
（2）（3分）在抛物线对称轴上找一点，使得的值最小，直接写出点的坐标；
（3）（3分）设点为轴上的一个动点，是否存在使为等腰三角形的点，若存在，直接写出点的坐标；若不存在，说明理由．
答案解析部分
1．【答案】A
2．【答案】A
3．【答案】B
4．【答案】D
5．【答案】B
6．【答案】B
7．【答案】B
8．【答案】D
9．【答案】B
10．【答案】B
11．【答案】
12．【答案】
13．【答案】 且
14．【答案】0＜x＜3
15．【答案】
16．【答案】2
17．【答案】0＜a＜9
18．【答案】①②④
19．【答案】（1）y关于x的函数解析式为；（2）该电商定价为70元时才能使每天获得的利润最大，最大利润是1800元．
20．【答案】（1），；（2）；（3）或
21．【答案】（1）解：设二、三月份服装销售量的平均月增长率为，
依题意，得：，
解得：（不合题意，舍去）．
答：二、三月份服装销售量的平均月增长率为．
（2）解：设每件降价元，则四月份可售出件，
依题意，得：，
整理，得：，
解得：（不合题意，舍去）．
答：每件降价50元时，四月份可获利12000元．
22．【答案】（1）；（2）
23．【答案】（1）解：在一次函数，
令时，，
∴，
将代入中，可得：，
解得：；
（2）解：∵，，
∴，
选择扣球，则令，即：，解得：，
即：落地点距离点距离为，
∴落地点到C点的距离为，
选择吊球，则令，即：，
解得：（不合题意，舍去），
即：落地点距离点距离为，
∴落地点到C点的距离为，
∵，
∴选择吊球，使球的落地点到C点的距离更近．
（3）大
24．【答案】（1）解：把点，代入
得：，
解得：，
抛物线的解析式是；
（2）解：如图，1，易知：直线BC的解析式为，
抛物线的对称轴为直线，
直线BC与直线相交于点E，则，此时最小，
此时点E的坐标为；
（3）解：，，
，
，
分三种情况：
，如图，此时点的坐标为或；
当与重合时，也是等腰三角形，此时；
，如图，此时点的坐标为；
综上所述，点的坐标为或或或．x
…
0
1
2
3
…
y
…
－1
2
3
2
…