浙教版数学八上第一章 1.5. 2《用三边关系判定三角形全等 》 课件+教案+单元教案

这是一份浙教版数学八上第一章 1.5. 2《用三边关系判定三角形全等 》 课件+教案+单元教案，文件包含浙教版数学八上152《用两边夹角关系判定三角形全等》课件pptx、浙教版数学八上第1章《三角形的初步认识》单元整理分析教案docx、浙教版数学八上152《用两边夹角关系判定三角形全等》教案docx等3份课件配套教学资源，其中PPT共32页， 欢迎下载使用。

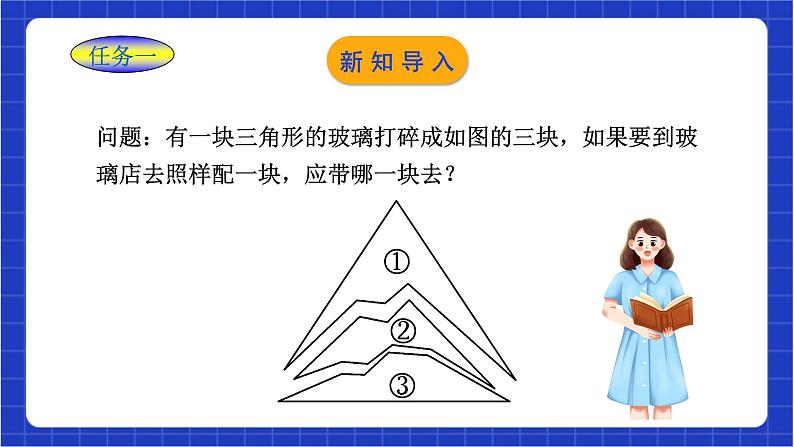
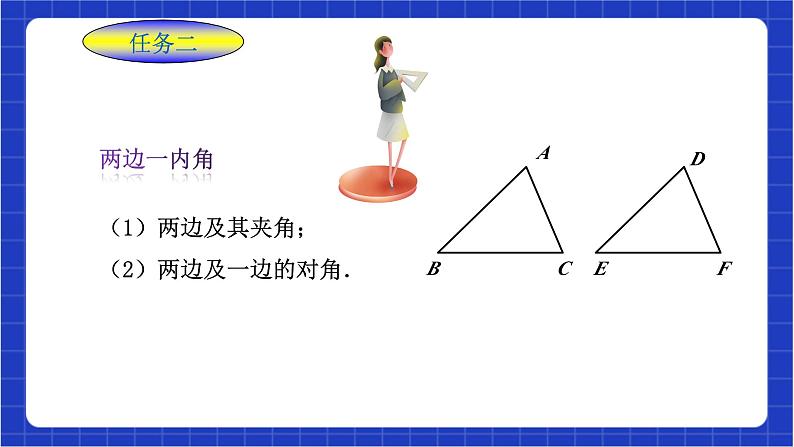
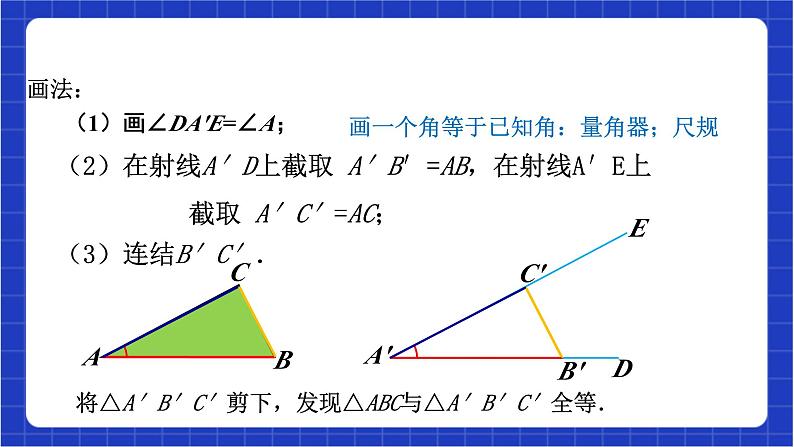
1.5.2 用两边夹角关系判定三角形全等 浙教版八年级上册教材分析 通过画图、比较、验证，培养学生注重观察、善于思考、严谨的思维习惯.经历探索三角形全等条件的过程，培养学生观察分析图形能力、动手能力.会运用三角形全等的判定方法、线段的中垂线的性质，解决两条线段相等、两个角相等的问题.教材分析教学目标教学目标：1.掌握三角形全等（SAS）的判定方法. 2.掌握线段垂直平分线的性质定理. 3.会运用三角形全等的判定方法、线段的中垂线的性质， 解决两条线段相等、两个角相等的问题.教学重点:两个三角形全等的判定条件（SAS）.教学难点:线段垂直平分线性质定理的证明涉及分类讨论.教学目标新知导入 任务一问题：有一块三角形的玻璃打碎成如图的三块，如果要到玻璃店去照样配一块，应带哪一块去？新知导入新知讲解　 三角形中只给一个条件或两个条件时，都不能保证所画出的三角形一定全等．给出三个条件时，有四种可能．你能说出是哪四种吗？（1）三内角（2）三条边（3）两边一内角（4）两内角一边SSS不能？？新知讲解 任务二（1）两边及其夹角；（2）两边及一边的对角．两边一内角ABCDEF 探究1：先任意画出一个△ABC，再画一个△A′B′C′，使A′B′＝AB，C′A′＝CA，∠A′=∠A（即保证两边和它们的夹角分别相等）.它们全等吗？（2）在射线A′D上截取 A′B′=AB，在射线A′E上 截取 A′C′=AC；A′B′C′画法：（3）连结B′C′．（1）画∠DA′E=∠A；ED将△A′B′C′剪下，发现△ABC与△A′B′C′全等．ABC画一个角等于已知角：量角器；尺规提炼概念 两边及其夹角分别相等的两个三角形全等．简称“边角边”和“SAS”．在△ABC与△DEF中，∴△ABC≌△DEF（SAS）．ABCDEF基 本 事 实：几何语言： 探究2：先任意画出一个△ABC，再画一个△A′B′C′，使A′B′＝AB，C′A′＝CA，∠B′=∠B（即保证两边和其中一边的对角分别相等）．它们全等吗？（3）以A′为圆心，以AC长为半径画弧，此时只要∠C≠90°，弧线一定和射线B′E交于两点C′，F．画法：（2）在射线B′D上截取B′A′=BA；（1）画∠DB′E=∠B；A′B′C′EDABCF所以SSA不能判定全等．而 △ABC与△ A′B′C′不全等．△ABC≌△ A′B′F ，典例精讲 【例】 已知：如图，AC与BD相交于点O，且OA=OC，OB=OD. 求证：△AOB≌△COD.垂直于一条线段，并且平分这条线段的直线叫做这条线段的垂直平分线，简称中垂线.【垂直平分线的定义】如图，直线l⊥AB于点D，且AD=BD，直线l就是线段AB的垂直平分线.【小组讨论】在直线l上任意取一点P，用圆规比较点P到点A，B的距离.你发现了什么？猜想：________________________________________________ 命题：线段垂直平分线上的点到线段两端的距离相等.由此你能得到什么结论？你能验证这一结论吗？点P1，P2，P3，… 到点A 与点B 的距离分别相等．证明 已知OA=OB，当点C与点O为同一点，即重合时，显然CA=CB.当点C与点O不重合时，∵直线l⊥AB(已知）∴∠COA=∠COB=90°(垂直的定义）.已知：如图，直线l⊥AB于点O，且OA=OB.C是直线l上的任意一点.求证：CA=CB.已知：如图，直线l⊥AB于点O，且OA=OB.C是直线l上的任意一点.求证：CA=CB.符号语言：∵　PC垂直平分AB(AC=BC,PC⊥AB)，∴　PA=PB．线段垂直平分线的性质线段垂直平分线上的点到线段两端的距离相等.归纳概念 由上面探究可知：（1）两边及夹角对应相等可以确定三角形的形状；（2）两边和其中一边的对角这三个条件无法唯一确定三角形的形状（即“边边角”对应相等或“SSA”），两个三角形不一定全等.课堂练习必做题1.如图，BD、AC交于O，若OA=OD，用“SAS”证△AOB≌△DOC还需（ ）A．AB=DC B．OB=OC C．∠A=∠D D．∠AOB=∠DOC B课堂练习2．如图，已知AB＝AC，AD＝AE，若要得到“△ABD≌△ACE”，必须添加一个条件，则下列所添条件不成立的是(　　)A．BD＝CE B．∠ABD＝∠ACEC．∠BAD＝∠CAE D．∠BAC＝∠DAEB选做题3.阅读下题及其证明过程：已知：如图，D是△ABC中BC边上一点，EB=EC，∠ABE=∠ACE求证：∠BAE=∠CAE证明：在△AEB和△AEC中，∴△AEB≌△AEC(第一步) ∴∠BAE=∠CAE(第二步) 问：上面证明过程是否正确？若正确，请写出每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程；EB=EC∠ABE=∠ACEAE=AE解：上面证明过程不正确；错在第一步，正确过程如下：在△BEC中，∵BE=CE∴∠EBC=∠ECB又∵∠ABE=∠ACE∴∠ABC=∠ACB∴AB=AC在△AEB和△AEC中，AE=AE，BE=CE，AB=AC∴△AEB≌△AEC（SSS）∴∠BAE=∠CAE.综合拓展题ABOCD4.如图,有一湖的湖岸在A、B之间呈一段圆弧状,A、B间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出A,B间的距离吗?作业布置1、如图，在△ABC中，∠ACB＝90°，D为AB的中点，DE⊥AB交AC于E，如果AC＝3 cm，BC＝1 cm，那么△BCE周长等于（ ）A．2 cm B．3 cm C．4 cm D．5 cmC作业布置选做题∵CD是线段AB的垂直平分线，∴CA=CB，DA=DB在△ABC与△ADC中∴△ABC≌△ADC∴ ∠DAC=∠DBC2. 如图，已知CD是线段AB的垂直平分线，则∠DAC=∠DBC吗？说明理由.解：AB=ADCB=CDAC=AC（ SSS）（全等三角形对应角相等）(垂直平分线的性质)(公共边)(已证)(已证)综合拓展题3．如图，△ABC，△CDE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点E在AB上．求证：△CDA≌△CEB.证明：∵△ABC，△CDE均为等腰直角三角形，∴BC＝AC，CE＝CD.∵∠ACB＝∠DCE＝90°，∴∠ACB－∠ACE＝∠DCE－∠ACE，即∠ECB＝∠DCA.课堂总结“SSA”不能判定两个三角形全等.课堂小结课堂总结作业布置教材课后配套作业题。 作业布置课程结束浙教版八年级上册