浙教版数学八上第一章 1.5. 4《用两角及其中一角的对边关系判定三角形全等》 课件+教案+单元教案

这是一份浙教版数学八上第一章 1.5. 4《用两角及其中一角的对边关系判定三角形全等》 课件+教案+单元教案，文件包含浙教版数学八上154《用两角及其中一角的对边关系判定三角形全等》课件pptx、浙教版数学八上第1章《三角形的初步认识》单元整理分析教案docx、浙教版数学八上154《用两角及其中一角的对边关系判定三角形全等》教案docx等3份课件配套教学资源，其中PPT共29页， 欢迎下载使用。

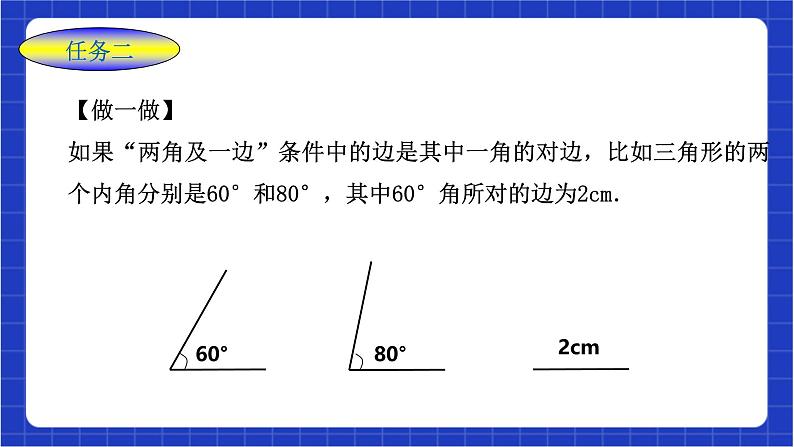
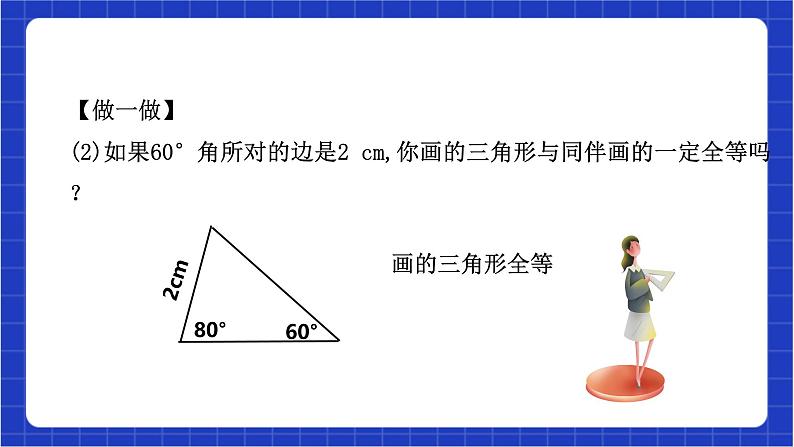
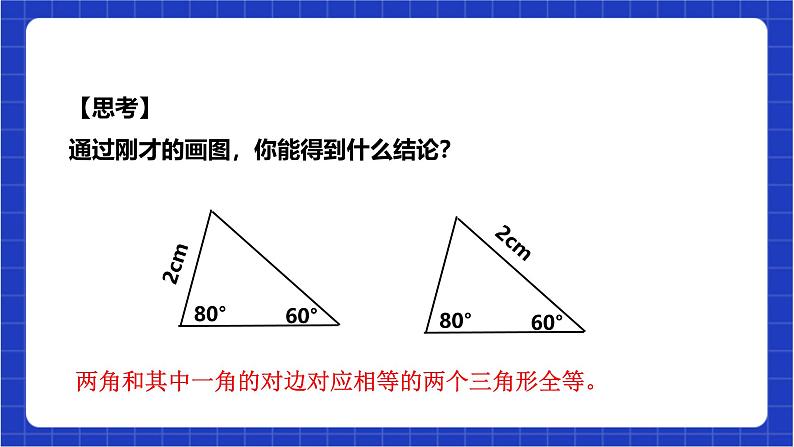
1.5.4 用两角及其中一角的对边关系判定三角形全等 浙教版八年级上册教材分析 在探索三角形全等条件及其运用的过程中，能够进行有条理的思考并进行简单推理. 学生对数学语言的理解还有待提高，如何判定两个三角形全等，需要老师积极引导．体会利用转化的数学思想和方法解决问题的过程.教材分析教学目标教学目标：1.探索并掌握两个三角形全等的条件：AAS； 2.会用AAS判定两个三角形全等； 3.理解角平分线的性质：角平分线上的点到角两边的距离 相等.教学重点:两个三角形全等的条件：两角及其中一个角的对边对应相等 的两个三角形全等．教学难点:例7需要添加辅助线，证明的思路较复杂，是本节教学的难 点．教学目标新知导入 任务一 到目前为止，我们已学过哪些方法判定两三角形全等？1. 全等三角形的定义能够完全重合的两个三角形全等三边对应相等的两个三角形全等2.边边边公理（SSS）3.边角边公理（SAS）两边及其夹角对应相等的两个三角形全等4.角边角公理（ASA）新知导入新知讲解议一议如果“两角及一边”条件中的边是其中一角的对边，情况会怎样呢？你能将它转化为“做一做”中的条件吗？新知讲解 任务二【做一做】如果“两角及一边”条件中的边是其中一角的对边，比如三角形的两个内角分别是60°和80°，其中60°角所对的边为2cm．2cm80°60°2cm80°60°画的三角形全等【做一做】(2)如果60°角所对的边是2 cm,你画的三角形与同伴画的一定全等吗？ 【思考】通过刚才的画图，你能得到什么结论？ 两角和其中一角的对边对应相等的两个三角形全等。在△ABC和△DEF中， ∠A=∠D, ∠B=∠E,BC=EF, △ABC和△DEF全等吗？为什么？ACBEDF分析：能否转化为ASA?证明：∵ ∠A=∠D, ∠B=∠E(已知) ∴∠C=∠F(三角形内角和定理) ∠B=∠E 在△ABC和△DEF中BC=EF ∠C=∠F∴△ABC≌△DEF（ASA）你能从上题中得到什么结论？两角及一角的对边对应相等的两个三角形全等提炼概念 有两角及一角的对边对应相等的两个三角形全等 （简写成“角角边”或“AAS”）判定三角形全等的定理4：数学语言表示：必须按照角角边的顺序书写能不能把“AAS”、“ASA”简述为“两角和一边对应相等的两个三角形全等”？　在△ADE和△ABC中但△ABC和△ADE不全等结论：说明两个三角形全等时,特别注意边和角“位置上对应相等”.例如：思考SSSSAS三角形全等的判定条件：（1）（2）ASAAAS三角形全等的判定条件：（3）（4）典例精讲 例6 已知：如图，点P是∠BAC的平分线上的一点，PB⊥AB于点P，PC⊥AC于点C.求证：PB=PC.∵ PB⊥AB,PC⊥AC∴∠ABP=∠ACP=90°在△APB与△APC中∴△APB≌△APC证明：∠PAB=∠PAC∠ABP=∠ACPAP=AP（ AAS）(已知)(公共边)(已证)(角平分线的定义)(垂线的定义)∴PB=PC（ 全等三角形对应边相等）角平分线上的点到角两边的距离相等.角平分线的性质定理：且PB⊥AB，PC⊥AC∴PB=PC（角平分线的性质）∵AP是∠BAC的角平分线几何语言（已知）归纳概念 角角边的情形包括：两角和其中一角的对边对应相等课堂练习必做题1.如图，给出下列四个条件，不能判断△ABC≌△A′B′C′的是（　　）①∠B=∠B′②∠C=∠C′③AC=A′C′④BC=B′C′． A．①②③ B．①②④ C．①③④ D．②③④A项，根据全等三角形的判定定理“AAS”，可推出两三角形全等，故本选项错误；B项，根据全等三角形的判定定理“ASA”，可推出两三角形全等，故本选项错误；C项，“SSA”不能推出两三角形全等，故本选项正确；D项，根据全等三角形的判定定理“SAS”，可推出两三角形全等，故本选项错误．C课堂练习2.如图∠ACB=∠DFE，BC=EF，请添加一个条件 ，（写出一个即可），能使△ABC≌△DEF∠B=∠E或∠A=∠D选做题3.如图，已知相交直线AB和CD，及另一直线MN，如果要在MN上找出与AB、CD距离相等的点，则这样的点至少有______个，最多有______个．21【解析】如图所示，分别作∠AOD及∠AOC的平分线OE与OF，∵OE与OF分别是∠AOD及∠AOC的平分线，∴直线OE与OF上的点到AB、CD距离相等，∴点M必在直线OE或直线OF上，∵点M在直线MN上，∴点M在这两条角平分线与直线MN的交点上，∴当OF或OE与MN平行时，符合条件的点有1个；当OF或OE均与直线MN不平行时，符合条件的点有2个．故答案为：1，2．综合拓展题 4.直角△ABC中，∠C＝90°，AD 平分∠CAB交BC于D，DE⊥AB于E，若AC＝6， BC＝8，AB＝10，CD＝3. (1)求DE的长；(2)求△ADB的面积． 解：(1)∵AD平分∠CAB，∴∠CAD＝∠EAD， ∵DE⊥AB，∠C＝90°，∴∠C＝∠DEA＝90°， 又∵AD为公共边，∴△ACD≌△AED， ∴CD＝DE，∵CD＝3，∴DE＝3； (2)∵AB＝10，DE＝3 ∴△ADB的面积为15．作业布置必做题1.如图，∠CAD=∠BAE，∠ACB=∠ADE，AB=AE，则可判定（　） A．△AEF≌△ABDB．△ABC≌△AEDC．△ADC≌△AFDD．以上答案都不对B作业布置选做题5 综合拓展题证明：过点N作NF⊥AB于F，NH⊥ED于H，NK⊥AC于K；过点M作MJ⊥BC于J，MP⊥AB于P，MQ⊥AC于Q．∵EN平分∠BED，DN平分∠EDC，∴NF=NH，NH=NK，∴NF=NK，∴N在∠A的平分线上．∵BM平分∠ABC，CM平分∠ACB∴MP=MJ，MQ=MJ，∴MP=MQ，∴M在∠A的平分线上．∵M、N都在∠A的平分线上，∴A、M、N在一条直线上．课堂总结判定条件全等三角形的定义SSSSASASAAAS边和角分别对应相等,而不是分别相等.两个三角形全等特别注意：关键：找符合要求的条件 课堂总结教材课后配套作业题。 作业布置课程结束浙教版八年级上册