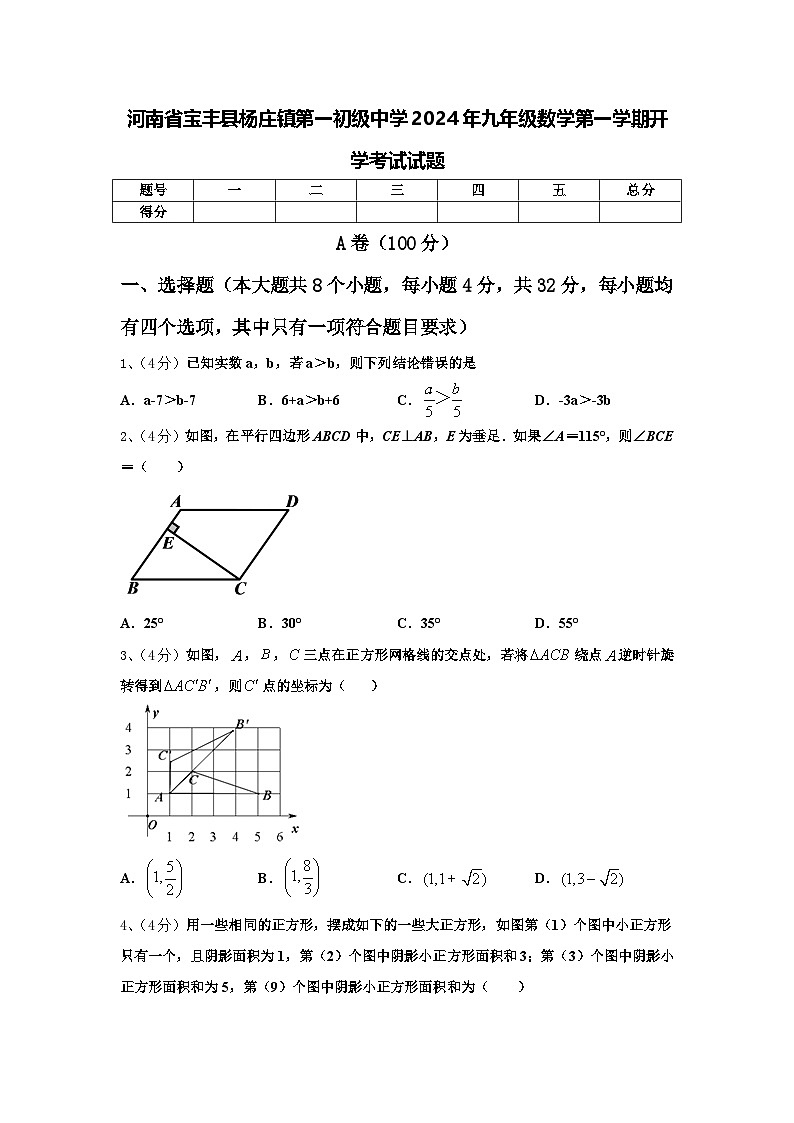
河南省宝丰县杨庄镇第一初级中学2024年九年级数学第一学期开学考试试题【含答案】

这是一份河南省宝丰县杨庄镇第一初级中学2024年九年级数学第一学期开学考试试题【含答案】，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知实数a，b，若a＞b，则下列结论错误的是
A．a-7＞b-7B．6+a＞b+6C．D．-3a＞-3b
2、（4分）如图，在平行四边形ABCD中，CE⊥AB，E为垂足．如果∠A＝115°，则∠BCE＝（ ）
A．25°B．30°C．35°D．55°
3、（4分）如图，，，三点在正方形网格线的交点处，若将绕点逆时针旋转得到，则点的坐标为（ ）
A．B．C．D．
4、（4分）用一些相同的正方形，摆成如下的一些大正方形，如图第（1）个图中小正方形只有一个，且阴影面积为1，第（2）个图中阴影小正方形面积和3；第（3）个图中阴影小正方形面积和为5，第（9）个图中阴影小正方形面积和为（ ）
A．11B．13C．15D．17
5、（4分）若把点A(－5m，2m－1)向上平移3个单位后得到的点在x轴上，则点A在( )
A．x轴上B．第三象限C．y轴上D．第四象限
6、（4分）下列函数中，正比例函数是（ ）
A．y＝B．y＝−C．y=x+4D．y=x2
7、（4分）教育局组织学生篮球赛，有x支球队参加，每两队赛一场时，共需安排45场比赛，则符合题意的方程为（ ）
A．B．C．D．
8、（4分）若一个多边形的内角和为外角和的3倍，则这个多边形为 （ ）
A．八边形B．九边形C．十边形D．十二边形
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）计算：＝_____．
10、（4分）如图，在平面直角坐标系中，点P（﹣1，2）关于直线x=1的对称点的坐标为_____．
11、（4分）如图，在△ABC中，AB=5，AC=7，BC=10，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，则PQ的长______．
12、（4分）若分式值为0，则的值为__________．
13、（4分）已知（﹣1，y1）（﹣2，y2）（， y3）都在反比例函数y=﹣的图象上，则y1 、y2 、 y3的大小关系是________ ．
三、解答题（本大题共5个小题，共48分）
14、（12分）在等边三角形ABC中，高AD＝m，求等边三角形ABC的面积．
15、（8分）如图，反比例函数y＝（k＞0）的图象与一次函数y＝x的图象交于A、B两点（点A在第一象限）．
（1）当点A的横坐标为4时．
①求k的值；
②根据反比例函数的图象，直接写出当﹣4＜x＜2（x≠0）时，y的取值范围；
（2）点C为y轴正半轴上一点，∠ACB＝90°，且△ACB的面积为10，求k的值．
16、（8分）某公司计划购买A、B两种计算器共100个，要求A种计算器数量不低于B种的，且不高于B种的．已知A、B两种计算器的单价分别是150元/个、100元/个，设购买A种计算器x个．
（1）求计划购买这两种计算器所需费用y（元）与x的函数关系式；
（2）问该公司按计划购买者两种计算器有多少种方案？
（3）由于市场行情波动，实际购买时，A种计算器单价下调了3m（m＞0）元/个，同时B种计算器单价上调了2m元/个，此时购买这两种计算器所需最少费用为12150元，求m的值．
17、（10分）如图，在平面直角坐标系中，四边形为平行四边形，为坐标原点，，将平行四边形绕点逆时针旋转得到平行四边形，点在的延长线上，点落在轴正半轴上．
(1)证明:是等边三角形:
(2)平行四边形绕点逆时针旋转度．的对应线段为,点的对应点为
①直线与轴交于点,若为等腰三角形，求点的坐标:
②对角线在旋转过程中设点坐标为，当点到轴的距离大于或等于时，求的范围．
18、（10分）如图，在△ABC中，AC=BC，∠C=36°，AD平分∠BAC交BC于点D．求证：AB=DC．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）将正比例函数国象向上平移个单位。则平移后所得图图像的解析式是_____.
20、（4分）如图，AB∥CD，∠B=68°，∠E=20°，则∠D的度数为 ．
21、（4分）直线的截距是__________．
22、（4分）如下图，将边长为 9cm 的正方形纸片 ABCD 折叠，使得点 A 落在边 CD 上的 E 点，折痕为 MN．若 CE 的长为 6cm，则 MN 的长为_____cm．
23、（4分）直线y=x+2与x轴的交点坐标为___________．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，网格中的图形是由五个小正方形组成的，根据下列要求画图（涂上阴影）．
（1）在图①中，添加一块小正方形，使之成为轴对称图形，且只有一条对称轴；（画一种情况即可）
（2）在图②中，添加一块小正方形，使之成为中心对称图形，但不是轴对称图形；
（3）在图③中，添加一块小正方形，使之成为既是中心对称图形又是轴对称图形．
25、（10分）如图，在□ABCD中，点E在AD上，请仅用无刻度直尺按要求作图（保留作图痕迹，不写作法）
（1）在图1中，过点E作直线EF将□ABCD分成两个全等的图形；
（2）在图2中，DE＝DC，请你作出∠BAD的平分线AM．
26、（12分）以四边形ABCD的边AB，AD为边分别向外侧作等边三角形ABF和等边三角形ADE，连接EB，FD，交点为G．
（1）当四边形ABCD为正方形时，如图①，EB和FD的数量关系是 ；
（2）当四边形ABCD为矩形时，如图②，EB和FD具有怎样的数量关系？请加以证明；
（3）如图③，四边形ABCD由正方形到矩形再到一般平行四边形的变化过程中，EB和FD具有怎样的数量关系？请直接写出结论，无需证明．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
A.∵a＞b，∴a-7＞b-7，∴选项A正确；
B.∵a＞b，∴6+a＞b+6，∴选项B正确；
C.∵a＞b，∴，∴选项C正确；
D.∵a＞b，∴-3a＜-3b，∴选项D错误.
故选D.
2、A
【解析】
由AD∥BC得到∠B=180°-∠A，而∠A=115°，由此可以求出∠B，又CE⊥AB，所以在三角形BCE中利用三角形内角和即可求出∠BCE．
【详解】
解：∵AD∥BC，
∴∠B=180°-∠A=65°，
又CE⊥AB，
∴∠BCE=90°-65°=25°．
故选：A．
此题主要考查平行四边形的性质和直角三角形的性质．
3、C
【解析】
根据旋转的性质可得AC=AC′，求出AC的长，得到C′的纵坐标，再根据点A的横坐标可得结果.
【详解】
解：如图，AC=，
由于旋转，
∴AC′=，
∵A（1，1），
∴C′（1，+1），
故选C.
本题考查了旋转的性质，解题的关键是根据旋转的性质得到AC=AC′.
4、D
【解析】
根据前4个图中阴影小正方形的面积和找到规律，然后利用规律即可解题．
【详解】
第（1）个面积为12﹣02＝1；
第（2）个面积为22﹣12＝3；
第（3）个面积为32﹣22＝5；
…
第（9）个面积为92﹣82＝17；
故选：D．
本题为图形规律类试题，找到规律是解题的关键．
5、D
【解析】
让点A的纵坐标加3后等于0，即可求得m的值，进而求得点A的横纵坐标，即可判断点A所在象限．
【详解】
∵把点A（﹣5m，2m﹣1）向上平移3个单位后得到的点在x轴上，∴2m﹣1+3＝0，解得：m＝﹣1，∴点A坐标为（5，﹣3），点A在第四象限．
故选D．
本题考查了点的平移、坐标轴上的点的坐标的特征、各个象限的点的坐标的符号特点等知识点，是一道小综合题．用到的知识点为：x轴上的点的纵坐标为0；上下平移只改变点的纵坐标．
6、B
【解析】
根据正比例函数、一次函数、反比例函数及二次函数的定义对各选项进行逐一分析即可．
【详解】
A、y=是反比例函数，故本选项错误；
B、y=-是正比例函数，故本选项正确；
C、y=x+4是一次函数，故本选项错误；
D、y=x2是二次函数，故本选项错误．
故选：B．
考查的是正比例函数的定义，熟知一般地，形如y=kx（k是常数，k≠0）的函数叫做正比例函数是解答此题的关键．
7、A
【解析】
先列出x支篮球队，每两队之间都比赛一场，共可以比赛x（x-1）场，再根据题意列出方程为．
【详解】
解：∵有x支球队参加篮球比赛，每两队之间都比赛一场，
∴共比赛场数为，
故选：A．
本题是由实际问题抽象出一元二次方程，主要考查了从实际问题中抽象出相等关系．
8、C
【解析】
设多边形的边数为n，而多边形的内角和公式为180（n-2)度，外角和为360度，则有：
180（n-2)=360×4，解方程可得．
【详解】
解：设多边形的边数为n,而多边形的内角和公式为180（n-2)度，外角和为360度，则有：
180（n-2)=360×4
n-2=8
解得：n=10
所以，这是个十边形
故选C．
本题考核知识点，多边形的内角和外角.解题关键点，熟记多边形内角和计算公式．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
分析：应用完全平方公式，求出算式的值是多少即可．
详解：=8﹣4+1=9﹣4．
故答案为9﹣4．
点睛：本题主要考查了二次根式的混合运算，要熟练掌握，解答此题的关键是要明确：①与有理数的混合运算一致，运算顺序先乘方再乘除，最后加减，有括号的先算括号里面的．②在运算中每个根式可以看做是一个“单项式”，多个不同类的二次根式的和可以看作“多项式”．
10、（3，2）
【解析】
对称点的纵坐标与点P的纵坐标相等，为2，
对称点与直线x=1的距离和P与直线x=1的距离相等，所以对称点的横坐标为3，
所以对称点的坐标为（3，2）.
点睛：掌握轴对称图形的性质.
11、1
【解析】
证明△ABQ≌△EBQ，根据全等三角形的性质得到BE=AB=5，AQ=QE，根据三角形中位线定理计算即可．
【详解】
解：在△ABQ和△EBQ中，
，
∴△ABQ≌△EBQ（ASA），
∴BE=AB=5，AQ=QE，
同理CD=AC=7，AP=PD，
∴DE=CD-CE=CD-（BC-BE）=2，
∵AP=PD，AQ=QE，
∴PQ=DE=1，
故答案为：1．
本题考查的是三角形中位线定理、全等三角形的判定和性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
12、-1
【解析】
根据分式值为0的条件进行求解即可.
【详解】
由题意得，x+1=0，
解得x=-1，
故答案为：-1.
本题考查了分式值为0的条件，熟练掌握分式值为0时，分子为0且分母不为0是解题的关键.
13、
【解析】
先根据反比例函数的解析式判断出函数图象所在的象限及其增减性，再由各点横坐标的值即可得出结论．
【详解】
∵反比例函数y=−2x中，k=−2