河南省三门峡市陕州区2024年九年级数学第一学期开学预测试题【含答案】

这是一份河南省三门峡市陕州区2024年九年级数学第一学期开学预测试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知直线y=2x-b经过点（1，-1），则b的值为( )
A．3B．-3C．0D．6
2、（4分）下列各组数据中能作为直角三角形的三边长的是（ ）
A．1，2，2B．C．13，14，15D．6，8，10
3、（4分）下列给出的四个点中，在直线的是（ ）
A．B．C．D．
4、（4分）若式子的值等于0，则x的值为（ ）
A．±2B．－2C．2D．－4
5、（4分）如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连结若，，则的度数为
A．B．C．D．
6、（4分）如图，平行四边形中，，，，动点从点出发，沿运动至点停止，设运动的路程为，的面积为，则与的函数关系用图象表示正确的是（ ）
A．B．
C．D．
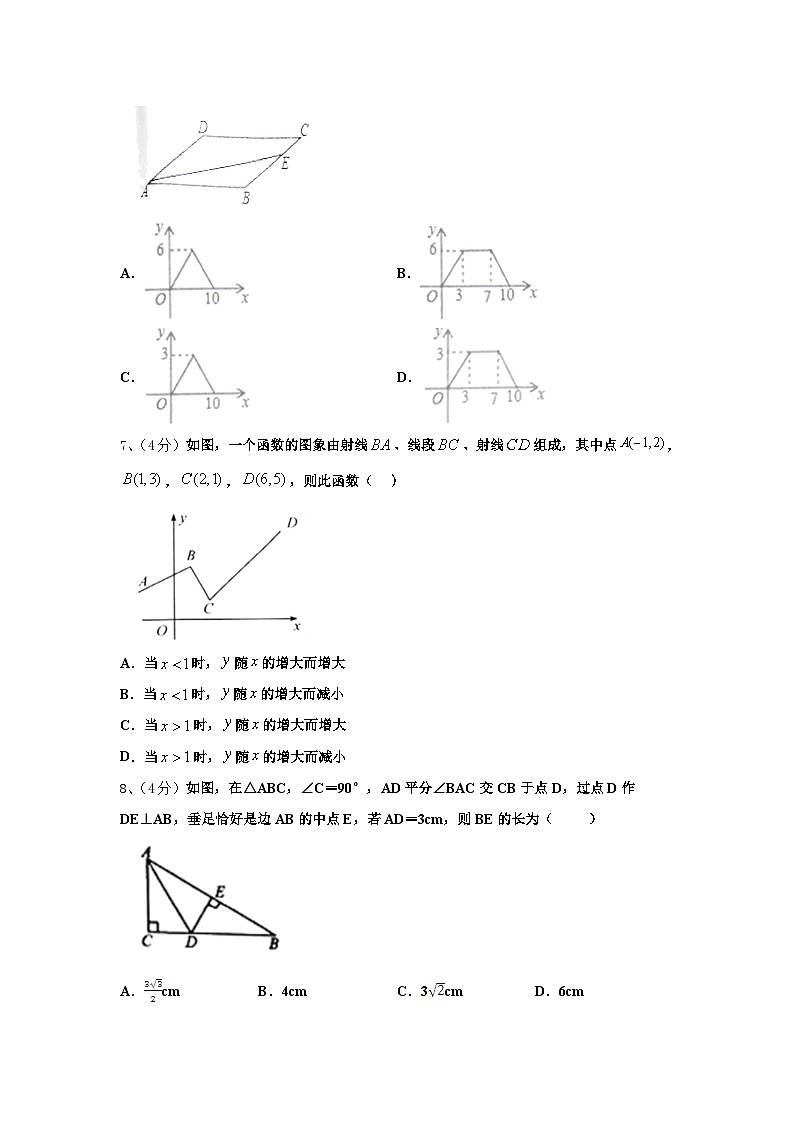
7、（4分）如图，一个函数的图象由射线、线段、射线组成，其中点，，，，则此函数（ ）
A．当时，随的增大而增大
B．当时，随的增大而减小
C．当时，随的增大而增大
D．当时，随的增大而减小
8、（4分）如图，在△ABC，∠C＝90°，AD平分∠BAC交CB于点D，过点D作DE⊥AB，垂足恰好是边AB的中点E，若AD＝3cm，则BE的长为（ ）
A．cmB．4cmC．3cmD．6cm
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）在一次“人与环境”知识竞赛中，共有25个题，每题四个答案，其中只有一个答案正确，每选对一题得4分，不选或选错倒扣2分，如果一个学生在本次竞赛中得分不低于60分，那么他至少要答对______题
10、（4分）若二次根式有意义，则x的取值范围是___．
11、（4分）观察下列各式：（x-1）（x+1）=x2-1；（x-1）（x2+x+1）=x3-1；（x-1）（x3+x2+x+1）=x4-1，根据前面各式的规律可得（x-1）（xn+xn-1+…+x+1）=______（其中n为正整数）．
12、（4分）已知点P(m-3,m+1)在第二象限，则m的取值范围是_______________.
13、（4分）在函数中，自变量x的取值范围是________________.
三、解答题（本大题共5个小题，共48分）
14、（12分）某校260名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵．将各类的人数绘制成扇形图（如图1）和条形图（如图2），经确认扇形图是正确的，而条形图尚有一处错误．
回答下列问题：
（1）写出条形图中存在的错误，并说明理由；
（2）写出这20名学生每人植树量的众数、中位数；
（3）在求这20名学生每人植树量的平均数时，小宇是这样分析的：
① 小宇的分析是从哪一步开始出现错误的？
② 请你帮他计算出正确的平均数，并估计这260名学生共植树多少棵．
15、（8分）解不等式组
16、（8分）如图，在正方形ABCD中，点E，F分别在边AD，CD上，
（1）若AB＝6，AE＝CF，点E为AD的中点，连接AE，BF．
①如图1，求证：BE＝BF＝3；
②如图2，连接AC，分别交AE，BF于M，M，连接DM，DN，求四边形BMDN的面积．
（2）如图3，过点D作DH⊥BE，垂足为H，连接CH，若∠DCH＝22.5°，则的值为 （直接写出结果）．
17、（10分）计算
（1）
（2）
（3）
18、（10分）如图，在矩形中，是上一点，垂直平分，分别交、、于点、、，连接、.
(1)求证：；
(2)求证：四边形是菱形；
(3)若，为的中点，，求的长.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）在直角坐标系中，直线与y轴交于点，按如图方式作正方形、、…，、、…在直线上，点、、…，在x轴上，图中阴影部分三角形的面积从左到右依次记为、、、..，则的值为________．
20、（4分）在湖的两侧有A，B两个观湖亭，为测定它们之间的距离，小明在岸上任选一点C，并量取了AC中点D和BC中点E之间的距离为50米，则A，B之间的距离应为______米．
21、（4分）不等式的负整数解有__________．
22、（4分）如图，依次连接第一个矩形各边的中点得到一个菱形，再依次连接菱形各边的中点得到第二个矩形，按照此方法继续下去．已知第一个矩形的面积为1，则第n个矩形的面积为_____．
23、（4分）如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为8 cm，正方形A的面积是10cm1，B的面积是11 cm1，C的面积是13 cm1，则D的面积为____cm1．
二、解答题（本大题共3个小题，共30分）
24、（8分）某校为了解学生每天参加户外活动的情况，随机抽查了100名学生每天参加户外活动的时间情况，并将抽查结果绘制成如图所示的扇形统计图．
请你根据图中提供的信息解答下列问题：
（1）请直接写出图中的值，并求出本次抽查中学生每天参加户外活动时间的中位数；
（2）求本次抽查中学生每天参加户外活动的平均时间．
25、（10分）如图，□ABCD中，在对角线BD上取E、F两点，使BE＝DF，连AE，CF，过点E作EN⊥FC交FC于点N，过点F作FM⊥AE交AE于点M；
（1）求证：△ABE≌△CDF；
（2）判断四边形ENFM的形状，并说明理由．
26、（12分）如图，在▱ABCD中，∠ABC的平分线交AD于点E，过点D作BE的平行线交BC于F．
（1）求证：△ABE≌△CDF；
（2）若AB=6，BC=8，求DE的长．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
将点（1，-1）代入y=2x-b，即可求解．
【详解】
解：将点（1，-1）代入y=2x-b得：
-1=2-b，解得：b=3，
故选：A．
本题考查的是一次函数点的坐标特征，将点的坐标代入函数表达式即可求解．
2、D
【解析】
根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形判定则可．
【详解】
解：A、，不能构成直角三角形，故不符合题意；
B、，不能构成直角三角形，故不符合题意；
C、，不能构成直角三角形，故不符合题意；
D、，能构成直角三角形，故符合题意．
故选：D．
本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．
3、D
【解析】
只需把每个点的横坐标即x的值分别代入，计算出对应的y值，然后与对应的纵坐标比较即可．
【详解】
解：A、当时，，则不在直线上；
B、当时，，则不在直线上；
C、当时，，则不在直线上；
D、当时，，则在直线上；
故选：D.
本题考查判断点是否在直线上，知识点是：在这条直线上的各点的坐标一定适合这条直线的解析式．
4、C
【解析】
=0且x²+4x+4≠0，
解得x=2.
故选C.
5、B
【解析】
【分析】直接利用三角形内角和定理得出的度数，再利用三角形中位线定理结合平行线的性质得出答案．
【详解】，，
，
▱ABCD的对角线AC与BD相交于点O，E是边CD的中点，
是的中位线，
，
，
故选B．
【点睛】本题主要考查了三角形内角和定理、三角形中位线定理等知识，得出EO是的中位线是解题关键．
6、D
【解析】
当点E在BC上运动时，三角形的面积不断增大，当点E在DC上运动时，三角形的面积不变，当点E在AD上运动时三角形的面积不等减小，然后计算出三角形的最大面积即可得出答案．
【详解】
当点E在BC上运动时,三角形的面积不断增大,最大面积= ×3××4=3；
当点E在DC上运动时，三角形的面积为定值3.
当点E在AD上运动时三角形的面不断减小，当点E与点A重合时，面积为0.
故选：D.
此题考查动点问题的函数图象，解题关键在于结合函数图象进行解答.
7、A
【解析】
根据一次函数的图象对各项分析判断即可.
【详解】
观察图象可知：
A. 当时，图象呈上升趋势，随的增大而增大，正确.
B. 当时，图象呈上升趋势，随的增大而减小, 故错误.
C. 当时，随的增大而减小,当时，随的增大而增大，故错误.
D. 当时，随的增大而减小,当时，随的增大而增大，故错误.
故选A.
考查一次函数的图象与性质，读懂图象是解题的关键.
8、A
【解析】
先根据角平分线的性质可证CD=DE，从而根据“HL”证明Rt△ACD≌Rt△AED，由DE为AB中线且DE⊥AB，可求AD=BD=3cm ，然后在Rt△BDE中，根据直角三角形的性质即可求出BE的长.
【详解】
∵AD平分∠BAC且∠C=90°，DE⊥AB，
∴CD=DE，
由AD＝AD，
所以，Rt△ACD≌Rt△AED，
所以，AC=AE.
∵E为AB中点，∴AC=AE=AB，
所以，∠B=30° .
∵DE为AB中线且DE⊥AB，
∴AD=BD=3cm ，
∴DE=BD=,
∴BE= cm.
故选A.
本题考查了角平分线的性质，线段垂直平分线的性质，全等三角形的判定与性质,含30°角的直角三角形的性质，及勾股定理等知识，熟练掌握全等三角形的判定与性质是解答本题的关键.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、19
【解析】
设他至少应选对x道题，则不选或错选为25−x道题．
依题意得4x−2(25−x)⩾60
得x⩾18
又∵x应为正整数且不能超过25
所以：他至少要答对19道题．故答案为19.
10、
【解析】
试题分析：根据题意，使二次根式有意义，即x﹣1≥0，解得x≥1．
故答案是x≥1．
考点：二次根式有意义的条件．
11、xn＋1－1
【解析】
观察其右边的结果：第一个是x2-1；第二个是x3-1；…依此类推，则第n个的结果即可求得．（x-1）（xn+xn-1+…x+1）=xn+1-1．
12、﹣1＜m＜1
【解析】
试题分析：让点P的横坐标小于0，纵坐标大于0列式求值即可．
解：∵点P（m﹣1，m+1）在第二象限，
∴m﹣1＜0，m+1＞0，
解得：﹣1＜m＜1．故填：﹣1＜m＜1．
【点评】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点．四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．
13、x≥0
【解析】
【分析】由已知可得，x≥0且x+1≠0,可求得x的取值范围.
【详解】由已知可得，x≥0且x+1≠0,
所以，x的取值范围是x≥0
故答案为：x≥0
【点睛】本题考核知识点：自变量取值范围.解题关键点：根据式子的特殊性求自变量的取值范围.
三、解答题（本大题共5个小题，共48分）
14、解：（1）D错误
（2）众数为1，中位数为1．
（2）①小宇的分析是从第二步开始出现错误的．
②1278（颗）
【解析】
分析：（1）条形统计图中D的人数错误，应为20×10%．
（2）根据条形统计图及扇形统计图得出众数与中位数即可．
（2）①小宇的分析是从第二步开始出现错误的；
②求出正确的平均数，乘以260即可得到结果．
解：（1）D错误，理由为：
∵共随机抽查了20名学生每人的植树量，由扇形图知D占10%，
∴D的人数为20×10%=2≠2．
（2）众数为1，中位数为1．
（2）①小宇的分析是从第二步开始出现错误的．
②（棵）．
估计260名学生共植树1.2×260=1278（颗）
15、﹣1≤x＜2
【解析】
首先分别计算出两个不等式的解集，再根据“大小小大中间找”找出公共解集即可．
【详解】
解不等式①，得：x＜2，
解不等式②，得：x≥﹣1，
所以不等式组的解集为﹣1≤x＜2，
将不等式组的解集表示在数轴上如下：
此题主要考查了一元一次不等式组的解法，关键是掌握解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
16、（1）①详见解析；②12；（2）.
【解析】
（1）①先求出AE＝3，进而求出BE，再判断出△BAE≌△BCF，即可得出结论；
②先求出BD＝6，再判断出△AEM∽△CMB，进而求出AM＝2，再判断出四边形BMDN是菱形，即可得出结论；
（2）先判断出∠DBH＝22.5°，再构造等腰直角三角形，设出DH，进而得出HG，BG，即可得出BH，结论得证．
【详解】
解：（1）①∵四边形ABCD是正方形，
∴AB＝BC＝AD＝6，∠BAD＝∠BCD＝90°，
∵点E是中点，
∴AE＝AD＝3，
在Rt△ABE中，根据勾股定理得，BE＝＝3，
在△BAE和△BCF中，
∴△BAE≌△BCF（SAS），
∴BE＝BF，
∴BE＝BF＝3；
②如图2，连接BD，
在Rt△ABC中，AC＝AB＝6，
∴BD＝6，
∵四边形ABCD是正方形，
∴AD∥BC，
∴△AEM∽△CMB，
∴，
∴，
∴AM＝AC＝2，
同理：CN＝2，
∴MN＝AC﹣AM﹣CN＝2，
由①知，△ABE≌△CBF，
∴∠ABE＝∠CBF，
∵AB＝BC，∠BAM＝∠BCN＝45°，
∴△ABM≌△CBN，
∴BM＝BN，
∵AC是正方形ABCD的对角线，
∴AB＝AD，∠BAM＝∠DAM＝45°，
∵AM＝AM，
∴△BAM≌△DAM，
∴BM＝DM，
同理：BN＝DN，
∴BM＝DM＝DN＝BN，
∴四边形BMDN是菱形，
∴S四边形BMDN＝BD×MN＝×6×2＝12；
（2）如图3，设DH＝a，
连接BD，
∵四边形ABCD是正方形，
∴∠BCD＝90°，
∵DH⊥BH，
∴∠BHD＝90°，
∴点B，C，D，H四点共圆，
∴∠DBH＝∠DCH＝22.5°，
在BH上取一点G，使BG＝DG，
∴∠DGH＝2∠DBH＝45°，
∴∠HDG＝45°＝∠HGD，
∴HG＝HD＝a，
在Rt△DHG中，DG＝HD＝a，
∴BG＝a，
∴BH＝BG+HG＝A+A＝（+1）a，
∴．
故答案为．
此题是四边形综合题，主要考查了正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质，菱形的判定和性质，勾股定理，判断出四边形BMDN是菱形是解本题的关键．
17、（1）（2）（3）
【解析】
（1）先把各二次根式化为最简二次根式，然后去括号后合并即可；
（2）利用二次根式的乘除法则运算，然后合并同类二次根式即可；
（3）根据平方差公式和完全平方公式进行计算．
【详解】
（1）
解：原式


（2）
解：原式

（3）
解：原式

本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．
18、 (1)证明见解析；(2)证明见解析；(3).
【解析】
（1）先根据线段垂直平分线的性质证明PB＝PE，由ASA证明△BOQ≌△EOP；
（2）由（1）得出PE＝QB，证出四边形BPEQ是平行四边形，再根据菱形的判定即可得出结论；
（3）根据三角形中位线的性质可得AE＋BE＝2OF＋2OB＝18，设AE＝x，则BE＝18−x，在Rt△ABE中，根据勾股定理可得，BE＝10，得到，设PE＝y，则AP＝8−y，BP＝PE＝y，在Rt△ABP中，根据勾股定理可得，解得，在Rt△BOP中，根据勾股定理可得，由PQ＝2PO即可求解．
【详解】
解：(1)∵垂直平分，
∴，，
∵四边形是矩形，
∴，
∴，
在与中，，
∴，
(2)∵
∴，
又∵，
∴四边形是平行四边形，
又∵，
∴四边形是菱形；
(3)∵，分别为，的中点，
∴，
设，则，在中，，
解得，，
∴，
设，则，，
在中，，
解得，
在中，，
∴.
本题考查了菱形的判定与性质、矩形的性质，平行四边形的判定与性质、线段垂直平分线的性质、勾股定理等知识；本题综合性强，有一定难度．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
根据=，=，找出规律从而得解.
【详解】
解：
∵直线，当x=0时，y=1，当y=0时，x=﹣1，
∴OA1=1，OD=1，
∴∠ODA1=45°，
∴∠A2A1B1=45°，
∴A2B1=A1B1=1，
∴=，
∵A2B1=A1B1=1，
∴A2C1=2=，
∴=，
同理得：A3C2=4=，…，=，
∴=，
故答案为．
20、1
【解析】
根据三角形中位线的性质定理，解答即可．
【详解】
∵点D、E分别为AC、BC的中点，
∴AB=2DE=1（米），
故答案为：1．
本题主要考查三角形中位线的性质定理，掌握三角形的中位线平行于第三边，且等于第三边长的一半，是解题的关键．
21、-5、-4、-3、-2、-1
【解析】
求出不等式的解集，取解集范围内的负整数即可.
【详解】
解：移项得：
合并同类项得：
系数化为1得：
即
所以原不等式的负整数解为：-5、-4、-3、-2、-1
故答案为：-5、-4、-3、-2、-1
本题主要考查了求不等式的整数解，确定不等式的解集是解题的关键.
22、（）n-1
【解析】
试题分析：已知第一个矩形的面积为1；
第二个矩形的面积为原来的（）2-1=；
第三个矩形的面积是（）3-1=；
…
故第n个矩形的面积为：．
考点：1.矩形的性质；2.菱形的性质．
23、30
【解析】
根据正方形的面积公式，运用勾股定理可得结论：四个小正方形的面积之和等于最大的正方形的面积64 cm1，问题即得解决.
【详解】
解：如图记图中三个正方形分别为P、Q、M.
根据勾股定理得到：A与B的面积的和是P的面积；C与D的面积的和是Q的面积；而P、Q的面积的和是M的面积.
即A、B、C、D的面积之和为M的面积.
∵M的面积是81=64，
∴A、B、C、D的面积之和为64，设正方形D的面积为x，
∴11+10+13+x=64，
∴x=30，
故答案为30.
本题主要考查勾股定理，把正方形的面积转化为相关直角三角形的边长，再通过勾股定理探索图形面积的关系是解决此类问题常见的思路.
二、解答题（本大题共3个小题，共30分）
24、（1）a=20%．本次抽查中学生每天参加活动时间的中位数是1；
（2）本次抽查中学生每天参加户外活动的平均时间是1.175小时．
【解析】
（1）用1减去其它组的百分比即可求得a的值，然后求得各组的人数，根据中位数定义求得中位数；
（2）利用加权平均数公式即可求解．
【详解】
解：（1）a=1﹣15%﹣25%﹣40%=20%．
100×20%=20（人），
100×40%=40（人），
100×25%=25（人），
100×15%=15（人）．
则本次抽查中学生每天参加活动时间的中位数是1；
（2）=1.175（小时）．
答：本次抽查中学生每天参加户外活动的平均时间是1.175小时．
考点：1.扇形统计图；2.加权平均数；3.中位数．
25、（1）见解析；（2）四边形ENFM是矩形．见解析.
【解析】
（1）根据SAS即可证明；
（2）只要证明三个角是直角即可解决问题；
【详解】
（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AB＝CD
∴∠ABD＝∠CDB，又∵BE＝DF，
∴△ABE≌△CDF（SAS）．
（2）由（1）得，∴∠AEB＝∠CFD，
∴∠AED＝∠CFB，
∴AE∥CF
又∵EN⊥CF，∠AEN＝∠ENF＝90°，
又∵FM⊥AE，∠FME＝90°，
∴四边形ENFM是矩形．
本题考查平行四边形的性质、全等三角形的判定和性质、矩形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
26、（1）证明见解析（2）2
【解析】
（1）首先由平行四边形的性质可得AD∥BC，AB=CD；∠A=∠C，再由条件利用SAS定理可判定△ABE≌△CDF；（2）由(1)可知 ∠EBF=∠AEB由平行线的性质和角平分线得出∠AEB=∠ABE，即可得出结果.
解：（1）证明：法一：
∵四边形ABCD是平行四边形
∴AD∥BC，AD=BC，∠A=∠C，,
∵BE∥DF，
∴四边形BEDF是平行四边形，
∴DE=BF，
∴AD-DE=BC-BF，
即：AE=CF，
∴△ABE≌△CDF（SAS）.
法二：∵BE//FD ∴∠EBF=∠DFC
∵AD//BC ∴∠EBF=∠AEB
∴∠AEB=∠DFC
在▱ABCD中，∵∠A=∠C，AB=CD
∴ △ABE≌△CDF
（2）由(1)可知 ∠EBF=∠AEB
又∵BE平分∠EBF
∴∠EBF=∠ABE
∴∠AEB=∠ABE
∴AE=AB=6
又∵BC=AD=8
∴DE=2
“点睛”本题考查了平行四边形的判定与性质、等腰三角形的判定；熟记平行四边形的性质，证出AE=AB是解决（2）的关键.
题号
一
二
三
四
五
总分
得分