黑龙江省红光农场学校2025届数学九年级第一学期开学质量检测试题【含答案】

这是一份黑龙江省红光农场学校2025届数学九年级第一学期开学质量检测试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）在2014年的体育中考中，某校6名学生的体育成绩统计如图，则这组数据的众数、中位数、方差依次是( )
A．18，18，1B．18，17.5，3C．18，18，3D．18，17.5，1
2、（4分）下列计算正确的是（ ）
A．＝﹣3B．C．5×5＝5D．
3、（4分）下列调查：
（1）为了检测一批电视机的使用寿命；
（2）为了调查全国平均几人拥有一部手机；
（3）为了解本班学生的平均上网时间；
（4）为了解中央电视台春节联欢晚会的收视率．
其中适合用抽样调查的个数有（ ）
A．1个B．2个C．3个D．4个
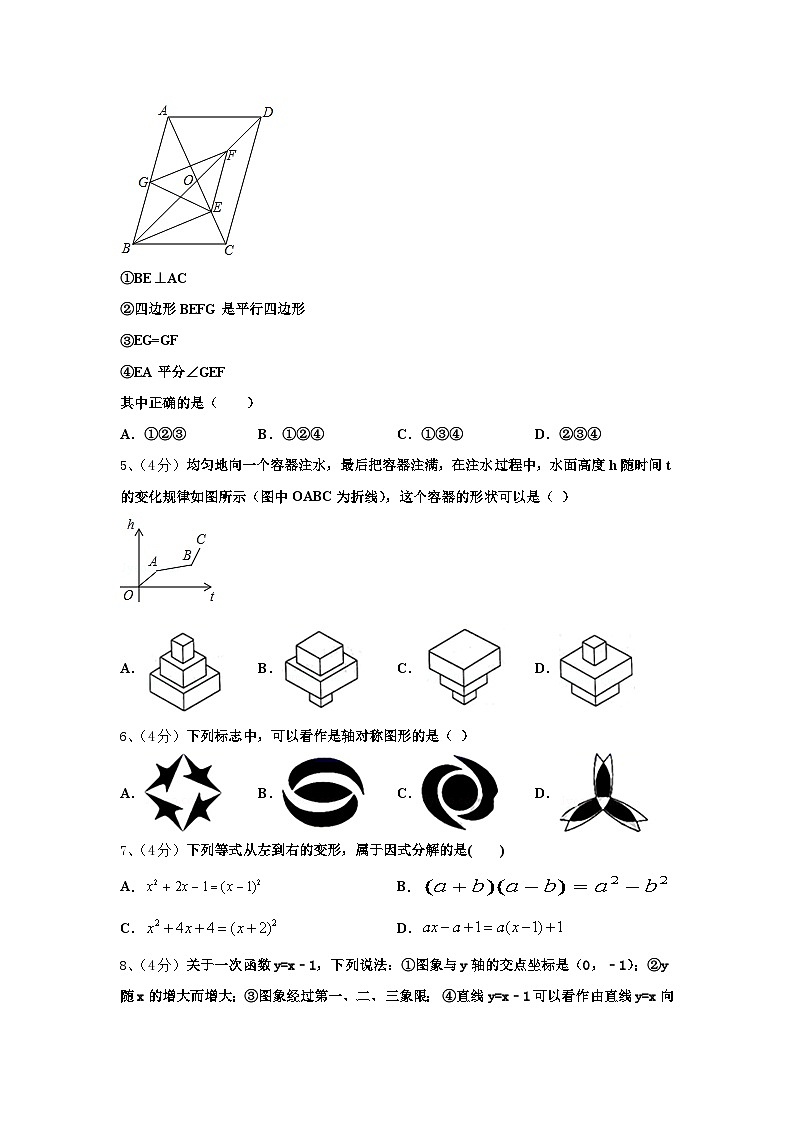
4、（4分）如图，▱ABCD中，对角线AC，BD相交于O，BD=2AD，E，F，G分别是OC，OD，AB的中点，下列结论
①BE⊥AC
②四边形BEFG是平行四边形
③EG=GF
④EA平分∠GEF
其中正确的是（ ）
A．①②③B．①②④C．①③④D．②③④
5、（4分）均匀地向一个容器注水，最后把容器注满，在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为折线），这个容器的形状可以是（ ）
A．B．C．D．
6、（4分）下列标志中，可以看作是轴对称图形的是（ ）
A．B．C．D．
7、（4分）下列等式从左到右的变形，属于因式分解的是( )
A．B．
C．D．
8、（4分）关于一次函数y=x﹣1，下列说法：①图象与y轴的交点坐标是（0，﹣1）；②y随x的增大而增大；③图象经过第一、二、三象限； ④直线y=x﹣1可以看作由直线y=x向右平移1个单位得到．其中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）化简:=_________.
10、（4分）分解因式：_____.
11、（4分）某种感冒病毒的直径是0.000 000 12米，用科学记数法表示为 米．
12、（4分）如图，在矩形ABCD中，AB=6cm，BC=8cm，现将其沿EF对折，使得点C与点A重合，点D落在处，AF的长为___________．
13、（4分）如图，正方形OABC的边OA，OC在坐标轴上，矩形CDEF的边CD在CB上，且5CD=3CB，边CF在轴上，且CF=2OC-3，反比例函数y= (k>0)的图象经过点B,E，则点E的坐标是____
三、解答题（本大题共5个小题，共48分）
14、（12分）如图（1），在矩形中，分别是的中点，作射线，连接.
（1）请直接写出线段与的数量关系；
（2）将矩形变为平行四边形，其中为锐角，如图（2），，分别是的中点，过点作交射线于点，交射线于点，连接，求证：；
（3）写出与的数量关系，并证明你的结论.
15、（8分）先阅读下列材料，再解答下列问题：
材料：因式分解：(x＋y)2＋2(x＋y)＋1.
解：将“x＋y”看成整体，令x＋y＝A，则
原式＝A2＋2A＋1＝(A＋1)2.
再将“A”还原，得原式＝(x＋y＋1)2.
上述解题用到的是“整体思想”，“整体思想”是数学解题中常用的一种思想方法，请你解答下列问题：
(1)因式分解：1＋2(x－y)＋(x－y)2＝_______________；
(2)因式分解：(a＋b)(a＋b－4)＋4；
(3)求证：若n为正整数，则式子(n＋1)(n＋2)(n2＋3n)＋1的值一定是某一个整数的平方．
16、（8分）如图，是边长为2的等边三角形，将沿直线平移到的位置，连接．
（1）求平移的距离；
（2）求的长．
17、（10分）观察下面的变形规律：，
解答下面的问题：
（1）若为正整数，请你猜想 ；
（2）计算：.
18、（10分）如图,在中, 是的中点,连接并延长交的延长线于点.
（1）求证：；
（2）若，，求的度数.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）当x________时，分式有意义.
20、（4分）若恒成立，则A+B＝____．
21、（4分）计算-=_______.
22、（4分）已知点P（3﹣m，m）在第二象限，则m的取值范围是____________________．
23、（4分）如图，长方形ABCD的边AB在x轴上，且AB的中点与原点重合，，，直线与矩形ABCD的边有公共点，则实数b的取值范围是________．
二、解答题（本大题共3个小题，共30分）
24、（8分）计算：÷
25、（10分）如图，将一矩形纸片OABC放在平面直角坐标系中，，，．动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动，运动秒时，动点P从点A出发以相同的速度沿AO向终点O运动．当其中一点到达终点时，另一点也停止运动．设点P的运动时间为t（秒）．
（1）OP =____________, OQ =____________；（用含t的代数式表示）
（2）当时，将△OPQ沿PQ翻折，点O恰好落在CB边上的点D处．
①求点D的坐标；
②如果直线y = kx + b与直线AD平行，那么当直线y = kx + b与四边形PABD有交点时，求b 的取值范围．
26、（12分）瑞安市文化创意实践学校是一所负责全市中小学生素质教育综合实践活动的公益类事业单位，学校目前可开出：创意手工创意表演、科技制作（创客）、文化传承、户外拓展等5个类别20多个项目课程．
（1）学校3月份接待学生1000人，5月份增长到2560人，求该学校接待学生人数的平均月增长率是多少？
（2）在参加“创意手工”体验课程后，小明发动本校同学将制作的作品义卖募捐．当作品卖出的单价是2元时，每天义卖的数量是150件；当作品的单价每涨高1元时，每天义卖的数量将减少10件．问：在作品单价尽可能便宜的前提下，当单价定为多少元时，义卖所得的金额为600元？
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
根据众数、中位数的定义和方差公式分别进行解答即可．
【详解】
这组数据18出现的次数最多，出现了3次，则这组数据的众数是18；
把这组数据从小到大排列，最中间两个数的平均数是（18+18）÷2=18，则中位数是18；
这组数据的平均数是：（17×2+18×3+20）÷6=18，则方差是：[2×（17﹣18）2+3×（18﹣18）2+（20﹣18）2]=1．
故选A．
本题考查了众数、中位数和方差，众数是一组数据中出现次数最多的数；中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；一般地设n个数据，x1，x2，…xn的平均数为，则方差S2[（x1）2+（x2）2+…+（xn）2]．
2、D
【解析】
根据二次根式的性质对A进行判断；根据二次根式的加减运算对B进行判断；根据二次根式的乘法法则对C进行判断；根据二次根式的除法法则对D进行判断．
【详解】
A、原式＝3，所以A选项错误；
B、与不能合并，所以B选项错误；
C、原式＝25，所以C选项错误；
D、原式＝＝2，所以D选项正确．
故选D．
本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后合并同类二次根式即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
3、C
【解析】
试题分析：根据对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查可分析出答案．
解：（1）为了检测一批电视机的使用寿命适用抽样调查；
（2）为了调查全国平均几人拥有一部手机适用抽样调查；
（3）为了解本班学生的平均上网时间适用全面调查；
（4）为了解中央电视台春节联欢晚会的收视率适用抽样调查；
故选C．
4、B
【解析】
由平行四边形的性质可得OB=BC，由等腰三角形的性质可判断①正确，由直角三角形的性质和三角形中位线定理可判断③错误，由BG=EF，BG∥EF∥CD可证四边形BEFG是平行四边形，可得②正确．由平行线的性质和等腰三角形的性质可判断④正确．
【详解】
∵四边形ABCD是平行四边形，
∴BO=DO=BD，AD=BC，AB=CD，AB∥BC，
又∵BD=2AD，
∴OB=BC=OD=DA，且点E 是OC中点，
∴BE⊥AC，
故①正确，
∵E、F分别是OC、OD的中点，
∴EF∥CD，EF=CD，
∵点G是Rt△ABE斜边AB上的中点，
∴GE=AB=AG=BG，
∴EG=EF=AG=BG，无法证明GE=GF，
故③错误，
∵BG=EF，BG∥EF∥CD，
∴四边形BEFG是平行四边形，
故②正确，
∵EF∥CD∥AB，
∴∠BAC=∠ACD=∠AEF，
∵AG=GE，
∴∠GAE=∠AEG，
∴∠AEG=∠AEF，
∴AE平分∠GEF，故④正确，
故选B．
本题考查了菱形的判定，平行四边形的性质，全等三角形的判定和性质，三角形中位线定理等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．
5、D
【解析】
试题分析：注水量一定，函数图象的走势是稍陡，平，陡；那么速度就相应的变化，跟所给容器的粗细有关．则相应的排列顺序就为D．故选D．
考点：函数的图象．
6、D
【解析】
根据轴对称图形与中心对称图形的概念求解．
【详解】
解：A、不是轴对称图形，是中心对称图形，不符合题意；
B、不是轴对称图形，是中心对称图形，不符合题意；
C、不是轴对称图形，是中心对称图形，不符合题意；
D、是轴对称图形，符合题意．
故选D．
本题考查了中心对称图形和轴对称图形的定义，掌握中心对称图形与轴对称图形的概念，解答时要注意：判断轴对称图形的关键是寻找对称轴，图形两部沿对称轴叠后可重合；判断中心对称图形是要寻找对称中心，图形旋转180度后与原图重合．
7、C
【解析】
根据因式分解的意义，把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解分别进行判断，即可得出答案．
【详解】
解：A、x2+2x-1≠（x-1）2，故本选项错误；
B、右边不是整式积的形式，不是因式分解，故本选项错误；
C、符合因式分解的定义，故本选项正确；
D、右边不是整式积的形式，不是因式分解，故本选项错误．
故选：C．
本题考查多项式的因式分解，解题的关键是正确理解因式分解的意义．
8、C
【解析】
①将x=0代入一次函数解析式中求出y值，由此可得出结论①符合题意；②由k=1＞0结合一次函数的性质即可得出y随x的增大而增大，即结论②符合题意；③由k、b的正负结合一次函数图象与系数的关系即可得出该函数图象经过第一、三、四象限，即结论③不符合题意；④根据平移“左加右减”即可得出将直线y=x向右平移1个单位得到的直线解析式为y=x-1，即结论④符合题意．综上即可得出结论．
【详解】
①当x=0时，y=-1，
∴图象与y轴的交点坐标是（0，-1），结论①符合题意；
②∵k=1＞0，
∴y随x的增大而增大，结论②符合题意；
③∵k=1＞0，b=-1＜0，
∴该函数图象经过第一、三、四象限，结论③不符合题意；
④将直线y=x向右平移1个单位得到的直线解析式为y=x-1，
∴结论④符合题意．
故选：C．
考查了一次函数的性质、一次函数图象与系数的关系以及一次函数图象与几何变换，逐一分析四条结论是否符合题意是解题的关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
根据三角形法则计算即可解决问题．
【详解】
解：原式=，
= ，
= ，
=.
故答案为.
本题考查平面向量、三角形法则等知识，解题的关键是灵活运用三角形法则解决问题，属于中考基础题．
10、
【解析】
直接提取公因式a即可得答案.
【详解】
3a2+a=a(3a+1)，
故答案为：a(3a+1)
本题考查提取公因式法分解因式，正确找出公因式是解题关键.
11、
【解析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．0.00000012=.
12、
【解析】
根据对折之后对应边长度相同，联立直角三角形中勾股定理即可求解．
【详解】
设
∵矩形纸片中，，
现将其沿对折，使得点C与点A重合，点D落在处，
∴ ，
在中，，
即 解得 ，
故答案为：．
本题考查了矩形的性质和勾股定理的应用，解题的关键在于找到对折之后对应边相等关系和勾股定理中的等量关系．
13、
【解析】
设正方形OABC的边0A=a，可知OA=OC=AB=CB=a，所以点B的坐标为(aa)，推出反比例函数解析式的k=a，再由CF=2OC-3，可知CF=2a-3，推出点的坐标为( ,3a-3)，根据5CD=3CB，可求出点E的坐标
【详解】
由题意可设：正方形OABC的边OA=a
∴OA= OC=AB= CB
∴点B的坐标为(a,a)，即k=a
CF=2OC-3
∴CF=2a-3
∵OF=OC+CF=a+2a-3=3a-3
∴点E的纵坐标为3a-3
将3a-3代入反比例函数解析式y= 中,可得点E的横坐标为
∵四边形CDEF为矩形,
∴CD=EF=
5CD=3CB
=3a,可求得:a=
将a=,代入点E的坐标为( ,3a-3),
可得:E的坐标为
故答案为：
本题考查了反比例函数图像上点的坐标特征,正方形矩形的性质,熟知在反比例函数的题目中利用设点法找等量关系解方程是解题关键
三、解答题（本大题共5个小题，共48分）
14、（1）MD＝MC；（2）见解析；（3）∠BME＝3∠AEM，证明见解析.
【解析】
（1）由“SAS”可证△ADM≌△BCM，可得MD＝MC；
（2）由题意可证四边形ADNM是平行四边形，可得AD∥MN，可得EF＝FC，MF⊥EC，由线段垂直平分线的性质可得ME＝MC；
（3）由等腰三角形的性质和平行线的性质可得∠BME＝3∠AEM．
【详解】
解：（1）∵四边形ABCD是矩形，
∴AD＝BC，∠A＝∠B＝90°，
∵点M是AB中点，
∴AM＝BM，
∴△ADM≌△BCM（SAS），
∴MD＝MC；
（2）∵M、N分别是AB、CD的中点，
∴AM＝BM，CN＝DN，
∵四边形ABCD是平行四边形，
∴AB＝CD，AB∥CD，
∴DN＝AM＝CN＝BM，
∴四边形ADNM是平行四边形，
∴AD∥MN，
∴，∠AEC＝∠NFC＝90°，
∴EF＝CF，且MF⊥EC，
∴ME＝MC；
（3）∠BME＝3∠AEM，
证明：∵EM＝MC，EF＝FC，
∴∠EMF＝∠FMC，
∵AB＝2BC，M是AB中点，
∴MB＝BC，
∴∠BMC＝∠BCM，
∵MN∥AD，AD∥BC，
∴AD∥MN∥BC，
∴∠AEM＝∠EMF，∠FMC＝∠BCM，
∴∠AEM＝∠EMF＝∠FMC＝∠BCM＝∠BMC，
∴∠BME＝3∠AEM.
本题是四边形综合题，考查了平行四边形的判定和性质，矩形的性质，全等三角形的判定和性质，等腰三角形的性质等知识，（2）中证明EF＝CF是本题的关键．
15、 (1)(x－y＋1)2；（2）见解析；（3）见解析.
【解析】
分析：（1）把（x-y）看作一个整体，直接利用完全平方公式因式分解即可；(2)令A=a+b,带入后因式分解即可将原式因式分解；(3)将原式转化为(n²+3n) [(n+1)（n+2）]+1,进一步整理为(n²+3n+1) ²,根据n为正整数，从而说明原式是整数的平方.
本题解析：
(1).1+2(x-y)+(x+y) ²=（x﹣y+1）2；
（2）令A=a+b，则原式变为A（A﹣4）+4=A2﹣4A+4=（A﹣2）2，
故（a+b）（a+b﹣4）+4=（a+b﹣2）2；
（3）（n+1）（n+2）（n2+3n）+1=（n2+3n）[（n+1）（n+2）]+1
=（n2+3n）（n2+3n+2）+1
=（n2+3n）2+2（n2+3n）+1
=（n2+3n+1）2，
∵n为正整数，
∴n2+3n+1也为正整数，
∴代数式（n+1）（n+2）（n2+3n）+1的值一定是某一个整数的平方．
点睛;本题考查了因式分解的应用，解题的关键是认真审题你，理解题意，掌握整体思想解决问题.
16、（1）2；（2）
【解析】
（1）由平移的性质，即可得出平移距离；
（2）由平移的性质以及边长关系，可判定∠BAE=90°，利用勾股定理即可得解.
【详解】
（1）∵△DCE由△ABC平移而成
∴△ABC的平移距离为BC=2；
（2）由平移，得
BE=2BC=4，AB=AC=CE
∵等边△ABC
∴∠BAC=∠ACB=60°
∴∠CAE=∠CEA=30°
∴∠BAE=∠BAC+∠CAE=60°+30°=90°
∴.
此题主要考查等边三角形、平移的性质以及勾股定理的运用，熟练掌握，即可解题.
17、（1）；（2）.
【解析】
（1）根据所给算式写出结论即可；
（2）根据（1）中规律把括号内变形，然后合并同类二次根式，再根据平方差公式计算.
【详解】
解：（1）∵，，，，
∴；
原式
.
本题考查了二次根式的混合运算，根据所给算式总结出是解答本题的关键.
18、（1）详见解析；（2）35°.
【解析】
（1）欲证明AE=FE，只要证明△ADE≌△FCE（AAS）即可．
（2）根据∠DAE=∠BAD-∠FAB，只要求出∠BAD，∠FAB即可．
【详解】
解：（1）证明：∵四边形是平行四边形，是的中点，
∴，，
∴，， ，
∴≌（），
∴．
（2）∵四边形是平行四边形，
∴，由（1）的结论知，
∴，
∵，
∴，
∴
∴，
∴∠BAD=180°−∠B=70°，
∴∠DAE=∠BAD−∠FAB=70°−35°=35°.
此题考查平行四边形的性质，全等三角形的判定与性质，解题关键在于证明△ADE≌△FCE.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
根据分母不等于0列式求解即可．
【详解】
由题意得，x−1≠0，
解得x≠1.
故答案为：≠1.
本题考查分式有意义的条件，熟练掌握分式的基本性质是解题关键.
20、2.
【解析】
根据异分母分式加减法法则将进行变形，继而由原等式恒成立得到关于A、B的方程组，解方程组即可得.
【详解】
，
又∵
∴，
解得，
∴A+B＝2，
故答案为：2.
本题考查了分式的加减法，恒等式的性质，解二元一次方程组，得到关于A、B的方程组是解题的关键.
21、2
【解析】
利用二次根式的减法法则计算即可.
【详解】
解：原式
故答案为：
本题考查二次根式的减法运算，熟练掌握二次根式的减法运算法则是解题关键.
22、m>3.
【解析】
试题分析：因为点P在第二象限，所以，，解得：
考点：（1）平面直角坐标；（2）解不等式组
23、−1≤b≤1
【解析】
由AB，AD的长度可得出点A，C的坐标，分别求出直线经过点A，C时b的值，结合图象即可得出结论．
【详解】
解：∵AB＝1，AD＝1，
∴点A的坐标为（−1，0），点C的坐标为（1，1）．
当直线y＝−x＋b过点A时，0＝1＋b，
解得：b＝−1；
当直线y＝−x＋b过点C时，1＝−1＋b，
解得：b＝1．
∴当直线y＝−x＋b与矩形ABCD的边有公共点时，实数b的取值范围是：−1≤b≤1．
故答案为：−1≤b≤1．
本题考查了一次函数图象上点的坐标特征以及矩形的性质，利用极限值法求出直线经过点A，C时b的值是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、-1．
【解析】
直接利用二次根式的混合运算法则分别化简得出答案．
【详解】
解：原式
．
此题主要考查了二次根式的混合运算，熟悉运算法则是解题关键．
25、（1）6-t； t+（2）①D(1，3) ②3≤b≤
【解析】
（1）根据OA的长以及点P运动的时间与速度可表示出OP的长，根据Q点的运动时间以及速度即可得OQ的长；
（2）①根据翻折的性质结合勾股定理求得CD长即可得；
②先求出直线AD的解析式，然后根据直线y=kx+b与直线AD平行，确定出k=，从而得表达式为：，根据直线与四边形PABD有交点，把点P、点B坐标分别代入求出b即可得b的取值范围.
【详解】
（1）由题意可知AP=t，所以OP=OA-AP=6-t，
根据Q点运动秒时，动点P出发，所以OQ＝t+，
故答案为6-t， t+；
（2）①当t=1时，OQ=，
∵C(0，3)，
∴OC=3，
∴CQ=OC-OQ=，
∵△OPQ沿PQ翻折得到△DPQ，
∴QD = OQ =，
在Rt△CQD中，有CD2=DQ2-CQ2，所以CD=1，
∵四边形OABC是矩形，
∴D(1，3)；
②设直线AD的表达式为：（m≠0），
∵点A（6，0），点D（1，3），
∴，
解得，
∴直线AD的表达式为：，
∵直线y=kx+b与直线AD平行，
∴k=，
∴表达式为：，
∵直线与四边形PABD有交点，
∴当过点P（5，0）时，解得：b=3，
∴当过点B（6，3）时，解得：b=，
∴3≤b≤.
本题考查了矩形的性质、折叠的性质、勾股定理、一次函数的应用等，综合性较强，有一定的难度，熟练掌握相关性质与定理以及待定系数法是解题的关键.
26、（1）该学校接待学生人数的增长率为60%；（2）单价定为5元．
【解析】
（1）设平均月增长率为，根据题意得到一元二次方程即可求解；
（2）设定价为元，求出可卖出的件数，根据义卖所得的金额为600元得到一元二次方程即可求解．
【详解】
解：（1）设平均月增长率为，则根据题意得，
解得，（舍），
∴该学校接待学生人数的增长率为60%．
（2）设定价为元，此时可卖出件，
∴可列方程，解得，．
∵作品单价要尽可能便宜，
∴单价定为5元．
答：当单价定为5元时，义卖所得的金额为600元．
本题考查了一元二次方程的应用，关键在于明确数量与每件利润的表示方法．
题号
一
二
三
四
五
总分
得分
批阅人