湖北省武汉市武昌区省水二中学2024年九上数学开学达标检测模拟试题【含答案】

这是一份湖北省武汉市武昌区省水二中学2024年九上数学开学达标检测模拟试题【含答案】，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）若x＜2，化简＋|3－x|的正确结果是( )
A．－1B．1C．2x－5D．5－2x
2、（4分）在以x为自变量， y为函数的关系式y=5πx中，常量为（ ）
A．5B．πC．5πD．πx
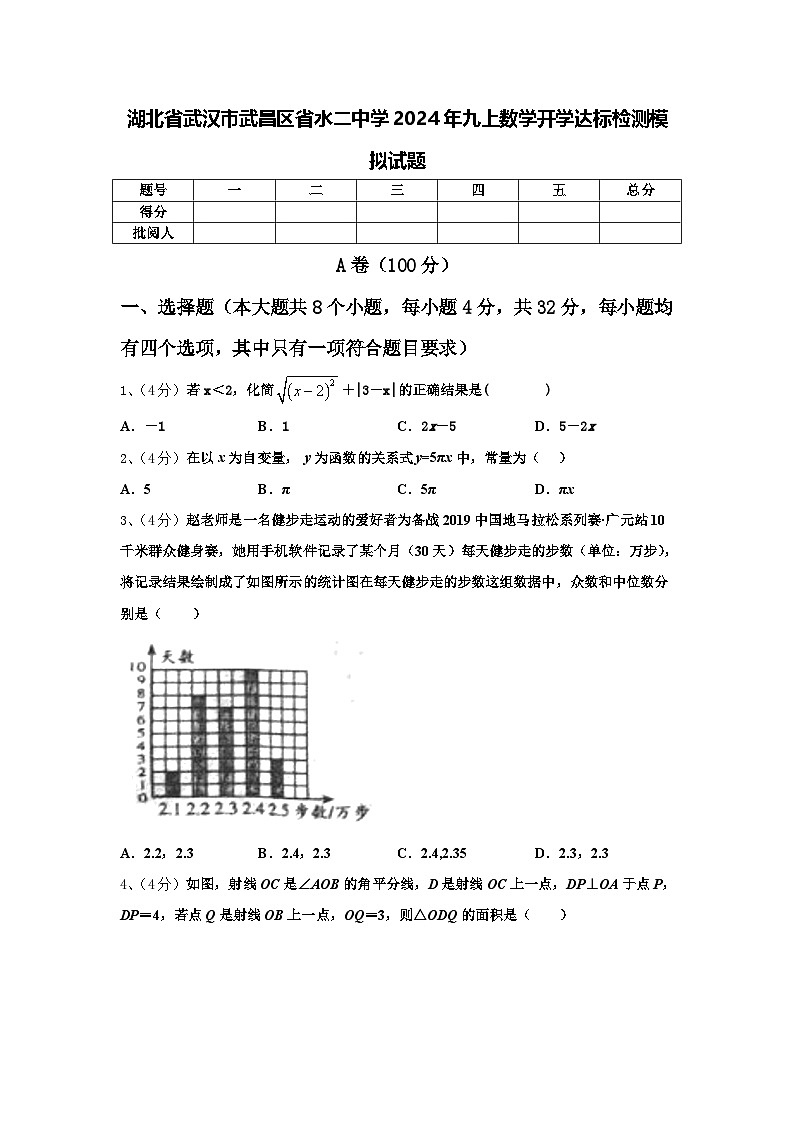
3、（4分）赵老师是一名健步走运动的爱好者为备战2019中国地马拉松系列赛·广元站10千米群众健身赛，她用手机软件记录了某个月（30天）每天健步走的步数（单位：万步），将记录结果绘制成了如图所示的统计图在每天健步走的步数这组数据中，众数和中位数分别是（ ）
A．2.2，2.3B．2.4，2.3C．2.4,2.35D．2.3，2.3
4、（4分）如图，射线OC是∠AOB的角平分线，D是射线OC上一点，DP⊥OA于点P，DP＝4，若点Q是射线OB上一点，OQ＝3，则△ODQ的面积是（ ）
A．3B．4
C．5D．6
5、（4分）将直线y＝kx－1向上平移2个单位长度，可得直线的解析式为（ ）
A．y＝kx＋1 B．y＝kx－3 C．y＝kx＋3 D．y＝kx－1
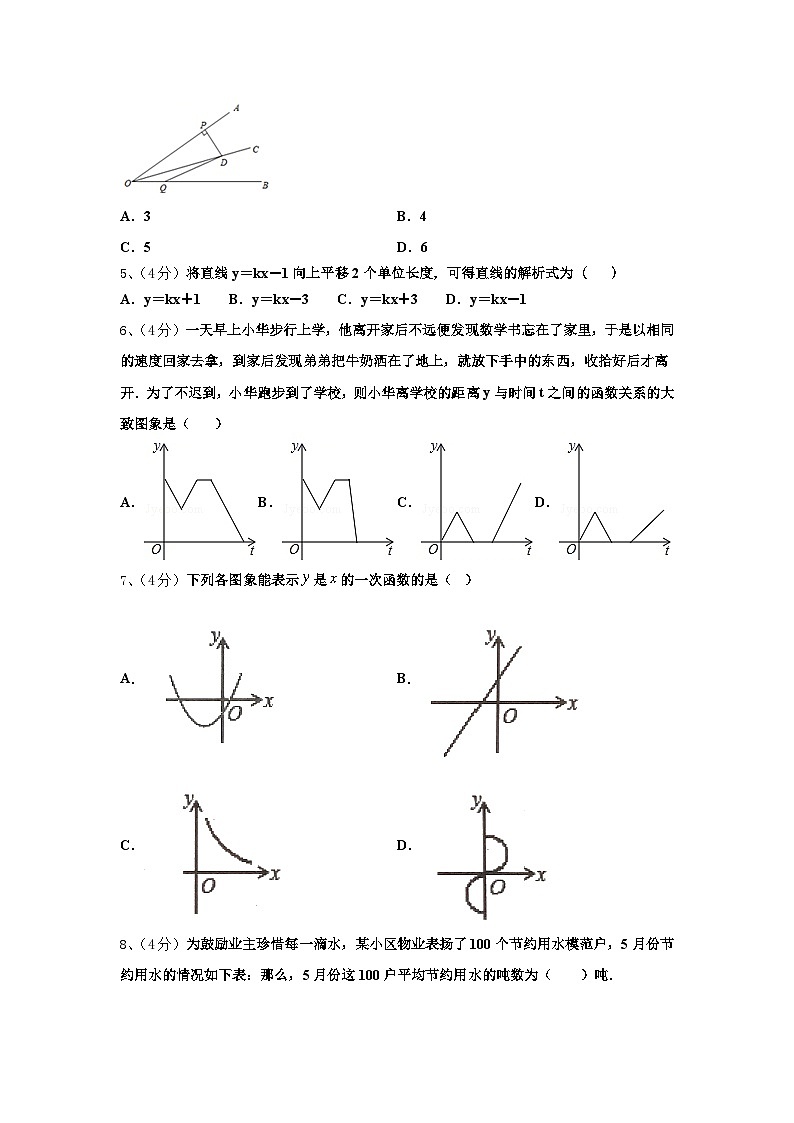
6、（4分）一天早上小华步行上学，他离开家后不远便发现数学书忘在了家里，于是以相同的速度回家去拿，到家后发现弟弟把牛奶洒在了地上，就放下手中的东西，收拾好后才离开．为了不迟到，小华跑步到了学校，则小华离学校的距离y与时间t之间的函数关系的大致图象是（ ）
A．B．C．D．
7、（4分）下列各图象能表示是的一次函数的是（ ）
A．B．
C．D．
8、（4分）为鼓励业主珍惜每一滴水，某小区物业表扬了100个节约用水模范户，5月份节约用水的情况如下表：那么，5月份这100户平均节约用水的吨数为（ ）吨．
A．1B．1.1C．1.13D．1.2
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）为响应“低碳生活”的号召，李明决定每天骑自行车上学，有一天李明骑了1000米后，自行车发生了故障，修车耽误了5分钟，车修好后李明继续骑行，用了8分钟骑行了剩余的800米，到达学校（假设在骑车过程中匀速行驶）．若设他从家开始去学校的时间为t（分钟），离家的路程为y（千米），则y与t（15＜t≤23）的函数关系为________．
10、（4分）如图是某超市一层到二层电梯的示意图，其中AB、CD分别表示超市一层、二层电梯口处地面的水平线，∠ABC＝150°，BC的长约为12米，则乘电梯从点B到点C上升的高度h约为________米．
11、（4分）若关于x的一元二次方程x2﹣2x+4m=0有实数根，则m的取值范围是_____．
12、（4分）在△ABC ，∠BAC  90, AB  AC  4, O 是 BC 的中点， D 是腰 AB 上一动点，把△DOB 沿 OD 折叠得到 △DOB' ，当 ∠ADB'  45 时， BD 的长度为_____.
13、（4分）某校为了解学生最喜欢的球类运动情况，随机选取该校部分学生进行调查，要求每名学生只写一类最喜欢的球类运动．以下是根据调查结果绘制的统计图表的一部分．
那么，其中最喜欢足球的学生数占被调查总人数的百分比为______%．
三、解答题（本大题共5个小题，共48分）
14、（12分）已知一次函数的图象经过点A（0，﹣2），B（3，4），C（5，m）．
求：（1）这个一次函数的解析式；
（2）m的值．
15、（8分）如图，在菱形ABCD中，AD∥x轴，点A的坐标为(0，4)，点B的坐标为(3，0)．CD边所在直线y1＝mx＋n与x轴交于点C，与双曲线y2＝ (x<0)交于点D．
(1)求直线CD对应的函数表达式及k的值．
(2)把菱形ABCD沿y轴的正方向平移多少个单位后，点C落在双曲线y2＝ (x<0)上？
(3)直接写出使y1>y2的自变量x的取值范围．
16、（8分）如图，已知在△ABC中，∠B=90°，AB=8cm，BC=6cm，点P开始从点A开始沿△ABC的边做逆时针运动，且速度为每秒1cm，点Q从点B开始沿△ABC的边做逆时针运动，且速度为每秒2cm，他们同时出发，设运动时间为t秒．
（1）出发2秒后，求PQ的长；
（2）在运动过程中，△PQB能形成等腰三角形吗？若能，则求出几秒后第一次形成等腰三角形；若不能，则说明理由；
17、（10分）如图，平行四边形ABCD中，对角线AC，BD相交于点O，点E，F分别是OB，OD的中点，试说明四边形AECF是平行四边形．
18、（10分）如图，直线过A（﹣1，5），P（2，a），B（3，﹣3）．
（1）求直线AB的解析式和a的值；
（2）求△AOP的面积．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）已知在△ABC中，∠ABC和∠ACB的角平分线交于O，且∠ABC的角平分线与∠ACB的外角平分线交于P，∠OPC和∠OCP角平分线交于H，∠H=117.5°，则∠A=________
20、（4分）已知点P（3﹣m，m）在第二象限，则m的取值范围是____________________．
21、（4分）如果P（2，m）,A (1, 1), B (4, 0)三点在同一直线上，则m的值为_________.
22、（4分）一次函数y＝(2m－6)x＋5中，y随x的增大而减小，则m的取值范围是 ________．
23、（4分）如图，直线与双曲线交于A、B两点，过点A作轴，垂足为M，连结BM，若，则k的值是______．
二、解答题（本大题共3个小题，共30分）
24、（8分）某超市预测某饮料会畅销、先用1800元购进一批这种饮料，面市后果然供不应求，又用8100元购进这种饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元．
（1）第一批饮料进货单价多少元？
（2）若两次进饮料都按同一价格销售，两批全部售完后，获利不少于2700元，那么销售单价至少为多少元？
25、（10分）如图①，在平面直角坐标系中，直线y=−12x+2与交坐标轴于A,B两点．以AB为斜边在第一象限作等腰直角三角形ABC，C为直角顶点，连接OC．
（1）求线段AB的长度
（2）求直线BC的解析式；
（3）如图②，将线段AB绕B点沿顺时针方向旋转至BD，且，直线DO交直线y=x+3于P点，求P点坐标．
26、（12分）某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务，这两家厂生产的皮具款式和材料都符合要求，因此只需要检测皮具质量的克数是否稳定，现从两家提供的样品中各抽取了6件进行检查，超过标准质量部分记为正数，不足部分记为负数，若该皮具的标准质量为500克，测得它们质量如下(单位：g)
(1)分别计算甲、乙两厂抽样检测的皮具总质量各是多少克？
(2)通过计算，你认为哪一家生产皮具的质量比较稳定？
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
分析：本题利用绝对值的化简和二次根式 的化简得出即可.
解析：∵x＜2，∴+|3﹣x|= .
故选D.
2、C
【解析】
根据常量的定义解答即可，常量是指在某一个变化过程中，固定不变的量．
【详解】
在以x为自变量， y为函数的关系式y=5πx中，常量为5π，
故选：C．
考查了变量关系中的常量的定义，熟记常量定义是解题的关键，注意π是常量．
3、B
【解析】
中位数，因图中是按从小到大的顺序排列的，所以只要找出最中间的一个数（或最中间的两个数）即可，本题是最中间的两个数；对于众数可由条形统计图中出现频数最大或条形最高的数据写出．
【详解】
由条形统计图中出现频数最大条形最高的数据是在第四组,故众数是2.4(万步)；
因图中是按从小到大的顺序排列的,最中间的步数都是2.3(万步),故中位数是2.3(万步).
故选B.
此题考查中位数，条形统计图，解题关键在于看懂图中数据
4、D
【解析】
过点D作DH⊥OB于点H，如图，根据角平分线的性质可得DH=DP=4，再根据三角形的面积即可求出结果．
【详解】
解：过点D作DH⊥OB于点H，如图，
∵OC是∠AOB的角平分线，DP⊥OA，DH⊥OB，
∴DH=DP=4，
∴△ODQ的面积=．
故选：D．
本题主要考查了角平分线的性质，属于基本题型，熟练掌握角平分线的性质定理是解题关键．
5、A
【解析】分析:根据上下平移时，b的值上加下减的规律解答即可.
详解:由题意得，
∵将直线y＝kx－1向上平移2个单位长度，
∴所得直线的解析式为：y＝kx－1+2= kx+1.
故选A.
点睛: 本题考查了一次函数图象的平移，一次函数图象的平移规律是：
①y=kx+b向左平移m个单位,是y=k(x+m)+b, 向右平移m个单位是y=k(x-m)+b,即左右平移时,自变量x左加右减；
②y=kx+b向上平移n个单位,是y=kx+b+n, 向下平移n个单位是y=kx+b-n，即上下平移时，b的值上加下减.
6、B
【解析】
根据题意可得小华步行上学时小华离学校的距离减小，而后离开家后不远便发现数学书忘在了家里，于是以相同的速度回家去拿时小华离学校的距离增大，到家后发现弟弟把牛奶洒在了地上，就放下手中的东西，收拾好后才离开距离不变，小华跑步到了学校时小华离学校的距离减小直至为1．
【详解】
解：根据题意可得小华步行上学时小华离学校的距离减小，而后离开家后不远便发现数学书忘在了家里，于是以相同的速度回家去拿时小华离学校的距离增大，到家后发现弟弟把牛奶洒在了地上，就放下手中的东西，收拾好后才离开距离不变，小华跑步到了学校时小华离学校的距离减小直至为1．
故选：B．
本题考查函数的图象，关键是根据题意得出距离先减小再增大，然后不变后减小为1进行判断．
7、B
【解析】
一次函数的图象是直线．
【详解】
解：表示y是x的一次函数的图象是一条直线，观察选项，只有B选项符合题意．
故选：B．
本题考查了函数的定义，一次函数和正比例函数的图象都是直线．
8、C
【解析】
根据加权平均数的公式进行计算即可得.
【详解】
=1.13（吨），
所以这100户平均节约用水的吨数为1.13吨，
故选C.
本题考查了加权平均数的计算，熟练掌握加权平均数的计算公式是解题的关键.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、y=100t-500（15＜t≤23）
【解析】
分析：
由题意可知，李明骑车的速度为100米/分钟，由此可知他从家到学校共用去了23分钟，其中自行车出故障前行驶了10分钟，自行车修好后行驶了8分钟，由此可知当时，y与t的函数关系为：.
详解：
∵车修好后，李明用8分钟骑行了800米，且骑车过程是匀速行驶的，
∴李明整个上学过程中的骑车速度为：100米/分钟，
∴在自行车出故障前共用时：1000÷100=10（分钟），
∵修车用了5分钟，
∴当时，是指小明车修好后出发前往学校所用的时间，
∴由题意可得：（），
化简得：（）.
故答案为：（）.
点睛：“由题意得到李明骑车的速度为100米/分钟，求时，y与t间的函数关系是求自行车修好后到家的距离与行驶的时间间的函数关系”是解答本题的关键.
10、1
【解析】
过点C作CE⊥AB，交AB的延长线于E，
∵∠ABC=150°，
∴∠CBE=30°，
在Rt△BCE中，∵BC=12，∠CBE=30°，
∴CE=BC=1．
故答案是1．
点睛：本题考查了含30°角的直角三角形的性质，解题的关键是作辅助线构造直角三角形．
11、m≤
【解析】
由关于x的一元二次方程x2﹣2x+4m=0有实数根，可知b2﹣4ac≥0，据此列不等式求解即可．
【详解】
解:由题意得，
4-4×1×4m≥0
解之得m≤
故答案为m≤．
本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式∆=b2﹣4ac：当∆>0时，一元二次方程有两个不相等的实数根；当∆=0时，一元二次方程有两个相等的实数根；当∆<0时，一元二次方程没有实数根．
12、.
【解析】
由勾股定理可得，由折叠的性质和平行线的性质可得，即可求的长.
【详解】
如图，
，，
，，
是的中点，
，
把沿折叠得到，
，，，
，
，
，
，
.
故答案为.
本题考查了翻折变换，直角三角形的性质，熟练运用折叠的性质是本题的关键.
13、1
【解析】
依据最喜欢羽毛球的学生数以及占被调查总人数的百分比，即可得到被调查总人数，进而得出最喜欢篮球的学生数以及最喜欢足球的学生数占被调查总人数的百分比．
【详解】
解：∵被调查学生的总数为10÷20%=50人，
∴最喜欢篮球的有50×32%=16人，
则最喜欢足球的学生数占被调查总人数的百分比= ×100%=1%．
故答案为：1．
本题考查扇形统计图，扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数．通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系．
三、解答题（本大题共5个小题，共48分）
14、（1）y＝1x﹣1；（1）2.
【解析】
（1）利用待定系数法把点A（0，-1），B（3，4）代入y=kx+b，可得关于k、b的方程组，再解出方程组可得k、b的值，进而得到函数解析式；
（1）把C（5，m）代入y=1x-1，即可求得m的值
【详解】
解：∵一次函数y＝kx+b的图象经过点A（0，﹣1），B（3，4），
∴，
解得：
∴这个一次函数的表达式为y＝1x﹣1．
（1）把C（5，m）代入y＝1x﹣1，得m＝1×5﹣1＝2．
此题主要考查了待定系数法求一次函数解析式和一次函数图象上点点坐标特征，熟练掌握待定系数法求一次函数步骤是解题的关键．
15、（1）；k＝－1.（2）把菱形ABCD沿y轴的正方向平移10个单位后，点C落在双曲线上；（3）x<－5.
【解析】
试题分析：（1）根据勾股定理求得AB的长，进而求得D、C的坐标，然后根据待定系数法即可求得直线CD的函数表达式及k的值；
（2）把x=-2代入y2=-（x＜0）得，y=-=10，即可求得平移的距离；
（3）根据函数的图象即可求得使y1＞y2的自变量x的取值范围．
试题解析：（1）∵点A的坐标为（0，4），点B的坐标为（3，0），
∴AB==5，
∵四边形ABCD是菱形，
∴AD=BC=AB=5，
∴D（-5，4），C（-2，0）．
∴，解得
∴直线CD的函数表达式为y1=-x-，
∵D点在反比例函数的图象上，
∴4=，
∴k=-1．
（2）∵C（-2，0），
把x=-2代入y2=-（x＜0）得，y=-=10，
∴把菱形ABCD沿y轴的正方向平移10个单位后，点C落在双曲线y2=（x＜0）上．
（3）由图象可知：当x＜-5时，y1＞y2．
16、（1）.
（2）能.当时.
【解析】
（1）利用勾股定理，根据题意求出PB和BQ的长，再由PB和BQ可以求得PQ的长；
（2）由题意可知P、Q两点是逆时针运动，则第一次形成等腰三角形是PB=QB，再列式即可得出答案.
【详解】
（1）由题意可得，，
因为t=2，所以，，
则由勾股定理可得.
（2）能.由题意可得，，又因为题意可知P、Q两点是逆时针运动，则第一次第一次形成等腰三角形是PB=QB，所以,即当时，第一次形成等腰三角形.
本题考查勾股定理、等腰三角形的性质和动点问题，属于综合题，难度适中，解题的关键是熟练掌握勾股定理、等腰三角形的性质.
17、见解析
【解析】
平行四边形的判定方法有多种，选择哪一种解答应先分析题目中给的哪一方面的条件多些，本题所给的条件为：平行四边形ABCD中，对角线AC，BD相交于点O，点E，F分别是OB，OD的中点，根据条件在图形中的位置，可选择利用“对角线相互平分的四边形为平行四边形”来解决．
【详解】
解：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD．
∵点E、F分别是OB、OD的中点，
∴OE=OF．
∴四边形AECF是平行四边形．（方法不唯一）
18、（2）-2（2）
【解析】
(2)设直线的表达式为y=kx+b，把点A. B的坐标代入求出k、b，即可得出答案； 把P点的坐标代入求出即可得到a；
(2)根据坐标和三角形面积公式求出即可．
【详解】
（2）设直线AB的解析式为y＝kx+b（k≠0），
将A（﹣2，5），B（2，﹣2）代入y＝kx+b，得：，
解得：，
∴直线AB的解析式为y＝﹣2x+2．
当x＝2时，y＝﹣2x+2＝﹣2，
∴点P的坐标为（2，﹣2），
即a的值为﹣2．
（2）设直线AB与y轴交于点D，连接OA，OP，如图所示．
当x＝0时，y＝﹣2x+2＝2，
∴点D的坐标为（0，2）．
S△AOP＝S△AOD+S△POD＝OD•|xA|+OD•|xP|＝×2×2+×2×2＝．
本题考查一元一次方程和直角坐标系的问题，解题的关键是掌握求解一元一次方程.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、70°
【解析】
根据三角形内角和定理，可得∠HCP+∠HPC=62.5°，由角平分线的性质，得∠OCP+∠OPC=125°，由三角形外角性质，得到∠BOC的度数，然后∠OBC+OCB=55°，然后可以计算得到∠A的度数.
【详解】
解：∵∠H=117.5°，
∴∠HCP+∠HPC=180°-117.5°=62.5°，
∵CH平分∠OCP，PH平分∠OPC，
∴∠OCP+∠OPC=2（∠HCP+∠HPC）= 125°，
∴∠BOC=125°，
∴∠OBC+∠OCB=180°-125°=55°，
∵BO平分∠ABC，CO平分∠ACB，
∴∠ABC+∠ACB=2（∠OBC+OCB）=110°，
∴∠A=180°-110°=70°；
故答案为：70°.
本题考查了角平分线的性质，三角形的内角和定理，三角形的外角性质，解题的关键是灵活运用性质求出有关的角度.
20、m>3.
【解析】
试题分析：因为点P在第二象限，所以，，解得：
考点：（1）平面直角坐标；（2）解不等式组
21、
【解析】
设直线的解析式为y=kx+b(k≠0)，
∵A(1,1)，B(4,0)，
，解之得 ，
∴直线AB的解析式为 ，
∵P(2,m)在直线上，
.
22、m＜1
【解析】
解：∵y随x增大而减小，
∴k＜0，
∴2m-6＜0，
∴m＜1．
23、1
【解析】
由题意得：S△ABM＝1S△AOM，又S△AOM＝|k|，则k的值可求出．
【详解】
解：设A（x，y），
∵直线与双曲线交于A、B两点，
∴B（−x，−y），
∴S△BOM＝|xy|，S△AOM＝|xy|，
∴S△BOM＝S△AOM，
∴S△ABM＝S△AOM＋S△BOM＝1S△AOM＝1，S△AOM＝|k|＝1，则k＝±1．
又由于反比例函数图象位于一三象限，
∴k＞0，故k＝1．
故答案为：1.
本题主要考查了反比例函数中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点．
二、解答题（本大题共3个小题，共30分）
24、 (1)4元/瓶．(2) 销售单价至少为1元/瓶．
【解析】
（1）设第一批饮料进货单价为x元/瓶，则第二批饮料进货单价为（x+2）元/瓶，根据数量＝总价÷单价结合第二批购进饮料的数量是第一批的3倍，即可得出关于x的分式方程，解之经检验后即可得出结论；
（2）由数量＝总价÷单价可得出第一、二批购进饮料的数量，设销售单价为y元/瓶，根据利润＝销售单价×销售数量﹣进货总价结合获利不少于2100元，即可得出关于y的一元一次不等式，解之取其最小值即可得出结论．
【详解】
（1）设第一批饮料进货单价为x元/瓶，则第二批饮料进货单价为（x+2）元/瓶，
依题意，得：＝3×，
解得：x＝4，
经检验，x＝4是原方程的解，且符合题意．
答：第一批饮料进货单价是4元/瓶；
（2）由（1）可知：第一批购进该种饮料450瓶，第二批购进该种饮料1350瓶．
设销售单价为y元/瓶，
依题意，得：（450+1350）y﹣1800﹣8100≥2100，
解得：y≥1．
答：销售单价至少为1元/瓶．
本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据各数量之间的关系，正确列出一元一次不等式．
25、（1）；（2）；（3）P点的坐标是.
【解析】
（1）先确定出点A，B坐标，利用勾股定理计算即可；
（2）如图1中，作CE⊥x轴于E，作CF⊥y轴于F，进而判断出，即可判断出四边形OECF是正方形，求出点C坐标即可解决问题．
（3）如图2中，先判断出点B是AM的中点，进而求出M的坐标，即可求出DP的解析式，联立成方程组求解即可得出结论．
【详解】
解：（1）∵直线交坐标轴于A、B两点．
∴令，，∴B点的坐标是，
，
令，，∴A点的坐标是，
，
根据勾股定理得：.
（2）如图，作CE⊥x轴于E，作CF⊥y轴于F，
∴四边形OECF是矩形．
∵是等腰直角三角形，
，，，
，
，，．
∴四边形OECF是正方形，
，
，，．
∴C点坐标
设直线BC的解析式为：，
∴将、代入得：，
解得：，．
∴直线BC的解析式为：.
（3）延长AB交DP于M，
由旋转知，BD＝AB，
∴∠BAD＝∠BDA，
∵AD⊥DP，
∴∠ADP＝90°，
∴∠BDA＋∠BDM＝90°，∠BAD＋∠AMD＝90°，
∴∠AMD＝∠BDM，
∴BD＝BM，
∴BM＝AB，
∴点B是AM的中点，
∵A（4，0），B（0，2），
∴M（−4，4），
∴直线DP的解析式为y＝−x，
∵直线DO交直线y＝x＋3于P点，
将直线与联立得：
解得：
∴P点的坐标是.
此题是一次函数综合题，主要考查了待定系数法求函数解析式，一次函数的图像和性质，全等三角形的判定和性质，等腰三角形的判定和性质等，解（2）的关键是求出点C的坐标，解（3）的关键是证明点B是AM的中点，求出直线DP的解析式．
26、 (1)甲厂抽样检测的皮具总质量为3000克，乙厂抽样检测的皮具总质量为3000克；(2)乙公司生产皮具的质量比较稳定．
【解析】
(1)求出记录的质量总和，再加上标准质量即可；
(2)以标准质量为基准，根据方差的定义求出两公司的方差，相比即可.
【详解】
解：(1)甲厂抽样检测的皮具总质量为500×6+(﹣3+0+0+1+2+0)＝3000(克)，
乙厂抽样检测的皮具总质量为500×6+(﹣2+1﹣1+0+1+1)＝3000(克)；
(2)∵＝×(﹣3+0+0+1+2+0)＝0，
∴＝×[(﹣3﹣0)2+(0﹣0)2×3+(1﹣0)2+(2﹣0)2]≈2.33，
∵＝×(﹣2+1﹣1+0+1+1)＝0，
∴＝×[(﹣2﹣0)2+3×(1﹣0)2+(﹣1﹣0)2+(0﹣0)2]≈1.33，
∵＜，
∴乙公司生产皮具的质量比较稳定．
本题主要考查了方差，用“先平均，再求差，然后平方，最后再平均”得到的结果表示一组数据偏离平均值的情况，这个结果叫方差．
题号
一
二
三
四
五
总分
得分
批阅人
每户节水量（单位：吨）
1
1.2
1.5
节水户数
65
15
20
类别
A
B
C
D
E
F
类型
足球
羽毛球
乒乓球
篮球
排球
其他
人数
10
4
6
2
厂家
超过标准质量的部分
甲
﹣3
0
0
1
2
0
乙
﹣2
1
﹣1
0
1
1