广东省佛山市顺德区2023-2024学年八年级（下）期末数学试卷

展开

这是一份广东省佛山市顺德区2023-2024学年八年级（下）期末数学试卷，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题：本题共8小题，每小题3分，共24分。在每小题给出的选项中，只有一项是符合题目要求的。
1．若分式x+2x的值为零，则x等于（）
A．−2B．0C．2D．0和−2
2．若a>b，则下列变形正确的是( )
A．a−6b+2D．a23．正六边形的内角和是( )
A．720°B．540°C．360°D．180°
4．下列由左边到右边的变形是因式分解的是（）
A．x2−2x−3=x(x−2)−3B．x2+y2=(x+y)2
C．(x+1)(x−3)=x2−2x−3D．x2−x=x(x−1)
5．用反证法证明“一个三角形中不能有两个角是直角”时，第一步假设( )
A．三角形中有一个内角是直角B．三角形中有两个内角是直角
C．三角形中有三个内角是直角D．三角形中不能有内角是直角
6．若x+1x=3，则x2+1x2=( )
A．11B．9C．7D．5
7．四边形ABCD的对角线AC、BD相交于点O，不能判定四边形ABCD是平行四边形的条件是( )
A．AB//CD，AB=CDB．AB//CD，AD//BC
C．OA=OC，OB=ODD．AB//CD，AD=BC
8．用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的镶嵌.给出以下多边形：①等边三角形，②正方形，③正五边形，④正六边形，能单独进行平面图形的镶嵌的有( )
A．①②③B．①②④C．①③④D．②③④
二、填空题：本题共5小题，每小题3分，共15分。
9．因式分解：x2+2x= ．
10．在平行四边形ABCD中，∠A=50°，则∠C= °.
11．不等式的解集如图所示，写出一个符合要求的不等式：．
12．若x2+kx+1是一个完全平方式，则k的值是．
13．在△ABC中，AB=6，∠A=30°，若符合该条件的△ABC有两个，则BC长的范围为．
三、解答题：本题共9小题，共81分。解答应写出文字说明，证明过程或演算步骤。
14．（1）解关于x的方程1x+5+10x2−25=0；
（2）求代数式(3+yx)÷9x2−y2x的值，其中x=−16，y=2．
15．已知不等式组2x+5<3x+6x−1（1）求不等式组①的解集；
（2）若不等式组2x<1+ax>3+2b的解集与①的解集相同，求a、b的值．
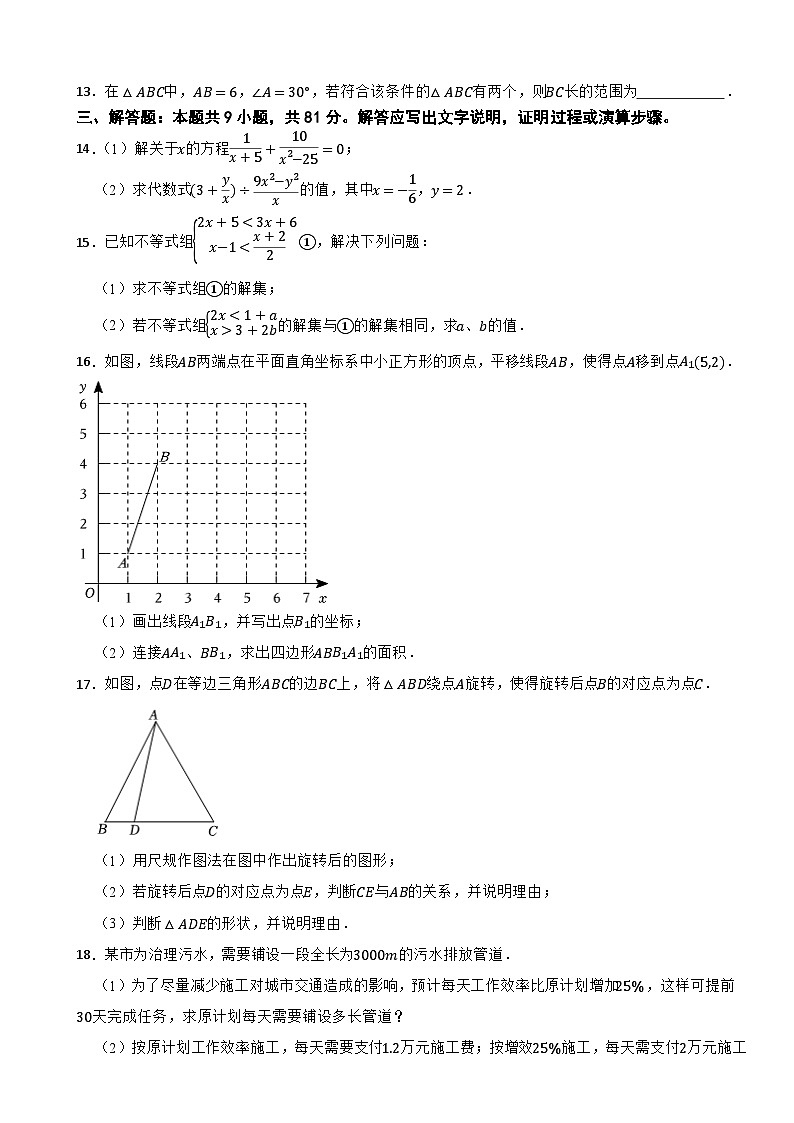
16．如图，线段AB两端点在平面直角坐标系中小正方形的顶点，平移线段AB，使得点A移到点A1(5,2)．
（1）画出线段A1B1，并写出点B1的坐标；
（2）连接AA1、BB1，求出四边形ABB1A1的面积．
17．如图，点D在等边三角形ABC的边BC上，将△ABD绕点A旋转，使得旋转后点B的对应点为点C．
（1）用尺规作图法在图中作出旋转后的图形；
（2）若旋转后点D的对应点为点E，判断CE与AB的关系，并说明理由；
（3）判断△ADE的形状，并说明理由．
18．某市为治理污水，需要铺设一段全长为3000m的污水排放管道．
（1）为了尽量减少施工对城市交通造成的影响，预计每天工作效率比原计划增加25%，这样可提前30天完成任务，求原计划每天需要铺设多长管道？
（2）按原计划工作效率施工，每天需要支付1.2万元施工费；按增效25%施工，每天需支付2万元施工费.在(1)条件下，若完成工程所需施工费用不超过236万元，求按原计划工作效率施工至少多少天？
19．如图，点O为平行四边形ABCD的对称中心，经过点O的直线交边AD于点M，交BA的延长线于点E，交边BC于点N，交DC的延长线于点F．
（1）若∠BON=90°，∠DBC=30°，ON=1，求BD的长；
（2）连接BM、DN，判断四边形DMBN的形状，并证明；
（3）求证：EM=FN．
20．已知函数y1=2x−1，y2=3−x，解决下列问题：
（1）若y1>y2，求x的取值范围；
（2）若4x+3(2x−1)(3−x)=Ay1+By2，求实数A、B；
（3）若分式y1−1y2的值是正整数，求满足条件的所有整数x的值．
21．学习几何时，通常是先用几何的眼光去观察，再用代数的方法去验证.网格是研究几何图形的一种工具，也是培养几何直观的一种方式．
（1）如图是正方形网格，正方形的顶点称为格点，每一个小正方形的边长为1．
①如图1，点A、B在格点上，仅用无刻度的直尺找出线段AB的中点O(不写画法，保留画图痕迹)；
②如图2，点A、B、C在格点上，仅用无刻度的直尺找出∠A的平分线交BC于点P，并写出画图的步骤或依据；
（2）如图3，在△ABC中，AB=1，AC=2，BC=5，以AC为边在AC的左侧作等腰直角△ACD，连接BD，求BD的长．
22．在△ABC中，∠C=90°，点M是线段BC上的一点，连接AM．
（1）如图1，AC=BC，AM是△ABC的角平分线，ME⊥AB于点E．
①当CM=4时，求AB的长；
②若△ABC的中线CO交AM于点F，判断CF与ME的关系，并说明理由；
（2）如图2，若BM=AC，点N是AC上的一点，且AN=CM，连接BN交AM于点P，求∠BPM的度数．
答案解析部分
1．【答案】A
【知识点】分式的值为零的条件
【解析】【解答】解：∵ 分式x+2x的值为零，
∴x+2=0且x≠0，
解之：x=-2.
故答案为：A.
【分析】利用分式值为0的条件：分子等于0且分母不等于0，可得到关于x的方程和不等式，然后分别求解，可得到x的值.
2．【答案】C
【知识点】不等式的性质
【解析】【解答】解：∵a>b，
A、a−6>b−6，A不符合题意；
B、3a>3b，B不符合题意；
C、a+2>b+2，C符合题意；
D、a2故答案为：C
【分析】根据不等式的性质结合题意对选项逐一分析即可求解。
3．【答案】A
【知识点】多边形的内角和公式
【解析】【解答】解：由题意得正六边形的内角和是（6-2）×180°=720°，
故答案为：A
【分析】根据多边形的内角和公式（n-2）×180°结合题意即可求解。
4．【答案】D
【知识点】因式分解的概念
【解析】【解答】解：A．等式的右边不是几个整式的积的形式，不是因式分解，故此选项不符合题意；
B．等式左右两边不相等，不是因式分解，故此选项不符合题意；
C．原变形是整式乘法，不是因式分解，故此选项不符合题意；
D．把一个多项式化为几个整式的积的形式，原变形是因式分解，故此选项符合题意；
故答案为：D
【分析】根据因式分解的定义：将和差的形式变为乘积的形式可得答案。
5．【答案】B
【知识点】反证法
【解析】【解答】解：用反证法证明：“三角形中不能两个直角”时，
第一步先假设三角形中有两个内角是直角，
故答案为：B
【分析】根据反证法的定义结合反证法的步骤：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立，进而即可求解。
6．【答案】C
【知识点】完全平方公式及运用
【解析】【解答】解：∵x+1x=3，
∴(x+1x)2=9，
∴x2+1x2+2=9，
∴x2+1x2=7，
故答案为：B
【分析】根据完全平方公式结合题意得到x2+1x2+2=9，进而即可求解。
7．【答案】D
【知识点】平行四边形的判定
【解析】【解答】解：A、∵AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形，A不符合题意；
B、∵AB∥CD，AB=CD，
∴四边形ABCD是平行四边形，B不符合题意；
C、∵OA=OC，OB=OD，
∴四边形ABCD是平行四边形，C不符合题意；
D、由AB∥CD，AD=BC不能判定四边形ABCD是平行四边形，D符合题意，
故答案为：D
【分析】根据平行四边形的判定结合题意对选项逐一判断即可求解。
8．【答案】B
【知识点】平面镶嵌（密铺）
【解析】【解答】解：①等边三角形的内角和是180°，180°×2=360°，能镶嵌；
②正方形的内角和是360°，能镶嵌；
③正五边形的每个内角是108°，不能镶嵌；
④正六边形的每个内角是120°，120°×3=360°，能镶嵌；
故答案为：B
【分析】根据平面面镶嵌（密铺）的定义：判断一种或几种图形是否能够镶嵌，要看一看拼在同一顶点处的几个角能否构成周角，若能构成360°，则说明能够进行平面镶嵌，反之则不能判断即可求解。
9．【答案】x（x+2）
【知识点】因式分解﹣提公因式法
【解析】【解答】解：原式=x（x+2），
故答案为：x（x+2）．
【分析】直接利用提公因式法分解即可。
10．【答案】50
【知识点】平行四边形的性质
【解析】【解答】解：∵四边形ABCD为平行四边形，
∴∠C=∠A=50°，
故答案为：50°
【分析】根据平行四边形的性质（对角相等）结合题意即可求解。
11．【答案】x−4>0（答案不唯一）
【知识点】在数轴上表示不等式的解集
【解析】【解答】解：由数轴可知此不等式的解集为x＞4，
∴这个不等式可以是x-4＞0.
故答案为：x-4＞0（答案不唯一）
【分析】利用数轴可得到不等式的解集，再写出一个符合题意的不等式.
12．【答案】±2
【知识点】完全平方式
【解析】【解答】解：∵x2+kx+1是一个完全平方式，
∴k=±2，
故答案为：±2
【分析】根据完全平方式的定义结合题意即可得到k的值.
13．【答案】3【知识点】垂线段最短及其应用；含30°角的直角三角形
【解析】【解答】解：过点B作BE⊥AD于点E，如图所示：
∵∠A=30°，∠BEA=90°，
∴BE=12AB=3，
∵垂线段最短
∴当点C在点E处时，符合条件的△ABC只有一个，
∴当点C在AE上时，在点E的右侧射线ED还有一个点能使此点与点B间的距离与BC的长度相等，
故符合条件的△ABC只有两个，
∴3故答案为：3【分析】过点B作BE⊥AD于点E，根据含30°角的直角三角形的性质得到BE=12AB=3，进而根据垂线段最短得到当点C在点E处时，符合条件的△ABC只有一个，从而得到当点C在AE上时，在点E的右侧射线ED还有一个点能使此点与点B间的距离与BC的长度相等，
故符合条件的△ABC只有两个，再结合题意即可得到BC的取值.
14．【答案】（1）解：去分母，得x−5+10=0，
解得x=−5，
检验：当x=−5时，(x+5)(x−5)=0，所以x=−5为原方程的增根，
所以原方程无解；
（2）解：原式=3x+yx⋅x(3x+y)(3x−y)
=13x−y，
当x=−16，y=2时，原式=13×(−16)−2=−25．
【知识点】解分式方程；分式的化简求值-直接代入
【解析】【分析】（1）根据题意去分母即可解分式方程，进而检验即可求解；
（2）根据分式的混合运算化简，进而代入即可求解。
15．【答案】（1）解：由2x+5<3x+6得：x>−1，
由x−1则不等式组的解集为−1（2）解：由2x<1+a得：x<1+a2，
由x>3+2b且该不等式组的解集与①的解集相同知，1+a2=4且3+2b=−1，
解得a=7，b=−2．
【知识点】解一元一次不等式组；一元一次不等式组的特殊解；一元一次不等式组的含参问题
【解析】【分析】（1）先根据题意解不等式，进而即可得到不等式组的解集；
（2）根据题意解不等式得到x<1+a2，进而根据题意即可得到1+a2=4且3+2b=−1，从而即可得到a和b.
16．【答案】（1）解：由题意得，线段AB向右平移4个单位长度，向上平移1个单位长度得到线段A1B1，
如图，线段A1B1即为所求．
由图可得，点B1的坐标为(6,5)．
（2）解：四边形ABB1A1的面积为5×4−12×4×1−12×(1+4)×1−12×4×1−12×(1+4)×1=20−2−52−2−52=11．
【知识点】作图﹣平移；几何图形的面积计算-割补法
【解析】【分析】（1）根据作图-平移根据线段AB向右平移4个单位长度，向上平移1个单位长度得到线段A1B1，进而即可求解；
（2）根据割补法结合题意计算面积即可求解。
17．【答案】（1）解：如图，△ACE为所作；
（2）解：AB//CE．
理由如下：
∵△ABC为等边三角形，
∴∠B=∠ACB=60°，
∵△ABD绕点A旋转得到△ACE，
∴∠ACE=∠B=60°，
∴∠BCE=120°，
∴∠B+∠BCE=180°，
∴AB//CE；
（3）解：△ADE是等边三角形，
理由：连接DE，
∵△ABC是等边三角形，
∴AB=AC，∠BAC=60°，
∵△ABD绕点A旋转得到△ACE，
∴AD=AE，∠DAE=∠BAC=60°，
∴△ADE是等边三角形．
【知识点】等边三角形的判定与性质；旋转的性质；作图﹣旋转
【解析】【分析】（1）根据作图-旋转即可求解；
（2）先根据等边三角形的性质得到∠B=∠ACB=60°，进而根据旋转的性质得到∠ACE=∠B=60°，从而结合题意得到∠B+∠BCE=180°，再根据平行线的判定即可求解；
（3）连接DE，根据等边三角形的性质得到AB=AC，∠BAC=60°，进而根据旋转的性质得到AD=AE，∠DAE=∠BAC=60°，再根据等边三角形的判定即可求解。
18．【答案】（1）解：设原计划每天需要铺设x m长管道，则增效后每天需要铺设(1+25%)x m长管道，
由题意得：3000x−3000(1+25%)x=30，
解得：x=20，
经检验，x=20是原方程的解，且符合题意，
答：原计划每天需要铺设20m长管道；
（2）解：由(1)可知，(1+25%)×20=25(m)，
设按原计划工作效率施工a天，则增效25%施工(3000−20a25)天，
由题意得：1.2a+2×(3000−20a25)≤236，
解得：a≥10，
答：按原计划工作效率施工至少10天．
【知识点】一元一次不等式的应用；分式方程的实际应用-工程问题
【解析】【分析】（1）设原计划每天需要铺设x m长管道，则增效后每天需要铺设(1+25%)x m长管道，根据题意即可列出分式方程，从而即可求解；
（2）先根据(1)可知，(1+25%)×20=25(m)，设按原计划工作效率施工a天，则增效25%施工(3000−20a25)天，根据“按原计划工作效率施工，每天需要支付1.2万元施工费；按增效25%施工，每天需支付2万元施工费.在(1)条件下，若完成工程所需施工费用不超过236万元”即可列出不等式，从而即可求出a的取值。
19．【答案】（1）解：解：∵∠BON=90°，∠DBC=30°，ON=1，
∴BN=2ON=2，
∴OB=22−12=3，
∵点O为平行四边形ABCD的对称中心，
∴OB=OD=3，
∴BD=23；
（2）解：四边形DMBN是平行四边形，理由如下：
如图1，四边形ABCD是平行四边形，
∴AD//BC，
∴∠ADB=∠CBD，
∵OB=OD，∠DOM=∠BON，
∴△BON≌△DOM(ASA)，
∴BN=DM，
∴四边形DMBN是平行四边形；
（3）证明：由(2)知：△BON≌△DOM，
∴OM=ON，
∵四边形ABCD是平行四边形，
∴AB//CD，
∴∠ABD=∠FDO，∠E=∠F，
∵OB=OD，
∴△EBO≌△FDO(AAS)，
∴OE=OF，
∴OE−OM=OF−ON，
即EM=FN．
【知识点】三角形全等的判定；含30°角的直角三角形；平行四边形的判定与性质；中心对称的性质
【解析】【分析】（1）先根据题意结合含30°角的直角三角形的性质得到BN=2，进而运用勾股定理求出OB，再根据对称中心的定义结合题意即可求解；
（2）根据平行四边形的性质结合平行线的性质得到∠ADB=∠CBD，进而根据三角形全等的判定与性质证明△BON≌△DOM(ASA)得到BN=DM，从而根据平行四边形的判定即可求解；
（3）根据三角形全等的性质得到OM=ON，进而根据平行四边形的性质结合平行线的性质得到∠ABD=∠FDO，∠E=∠F，再根据三角形全等的判定与性质证明△EBO≌△FDO(AAS)得到OE=OF，从而即可求解。
20．【答案】（1）解：由题意，∵y1>y2，
∴2x−1>3−x．
∴x>43．
（2）解：由题意得，Ay1+By2=A2x−1+B3−x=A(3−x)+B(2x−1)(2x−1)(3−x)=(−A+2B)x+3A−B(2x−1)(3−x)．
又4x+3(2x−1)(3−x)=(−A+2B)x+3A−B(2x−1)(3−x)，
∴−A+2B=43A−B=3．
∴A=2B=3．
（3）解：由题意得，y1−1y2=2x−23−x=−2(x−3)+4x−3=−2−4x−3．
又∵y1−1y2为正整数，
∴x−3为4的因数，即x−3=±1，±2，±4．
∴只有当x−3=−1时符合题意．
∴x=2．
【知识点】分式的混合运算；解二元一次方程组；解一元一次不等式
【解析】【分析】（1）根据题意列出不等式，从而即可求解；
（2）先根据分式的混合运算计算Ay1+By2=A2x−1+B3−x=A(3−x)+B(2x−1)(2x−1)(3−x)=(−A+2B)x+3A−B(2x−1)(3−x)，进而即可得到−A+2B=43A−B=3，从而解二元一次方程组即可求解；
（3）根据题意代入得到y1−1y2=2x−23−x=−2(x−3)+4x−3=−2−4x−3．从而根据正整数的定义结合题意即可求解。
21．【答案】（1）解：①如图，点O即为所求；
②如图，在AC的延长线上取点取格点E,J，取格点F，连接FJ,BE交与点G，连接AG交BC于点P，则AP即为所求；
理由：根据作法得：AB=32+42=5,AE=5，四边形BFEJ是矩形，
∴AB=AE，BG=EG，
∴AP平分∠BAC；
（2）解：∵AB=1，AC=2，AB=5，
∴AB2+AC2=BC2，
∴∠CAB=90°，
有三种情形：
①当∠CAD'=90°，CA=AD'=2时，BD'=1+2=3；
②当∠ACD=90°，AC=CD=2时，BD=22+32=13；
③当∠AD″C=90°，BD″=22+12=5．
综上所述，BD的长为3或13或5．
【知识点】勾股定理；勾股定理的逆定理；尺规作图-直线、射线、线段；尺规作图-作角的平分线
【解析】【分析】（1）①取格点M，N，连接MN交AB于点O，即可求解；
②在AC的延长线上取点取格点E,J，取格点F，连接FJ,BE交与点G，连接AG交BC于点P，则AP即为所求；
（2）先根据勾股定理的逆定理得到∠CAB的度数，进而即可得到三种情形：①当∠CAD'=90°，CA=AD'=2时，②当∠ACD=90°，AC=CD=2时，③当∠AD″C=90°，从而根据勾股定理即可求解。
22．【答案】（1）解：①设AC=BC=x，
∵AM是△ABC的角平分线，ME⊥AB，
则CM=ME=4，则BM=x−4，
在等腰直角三角形BEM中，BM=2ME，
即x−4=42，则x=4+42，
则AB=2x=8+42；
②CF=ME且CF//ME，理由：
如图，∵CO为直线，△ABC为等腰直角三角形，
则CO⊥AB，
而ME⊥AB，则ME//CO，即CF//ME，
则∠EMA=∠MFC，
由①知，EM=CM，AM=AM，
则RtAME△≌Rt△AMC(HL)，
则∠EMA=∠MFC=∠EMA，
则FC=CM=EM，
即CF=ME且CF//ME；
（2）解：如图，过M作ME//AN，使ME=AN，连NE，BE，
则四边形AMEN为平行四边形，
∴NE=AM，ME⊥BC，
∵AN=MC，
∴ME=CM，
在△BEM和△AMC中，
ME=MC∠EMB=∠MCA=90°BM=AC，
∴△BEM≌△AMC(SAS)，
∴BE=AM=NE，∠1=∠2，∠3=∠4，
∵∠1+∠3=90°，
∴∠2+∠4=90°且BE=NE，
∴△BEN为等腰直角三角形，∠BNE=45°，
∵AM//NE，
∴∠BPM=∠BNE=45°．
【知识点】平行线的性质；三角形全等的判定；角平分线的性质；平行四边形的性质
【解析】【分析】（1）①设AC=BC=x，根据角平分线的性质得到CM=ME=4，BM=x−4，再根据等腰直角三角形的性质得到BM=2ME，进而结合题意即可求出x，从而得到AB；
②根据等腰直角三角形的性质得到CO⊥AB，进而根据象限的性质得到∠EMA=∠MFC，由①知，EM=CM，AM=AM，从而根据三角形全等的判定与性质证明RtAME△≌Rt△AMC(HL)得到∠EMA=∠MFC=∠EMA，从而根据等腰三角形的判定结合题意即可求解；
（2）过M作ME//AN，使ME=AN，连NE，BE，则四边形AMEN为平行四边形，根据平行四边形的性质得到NE=AM，ME⊥BC，等量代换得到ME=CM，再根据三角形全等的判定与性质证明△BEM≌△AMC(SAS)得到BE=AM=NE，∠1=∠2，∠3=∠4，从而结合题意运用等腰直角三角形的判定与性质得到∠BNE=45°，再根据平行线的性质即可求解。

广东省佛山市顺德区2023-2024学年八年级（下）期末数学试卷

更专业

更丰富

更便捷

真低价

欢迎来到教习网