江苏省泰州市姜堰区励才实验学校2023-2024学年七年级上学期期中数学试题

这是一份江苏省泰州市姜堰区励才实验学校2023-2024学年七年级上学期期中数学试题，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）2023的相反数等于（ ）
A．2023B．﹣2023C．12023D．-12023
2．（3分）结果不等于﹣213的算式是（ ）
A．-2-13B．-(2+13)
C．(-2)+(-13)D．-2+13
3．（3分）神舟十三号载人飞船返回舱搭载的12000粒种子顺利出舱．用科学记数法表示12000是（ ）
A．1.2×104B．12×103C．0.12×105D．12×105
4．（3分）单项式-32x2y3的系数和次数分别为（ ）
A．﹣3，5B．-32，5C．﹣3，6D．-32，6
5．（3分）下列各对数中，互为相反数的是（ ）
A．﹣23与﹣32B．（﹣2）3与﹣23
C．（﹣3）2与﹣32D．-223与(23)2
6．（3分）多项式x+2y与x﹣2的大小关系（ ）
A．只与x有关B．只与y有关C．与x、y有关D．与x、y无关
二、填空题（本大题共10小题，每小题3分，共30分．请把答案填写在答题卡相应位置上）
7．（3分）﹣3的绝对值是 ．
8．（3分）若x＝﹣1是方程2x﹣m＝0的解，则m等于 ．
9．（3分）一天早晨的气温是﹣3℃，中午上升了11℃，半夜又下降了9℃，半夜的气温是 ℃．
10．（3分）若﹣xay2与5x4y2是同类项，则常数a的值为 ．
11．（3分）已知a，b为有理数，且|a+1|+（2023﹣b）2＝0，则ab＝ ．
12．（3分）某市出租车的收费标准是：起步价为8元，起步里程为3km（3km以内按起步价付费），3km后每千米收2元．某人乘出租车从甲地到乙地共付费16元．设甲、乙两地之间的路程为x km，可得方程 ．
13．（3分）代数式﹣2a+1与1+4a互为相反数，则a＝ ．
14．（3分）若x2+x加上一个多项式的和是2x2+x+1，则这个多项式是 ．
15．（3分）有理数a，b在数轴上的位置如图：
则下列结论：①ab＜0；②a+b＞0；③b﹣a＞0；④|a﹣b|＝a﹣b； ⑤﹣3＜﹣b＜﹣2．其中结论正确的是 （填序号）．
16．（3分）我国“华为”公司是世界通讯领域的龙头企业，某款手机后置摄像头模组如图所示．其中大圆的半径为r，中间小圆的半径为12r，4个半径为15r的高清圆形镜头分布在两圆之间．请用含r的代数式表示图中阴影部分的面积 ．
三、解答题（本大题共102分．请在答题纸指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（16分）计算：
（1）﹣3﹣8+5﹣7；
（2）34+(-12)-(-78)÷(-78)；
（3）-24×(-12+34-23)；
（4）-42÷(-3)3×(32)3-|13-3|．
18．（8分）化简：
（1）﹣3x+2y﹣6x﹣9y；
（2）（5a+3b）﹣（2a﹣5b）．
19．（6分）解方程：-12x+1＝3+x．
20．（10分）先化简再求值：4a2+3（b2﹣2ab）﹣2（2a2﹣ab），其中a=-12，b=-3．
21．（10分）请画数轴，并完成以下内容：
（1）在数轴上表示下列各数：0，﹣|+2|，-(-52)，72，π；
（2）把以上5个数用“＜”号连接起来．
22．（8分）电影《万里归途》成为了国庆假期市民观影的首选．某市9月30日该电影票的售票量为1.1万张，10月1日至10月7日售票量（单位，万张）的变化如下表（“+”表示售票量比前一天多，“﹣”表示售票量比前一天少）：
请根据以上信息，回答下列问题：
（1）10月2日的售票量为多少万张？
（2）10月7日与9月30日相比较，哪一天的售票量多？
（3）若平均每张票价为45元，则10月1日到10月7日某市《万里归途》的票房收入多少万元？
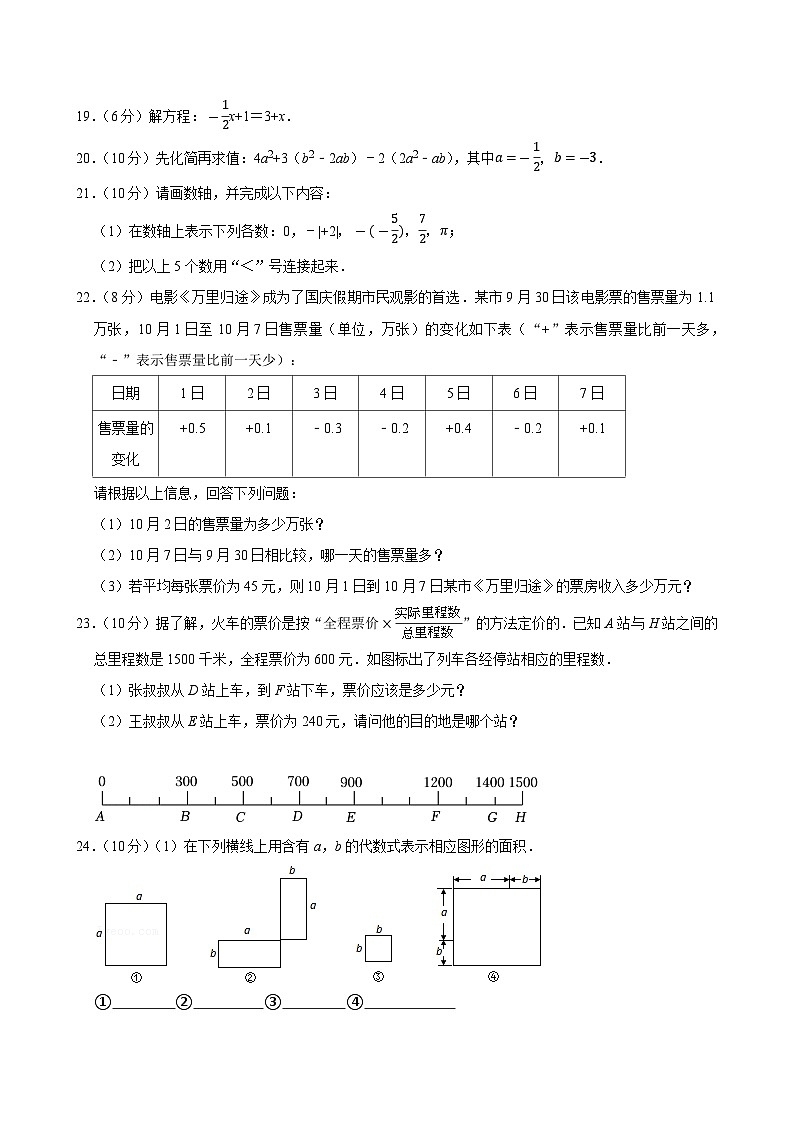
23．（10分）据了解，火车的票价是按“全程票价×实际里程数总里程数”的方法定价的．已知A站与H站之间的总里程数是1500千米，全程票价为600元．如图标出了列车各经停站相应的里程数．
（1）张叔叔从D站上车，到F站下车，票价应该是多少元？
（2）王叔叔从E站上车，票价为240元，请问他的目的地是哪个站？
24．（10分）（1）在下列横线上用含有a，b的代数式表示相应图形的面积．
① ② ③ ④
（2）请在图④画出拼图并通过拼图，你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表达： ．
（3）利用（2）的结论计算10.232+20.46×9.77+9.772的值．
25．（12分）已知：A=32x2-xy+1，B=5x2+4xy-2，
（1）求2A﹣B（用含x、y的代数式表示）；
（2）若x2+3xy=34，求2A﹣B值．
26．（12分）【实际问题】
某商场在双十一期间为了鼓励消费，设计了抽奖活动，方案如下：根据不同的消费金额，每次抽奖时可以从100张面值分别为1元、2元、3元、…、100元的奖券中（面值为整数），一次任意抽取2张、3张、4张、…等若干张奖券，奖券的面值金额之和即为优惠金额．某顾客获得了一次抽取5张奖券的机会，小明想知道该顾客共有多少种不同的优惠金额？
【问题建模】
从1，2，3，…，n（n为整数，且n＞5）这n个整数中任取5个整数，这5个整数之和共有多少种不同的结果？
【模型探究】
我们采取一般问题特殊化的策略，先从最简单的情形入手，从中找出解决问题的方法．从1，2，3这3个整数中任取2个整数，这2个整数之和共有多少种不同的结果？
如表所示：所取的2个整数之和可以为3，4，5，也就是从3到5的连续整数，其中最小是3，最大是5，所以共有3种不同的结果．
（1）从1，2，3，4，5这5个整数中任取2个整数，这2个整数之和共有 种不同的结果．
（2）从1，2，3，…，n（n为整数，且n＞5）这n个整数中任取3个整数，这3个整数之和共有 种不同的结果．
（3）归纳结论：从1，2，3，…，n（n为整数，且n＞5）这n个整数中任取5个整数，这5个整数之和共有 种不同的结果．
【问题解决】
从100张面值分别为1元、2元、3元、…、100元的奖券中（面值为整数），一次任意抽取5张奖券，共有 种不同的优惠金额．
【问题拓展】
从3，4，5，…，n（n为整数，且n＞5）这n个整数中任取5个整数，使得取出的这些整数之和共有121种不同的结果，求n的值．（写出解答过程）
2023-2024学年江苏省泰州市姜堰区励才实验学校七年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共6小题，每小题3分，共18分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题纸相应位置上）
1．（3分）2023的相反数等于（ ）
A．2023B．﹣2023C．12023D．-12023
【解答】解：2023的相反数等于﹣2023．
故选：B．
2．（3分）结果不等于﹣213的算式是（ ）
A．-2-13B．-(2+13)
C．(-2)+(-13)D．-2+13
【解答】解：∵﹣2-13=-213，﹣（2+13）＝﹣213，（﹣2）+（-13）＝﹣213，而﹣2+13=-53，
∴选项A，B，C不符合题意，选项D符合题意，
故选：D．
3．（3分）神舟十三号载人飞船返回舱搭载的12000粒种子顺利出舱．用科学记数法表示12000是（ ）
A．1.2×104B．12×103C．0.12×105D．12×105
【解答】解：12000＝1.2×104．
故选：A．
4．（3分）单项式-32x2y3的系数和次数分别为（ ）
A．﹣3，5B．-32，5C．﹣3，6D．-32，6
【解答】解：单项式-32x2y3的系数和次数分别为-32和5．
故选：B．
5．（3分）下列各对数中，互为相反数的是（ ）
A．﹣23与﹣32B．（﹣2）3与﹣23
C．（﹣3）2与﹣32D．-223与(23)2
【解答】解：A、1个﹣8，1个﹣9，不是互为相反数，故A错误；
B、都等于﹣8，故B错误；
C、只有符号不同的两个数互为相反数，故C正确；
D、1个-43，1个49，不是互为相反数，故D错误．
故选：C．
6．（3分）多项式x+2y与x﹣2的大小关系（ ）
A．只与x有关B．只与y有关C．与x、y有关D．与x、y无关
【解答】解：∵（x+2y）﹣（x﹣2）
＝x+2y﹣x+2
＝2y+2，
∴x+2y与x﹣2的差只与y有关．
故选：B．
二、填空题（本大题共10小题，每小题3分，共30分．请把答案填写在答题卡相应位置上）
7．（3分）﹣3的绝对值是 3 ．
【解答】解：|﹣3|＝3．
故答案为：3．
8．（3分）若x＝﹣1是方程2x﹣m＝0的解，则m等于 ﹣2 ．
【解答】解：把x＝1代入方程，得：﹣2﹣m＝0，
解得m＝﹣2．
故答案为：﹣2．
9．（3分）一天早晨的气温是﹣3℃，中午上升了11℃，半夜又下降了9℃，半夜的气温是 ﹣1 ℃．
【解答】解：半夜的气温是﹣3+11﹣9＝8﹣9＝﹣1℃，
故答案为：﹣1．
10．（3分）若﹣xay2与5x4y2是同类项，则常数a的值为 4 ．
【解答】解：∵﹣xay2与5x4y2是同类项，
∴a＝4．
故答案为：4．
11．（3分）已知a，b为有理数，且|a+1|+（2023﹣b）2＝0，则ab＝ ﹣1 ．
【解答】解：∵|a+1|+（2023﹣b）2＝0，
∴a+1＝0且2023﹣b＝0，
解得a＝﹣1，b＝2023，
∴ab＝（﹣1）2023＝﹣1．
故答案为：﹣1．
12．（3分）某市出租车的收费标准是：起步价为8元，起步里程为3km（3km以内按起步价付费），3km后每千米收2元．某人乘出租车从甲地到乙地共付费16元．设甲、乙两地之间的路程为x km，可得方程 8+2（x﹣3）＝16 ．
【解答】解：设甲、乙两地的路程为x km，
由16＞8可知x＞3，则超过3km的路程为（x﹣3）km，此段路程收的费用为2（x﹣3）元，某人乘出租车从甲地到乙地共付费为16元，
可得方程8+2（x﹣3）＝16，
故答案为：8+2（x﹣3）＝16，
13．（3分）代数式﹣2a+1与1+4a互为相反数，则a＝ ﹣1 ．
【解答】解：∵代数式﹣2a+1与1+4a互为相反数，
∴﹣2a+1+1+4a＝0，
解得a＝﹣1．
故答案为：﹣1．
14．（3分）若x2+x加上一个多项式的和是2x2+x+1，则这个多项式是 x2+1 ．
【解答】解：（2x2+x+1）﹣（x2+x）
＝2x2+x+1﹣x2﹣x
＝x2+1．
故答案为：x2+1．
15．（3分）有理数a，b在数轴上的位置如图：
则下列结论：①ab＜0；②a+b＞0；③b﹣a＞0；④|a﹣b|＝a﹣b； ⑤﹣3＜﹣b＜﹣2．其中结论正确的是 ①②③⑤ （填序号）．
【解答】解：从有理数a，b在数轴上的位置可知﹣2＜a＜﹣1，2＜b＜3，
根据异号两数相乘得负可判定出①正确；
根据有理数的加法法则：异号两数相加取绝对值较大加数的符号，故取b的符号，所以②正确；
根据有理数的减法法则：减去一个数等于加上它的相反数，可知b﹣a＞0，所以③正确；
因a﹣b＜0，根据绝对值的定义可知|a﹣b|＝b﹣a，故④错误；
因2＜b＜3，根据相反数的定义可得﹣3＜﹣b＜﹣2，所以⑤正确；
所以正确的有①②③⑤共4个．
故答案为：①②③⑤．
16．（3分）我国“华为”公司是世界通讯领域的龙头企业，某款手机后置摄像头模组如图所示．其中大圆的半径为r，中间小圆的半径为12r，4个半径为15r的高清圆形镜头分布在两圆之间．请用含r的代数式表示图中阴影部分的面积 59πr2100 ．
【解答】解：阴影面积：πr2﹣π（12r）2﹣π（15r）2×4
＝πr2-14πr2-425πr2
=59πr2100，
故答案为：59πr2100．
三、解答题（本大题共102分．请在答题纸指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（16分）计算：
（1）﹣3﹣8+5﹣7；
（2）34+(-12)-(-78)÷(-78)；
（3）-24×(-12+34-23)；
（4）-42÷(-3)3×(32)3-|13-3|．
【解答】解：（1）原式＝﹣11+5﹣7
＝﹣6﹣7
＝﹣13；
（2）原式=34-12-1
=-34；
（3）原式＝24×12-24×34+24×23
＝12﹣18+16
＝10；
（4）原式＝﹣16÷（﹣27）×278-83
＝16×127×278-83
＝2-83
=-23．
18．（8分）化简：
（1）﹣3x+2y﹣6x﹣9y；
（2）（5a+3b）﹣（2a﹣5b）．
【解答】解：（1）原式＝﹣9x﹣7y；
（2）原式＝5a+3b﹣2a+5b＝3a+8b．
19．（6分）解方程：-12x+1＝3+x．
【解答】解：-12x+1＝3+x，
-12x﹣x＝3﹣1，
-32x＝2，
x=-43．
20．（10分）先化简再求值：4a2+3（b2﹣2ab）﹣2（2a2﹣ab），其中a=-12，b=-3．
【解答】解：原式＝4a2+3b2﹣6ab﹣4a2+2ab
＝﹣4ab+3b2；
当a=-12，b＝﹣3时，
原式＝﹣4×（-12）×（﹣3）+3×（﹣3）2
＝﹣6+27
＝21．
21．（10分）请画数轴，并完成以下内容：
（1）在数轴上表示下列各数：0，﹣|+2|，-(-52)，72，π；
（2）把以上5个数用“＜”号连接起来．
【解答】解：（1）﹣|+2|＝﹣2，﹣（-52）=52=2.5，72=3.5，在数轴上表示如下：
（2）把这5个数用“＜”号连接起来为﹣|+2|＜0＜﹣（-52）＜π＜72．
22．（8分）电影《万里归途》成为了国庆假期市民观影的首选．某市9月30日该电影票的售票量为1.1万张，10月1日至10月7日售票量（单位，万张）的变化如下表（“+”表示售票量比前一天多，“﹣”表示售票量比前一天少）：
请根据以上信息，回答下列问题：
（1）10月2日的售票量为多少万张？
（2）10月7日与9月30日相比较，哪一天的售票量多？
（3）若平均每张票价为45元，则10月1日到10月7日某市《万里归途》的票房收入多少万元？
【解答】解：（1）10月2日的售票量为：1.1+0.5+0.1＝1.7（万张）；
答：10月2日的售票量为1.7万张；
（2）10月1日的售票量为：1.1+0.5＝1.6（万张）；
10月2日的售票量为：1.6+0.1＝1.7（万张）；
10月3日的售票量为：1.7﹣0.3＝1.4（万张）；
10月4日的售票量为：1.4﹣0.2＝1.2（万张）；
10月5日的售票量为：1.2+0.4＝1.6（万张）；
10月6日的售票量为：1.6﹣0.2＝1.4（万张）；
10月7日的售票量为：1.4+0.1＝1.5（万张）；
答：10月7日与9月30日相比较，10月7的售票量多；
（3）1.1×7+（0.5+0.6+0.3+0.1+0.5+0.3+0.4）
＝7.7+（1+1+0.7）
＝7.7+2.7
＝10.4（万张），
10.4×45＝468（万元），
答：票房收入468万元．
23．（10分）据了解，火车的票价是按“全程票价×实际里程数总里程数”的方法定价的．已知A站与H站之间的总里程数是1500千米，全程票价为600元．如图标出了列车各经停站相应的里程数．
（1）张叔叔从D站上车，到F站下车，票价应该是多少元？
（2）王叔叔从E站上车，票价为240元，请问他的目的地是哪个站？
【解答】（1）张叔叔从D站上车，到F站下车，票价应该是200元
（2）B站或者H站
【分析】（1）根据火车的票价＝“全程票价×实际里程数÷总里程数”进行求解即可；
（2）根据票价求出里程数即可得到答案．
【详解】（1）解：(1200-700)×6001500=200元，
答：张叔叔从D站上车，到F站下车，票价应该是200元；
（2）解：240÷6001500=600千米，
∴E站到目的地的距离为600千米，
∴目的地的站点是B站或者H站．
【点睛】本题主要考查了有理数四则混合计算的应用，有理数除法的应用，正确理解题意是解题的关键．
24．（10分）（1）在下列横线上用含有a，b的代数式表示相应图形的面积．
① a2 ② 2ab ③ b2 ④ （a+b）2
（2）请在图④画出拼图并通过拼图，你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表达： a2+2ab+b2＝（a+b）2 ．
（3）利用（2）的结论计算10.232+20.46×9.77+9.772的值．
【解答】解：（1）a2、2ab、b2、（a+b）2；
（2）a2+2ab+b2＝（a+b）2；
（3）10.232+20.46×9.77+9.772＝（19+1）2＝400．
故答案为：a2、2ab、b2、（a+b）2．
（2）a2+2ab+b2＝（a+b）2；
25．（12分）已知：A=32x2-xy+1，B=5x2+4xy-2，
（1）求2A﹣B（用含x、y的代数式表示）；
（2）若x2+3xy=34，求2A﹣B值．
【解答】解：（1）2A-B=2(32x2-xy+1)-(5x2+4xy-2)
＝3x2﹣2xy+2﹣5x2﹣4xy+2
＝﹣2x2﹣6xy+4．
（2）∵x2+3xy=34，
∴2x2+6xy=32，
∴原式=-(2x2+6xy)+4=-32+4=52．
26．（12分）【实际问题】
某商场在双十一期间为了鼓励消费，设计了抽奖活动，方案如下：根据不同的消费金额，每次抽奖时可以从100张面值分别为1元、2元、3元、…、100元的奖券中（面值为整数），一次任意抽取2张、3张、4张、…等若干张奖券，奖券的面值金额之和即为优惠金额．某顾客获得了一次抽取5张奖券的机会，小明想知道该顾客共有多少种不同的优惠金额？
【问题建模】
从1，2，3，…，n（n为整数，且n＞5）这n个整数中任取5个整数，这5个整数之和共有多少种不同的结果？
【模型探究】
我们采取一般问题特殊化的策略，先从最简单的情形入手，从中找出解决问题的方法．从1，2，3这3个整数中任取2个整数，这2个整数之和共有多少种不同的结果？
如表所示：所取的2个整数之和可以为3，4，5，也就是从3到5的连续整数，其中最小是3，最大是5，所以共有3种不同的结果．
（1）从1，2，3，4，5这5个整数中任取2个整数，这2个整数之和共有 7 种不同的结果．
（2）从1，2，3，…，n（n为整数，且n＞5）这n个整数中任取3个整数，这3个整数之和共有 （3n﹣8） 种不同的结果．
（3）归纳结论：从1，2，3，…，n（n为整数，且n＞5）这n个整数中任取5个整数，这5个整数之和共有 （5n﹣24） 种不同的结果．
【问题解决】
从100张面值分别为1元、2元、3元、…、100元的奖券中（面值为整数），一次任意抽取5张奖券，共有 476 种不同的优惠金额．
【问题拓展】
从3，4，5，…，n（n为整数，且n＞5）这n个整数中任取5个整数，使得取出的这些整数之和共有121种不同的结果，求n的值．（写出解答过程）
【解答】解：（1）从1，2，3，4，5这5个整数中任取2个整数，
则这2个整数之和最小值为：1+2＝3，最大值为：4+5＝9，
则这2个整数之和共有9﹣3+1＝7种不同情况，
故答案为：7；
（2）从1，2，3，……，n（n为整数，且n＞5）这n个整数中任取3个整数，
则这3个整数之和最小值为：1+2+3＝6，最大值为：n﹣2+n﹣1+n＝3n﹣3，
则这3个整数之和共有不同结果的种数为：3n﹣3﹣6+1＝（3n﹣8）种，
故答案为：（3n﹣8）；
（3）归纳总结：从1，2，3，……，n（n为整数，且n＞5）这n个整数中任取5个整数，
则这5个整数之和的最小值为：1+2+3+4+5＝15，最大值为n+（n﹣1）+（n﹣2）+（n﹣3）+（n﹣4）＝5n﹣10，
则这5个整数之和共有不同结果的种数为：5n﹣10﹣15+1＝（5n﹣24）种，
故答案为：（5n﹣24）；
问题解决：从100张面值分别为1元、2元、3元、……、100元的奖券中（面值为整数），一次任意抽取5张奖券，
则这5张奖券的和的最小值为：1+2+3+4+5＝15（元），最大值为：100+99+98+97+96＝490（元），
则这5张奖券的和共有不同优惠金额的种数为：490﹣15+1＝476（种），
故答案为：476；
问题拓展：从3，4，5，……，n（n为整数，且n＞5）这n个整数中任取5个整数，
则这5个整数之和的最小值为：3+4+5+6+7＝25，最大值为n+（n﹣1）+（n﹣2）+（n﹣3）+（n﹣4）＝5n﹣10，
则这5个整数之和共有不同结果的种数为：5n﹣10﹣25+1＝（5n﹣34）种，
∴5n﹣34＝121，
解得：n＝31．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/10/22 8:32:50；用户：15151889565；邮箱：15151889565；学号：23757877日期
1日
2日
3日
4日
5日
6日
7日
售票量的变化
+0.5
+0.1
﹣0.3
﹣0.2
+0.4
﹣0.2
+0.1
所取的2个整数
1，2
1，3
2，3
2个整数之和
3
4
5
日期
1日
2日
3日
4日
5日
6日
7日
售票量的变化
+0.5
+0.1
﹣0.3
﹣0.2
+0.4
﹣0.2
+0.1
所取的2个整数
1，2
1，3
2，3
2个整数之和
3
4
5