湖南省长沙市长沙明德中学2025届九年级数学第一学期开学联考模拟试题【含答案】

这是一份湖南省长沙市长沙明德中学2025届九年级数学第一学期开学联考模拟试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）为筹备班级联欢会，班干部对全班同学最爱吃的水果进行了统计，最终决定买哪种水果时，班干部最关心的统计量是( )
A．平均数B．中位数
C．众数D．方差
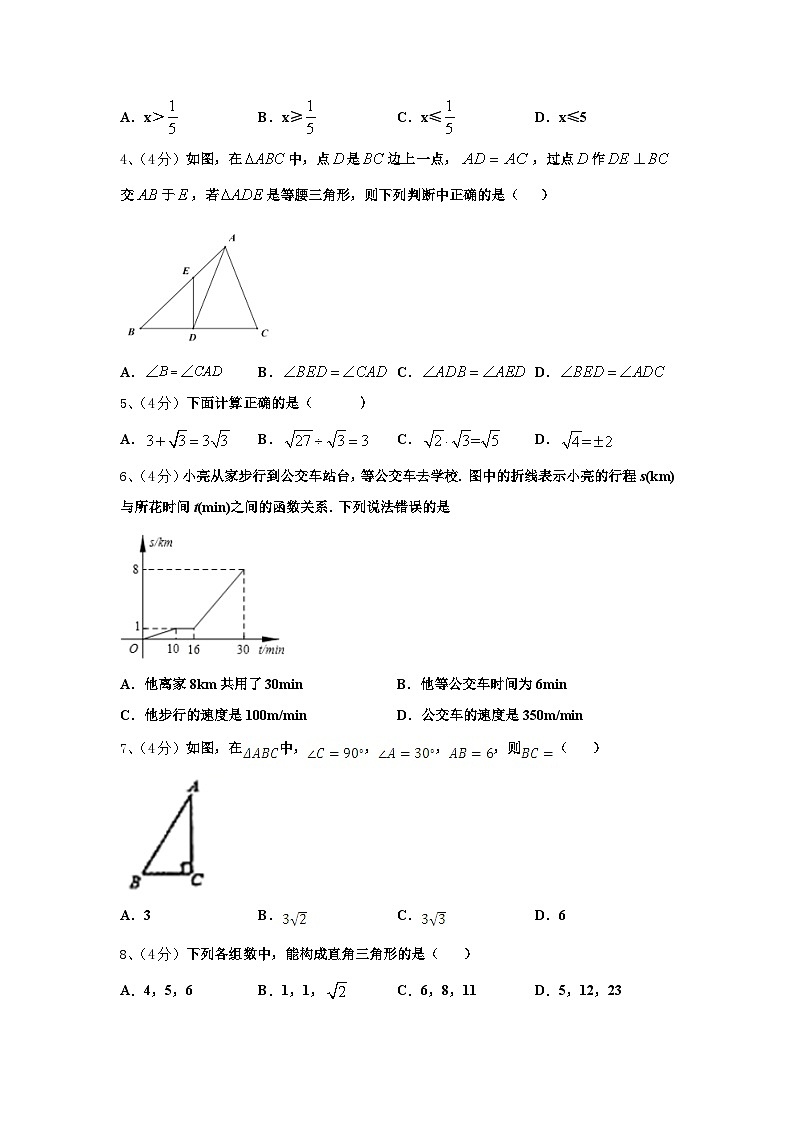
2、（4分）如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
下面有三个推断：
①当抛掷次数是100时，计算机记录“正面向上”的次数是47，所以“正面向上”的概率是0.47；
②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5；
③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率一定是0.1．
其中合理的是( )
A．①B．②C．①②D．①③
3、（4分）若二次根式有意义，则x的取值范围是( )
A．x＞B．x≥C．x≤D．x≤5
4、（4分）如图，在中，点是边上一点，，过点作交于，若是等腰三角形，则下列判断中正确的是（ ）
A．B．C．D．
5、（4分）下面计算正确的是（ ）
A．B．C．D．
6、（4分）小亮从家步行到公交车站台，等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是
A．他离家8km共用了30minB．他等公交车时间为6min
C．他步行的速度是100m/minD．公交车的速度是350m/min
7、（4分）如图，在中，，，，则（ ）
A．3B．C．D．6
8、（4分）下列各组数中，能构成直角三角形的是（ ）
A．4，5，6B．1，1，C．6，8，11D．5，12，23
二、填空题（本大题共5个小题，每小题4分，共20分）
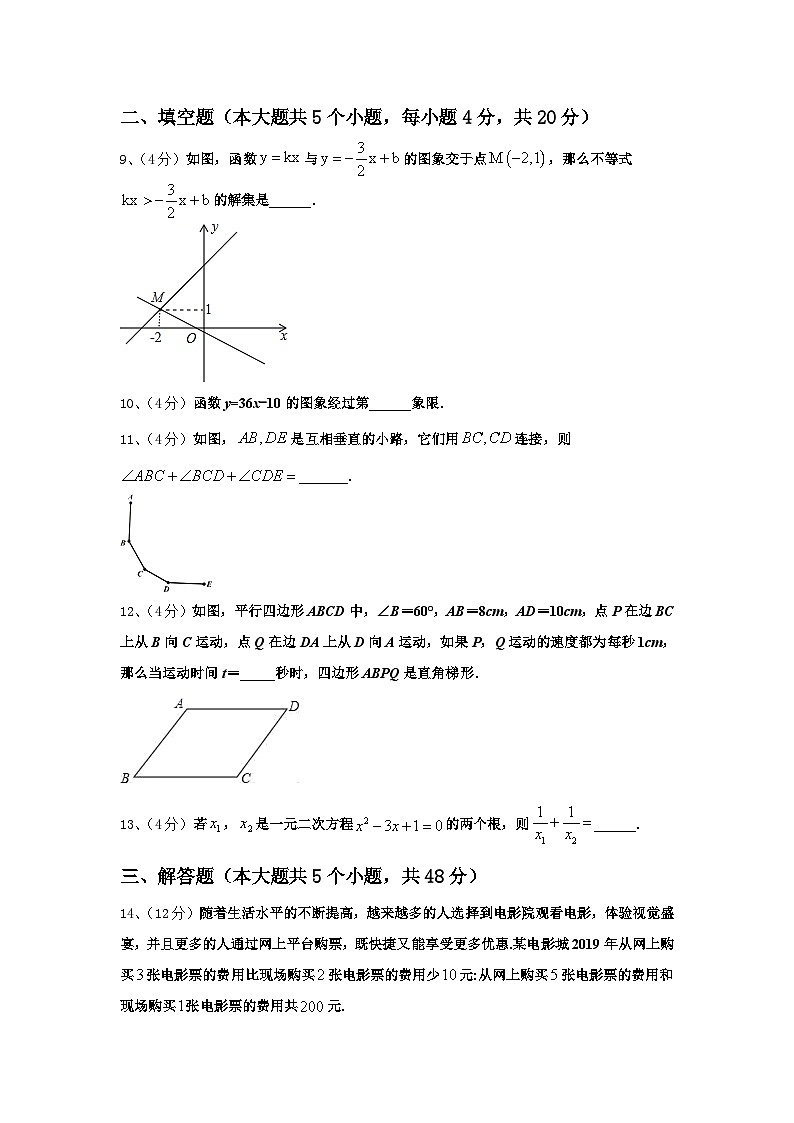
9、（4分）如图，函数与的图象交于点，那么不等式的解集是______．
10、（4分）函数y=36x-10的图象经过第______象限．
11、（4分）如图，是互相垂直的小路，它们用连接，则_______.
12、（4分）如图，平行四边形ABCD中，∠B＝60°，AB＝8cm，AD＝10cm，点P在边BC上从B向C运动，点Q在边DA上从D向A运动，如果P，Q运动的速度都为每秒1cm，那么当运动时间t＝_____秒时，四边形ABPQ是直角梯形．
13、（4分）若，是一元二次方程的两个根，则______.
三、解答题（本大题共5个小题，共48分）
14、（12分）随着生活水平的不断提高，越来越多的人选择到电影院观看电影，体验视觉盛宴，并且更多的人通过网上平台购票，既快捷又能享受更多优惠.某电影城2019年从网上购买张电影票的费用比现场购买张电影票的费用少元:从网上购买张电影票的费用和现场购买张电影票的费用共元.
（1）求该电影城2019年在网上购票和现场购票每张电影票的价格为多少元?
（2）2019年五一当天，该电影城按照2019年网上购票和现场购票的价格销售电影票，当天售出的总票数为张.五一假期过后，观影人数出现下降，于是电影城决定从5月5日开始调整票价：现场购票价格下调，网上购票价格不变，结果发现，现场购票每张电影票的价格每降低元，售出总票数就比五一当天增加张.经统计，5月5日售出的总票数中有的电影票通过网上售出，其余通过现场售出，且当天票房总收入为元，试求出5月5日当天现场购票每张电影票的价格为多少元?
15、（8分）地铁检票处有三个进站闸口A、B、C.
①人选择A进站闸口通过的概率是________；
②两个人选择不同进站闸口通过的概率.（用树状图或列表法求解）
16、（8分）如图，正方形ABCD中，O是对角线AC、BD的交点，过点O作OE⊥OF，分别交AB、BC于E. F.
(1)求证：△OEF是等腰直角三角形。
(2)若AE=4，CF=3，求EF的长。
17、（10分）在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：
（1）参加比赛有_____名运动员，图①中a的值是_____,补全条形统计图.
（2）统计的这组初赛成绩数据的众数是_____，中位数是_____，平均数是_____.
（3）根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛.
18、（10分）已知：如图，是的角平分线，于点 ，于点，，求证：是的中垂线．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）已知：如图，正方形ABCD中，对角线AC和BD相交于点O．E、F分别是边AD、CD上的点，若AE＝4cm，CF＝3cm，且OE⊥OF，则EF的长为_____cm．
20、（4分）若m＝+5，则mn＝___．
21、（4分）如图，在长20米、宽10米的长方形草地内修建了宽2米的道路，则草地的面积是______平方米．
22、（4分）若关于的两个方程与有一个解相同，则__________．
23、（4分）直角中，，、、分别为、、的中点，已知，则________．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，一次函数的图像经过点A（-1,0），并与反比例函数（）的图像交于B（m,4）
（1）求的值；
（2）以AB为一边，在AB的左侧作正方形，求C点坐标；
（3）将正方形沿着轴的正方向，向右平移n个单位长度，得到正方形,线段的中点为点,若点和点同时落在反比例函数的图像上，求n的值.
25、（10分）先化简，再求值：，其中x=20160+4
26、（12分）如图，抛物线y＝ax2+bx﹣3过A（1，0），B（﹣3，0），直线AD交抛物线于点D，点D的横坐标为﹣2，点P（m，n）是线段AD上的动点．
（1）求直线AD及抛物线的解析式；
（2）过点P的直线垂直于x轴，交抛物线于点Q，求线段PQ的长度l与m的关系式，m为何值时，PQ最长？
（3）在平面内是否存在整点（横、纵坐标都为整数）R，使得P，Q，D，R为顶点的四边形是平行四边形？若存在，直接写出点R的坐标；若不存在，说明理由．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
分析：一组数据中出现次数最多的一个数是这组数据的众数，班长最关心吃哪种水果的人最多，即这组数据的众数．
详解：吃哪种水果的人最多，就决定最终买哪种水果，而一组数据中出现次数最多的一个数是这组数据的众数．
故选C．
点睛：此题主要考查统计的有关知识，主要是众数的意义．反映数据集中程度的统计量有平均数、中位数、众数方差等，各有局限性，因此要对统计量进行合理的选择和恰当的运用．
2、B
【解析】
随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5，据此进行判断即可．
【详解】
解：①当抛掷次数是100时，计算机记录“正面向上”的次数是47，“正面向上”的概率不一定是0.47，故错误；
②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5，故正确；
③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率不一定是0.1，故错误．
故选：B．
本题考查了利用频率估计概率，明确概率的定义是解题的关键．
3、B
【解析】
根据二次根式有意义的条件列出不等式，解不等式即可．
【详解】
解：由题意得，5x﹣1≥0，
解得，x≥，
故选B．
本题考查的是二次根式有意义的条件，掌握二次根式中的被开方数是非负数是解题的关键．
4、B
【解析】
根据等腰三角形的性质得到根据垂直的性质得到
根据等量代换得到又即可得到
根据同角的余角相等即可得到.
【详解】
,

,

从而
是等腰三角形，


，
故选：B.
考查等腰三角形的性质，垂直的性质，三角形的内角和定理，掌握同角的余角相等是解题的关键.
5、B
【解析】
分析：A．根据合并二次根式的法则即可判定；
B．根据二次根式的除法法则即可判定；
C．根据二次根式的乘法法则即可判定；
D．根据二次根式的性质即可判定．
详解：A．不是同类二次根式，不能合并．故选项错误；
B．÷==1．故选项正确；
C．．故选项错误；
D．=2． 故选项错误．
故选B．
点睛：本题考查了二次根式的计算，要掌握各运算法则．二次根式的加减运算，只有同类二次根式才能合并；乘法法则；除法法则．
6、D
【解析】
A、依题意得他离家8km共用了30min，故选项正确；
B、依题意在第10min开始等公交车，第16min结束，故他等公交车时间为6min，故选项正确；
C、他步行10min走了1000m，故他步行的速度为他步行的速度是100m/min，故选项正确；
D、公交车（30-16）min走了（8-1）km，故公交车的速度为7000÷14=500m/min，故选项错误．
故选D．
7、A
【解析】
根据直角三角形的性质：30度的锐角所对的直角边等于斜边的一半即可求解．
【详解】
解：∵在△ABC中，∠C=90°，∠A=30°，
∴BC= AB= ×6=3，
故选：A．
本题考查了含30度的直角三角形的性质，正确掌握定理是解题的关键．
8、B
【解析】
根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个是直角三角形判定则可．
【详解】
解：A、，故不是直角三角形，错误；
B、 ，故是直角三角形，正确；
C、 故不是直角三角形，错误；
D、故不是直角三角形，错误．
故选：B．
本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
函数与的图象的交点由图象可直接得到答案，以交点为分界，交点左边，结合图象可得答案．
【详解】
解：由图象可得：函数与的图象交于点，
关于x的不等式的解集是.
故答案为：.
此题主要考查了一次函数与一元一次不等式的关系，关键是正确从图象中得到信息，掌握数形结合思想的应用．
10、【解析】
根据y＝kx＋b（k≠0，且k，b为常数），当k＞0，b＜0时，函数图象过一、三、四象限．
【详解】
解：因为函数中，
，，
所以函数图象过一、三、四象限，
故答案为：一、三、四．
此题主要考查了一次函数的性质，同学们应熟练掌握根据函数式判断出函数图象的位置，这是考查重点内容之一．
11、450°
【解析】
如图，作出六边形，根据“n边形的内角和是（n-2）•180°”求出内角和，再求∠的度数．
【详解】
解：过点A作AB的垂线，过点E作DE的垂线，两线相交于点Q，
则∠BAQ=∠DEQ=90°，
∵DE⊥AB，QA⊥AB，
∴DE∥QA，
∴∠AQE=180°-∠DEQ=90°，
∵六边形ABCDEQ的内角和为：（6-2）•180°=720°，
∴=720°-90°×3=450°．
故答案为：450°．
本题主要考查了多边形的内角和定理．解决本题的关键是正确运用多边形的内角和公式，是需要熟记的内容．
12、1
【解析】
过点A作AE⊥BC于E，因为AD∥BC，所以当AE∥QP时，则四边形ABPQ是直角梯形，利用已知条件和路程与速度的关系式即可求出时间t的值
【详解】
解：
∵四边形ABCD是平行四边形，
∴AD∥BC，
过点A作AE⊥BC于E，
∴当AE∥QP时，则四边形ABPQ是直角梯形，
∵∠B＝60°，AB＝8cm，
∴BE＝4cm，
∵P，Q运动的速度都为每秒1cm，
∴AQ＝10﹣t，AP＝t，
∵BE＝4，
∴EP＝t﹣4，
∵AE⊥BC，AQ∥EP，AE∥QP，
∴QP⊥BC，AQ⊥AD，
∴四边形AEPQ是矩形，
∴AQ＝EP，
即10﹣t＝t﹣4，
解得t＝1，
故答案为：1．
此题考查直角梯形，平行四边形的性质，解题关键在于作辅助线
13、3
【解析】
利用根与系数的关系可得两根之和与两根之积，再整体代入通分后的式子计算即可.
【详解】
解：∵，是一元二次方程的两个根，∴，
∴.
故答案为：3.
本题考查的是一元二次方程根与系数的关系，熟练掌握基本知识是解题的关键.
三、解答题（本大题共5个小题，共48分）
14、（1）网上购票价格30元，现场购票价格50元；（2）5月5日当天现场购票每张电影票的价格为40元，见解析.
【解析】
（1）首先设网上每张电影票价格为元，现场每张电影票价格为元，然后根据题意，列出关系式，即可得解；
（2）首先设现场购票每张电影票的价格下降元，然后根据题意列出关系式，即可得解.
【详解】
（1）设网上每张电影票价格为元，现场每张电影票价格为元.
解得：
答：网上购票价格30元，现场购票价格50元.
（2）设现场购票每张电影票的价格下降元
解得（舍去），
答：5月5日当天现场购票每张电影票的价格为40元.
此题主要考查二元一次方程组、一元一次方程的实际应用，关键是根据题意列出关系式，即可解题.
15、（1）；（2）
【解析】
（1）直接利用概率公式计算可得；
（2）画树状图展示所有9种等可能的结果数，再找出选择不同通道通过的结果数，然后根据概率公式求解．
【详解】
解：（1）选择A通道通过的概率是；
故答案为：
（2）画树形图如下；
由图中可知，共有9种等可能情况，其中选择不同通道通过的有6种结果，
所以选择不同通道通过的概率为
本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式求事件A或B的概率．
16、（1）见解析；（2）5.
【解析】
（1）根据正方形的性质可得∠ABO=∠ACF=45°，OB=OC，∠BOC=90°，再根据同角的余角相等求出∠EOB=∠FOC，然后利用“角边角”证明△BEO和△CFO全等，根据全等三角形对应边相等可得OE=OF，从而得证；
（2）根据全等三角形对应边相等可得BE=CF，再根据正方形的四条边都相等求出AE=BF，再利用勾股定理列式进行计算即可得解．
【详解】
(1)证明：∵四边形ABCD为正方形，
∴∠ABO=∠ACF=45∘,OB=OC,∠BOC=90∘，
∴∠FOC+∠BOF=90∘，
又∵OE⊥OF，
∴∠EOF=90∘，
∴∠EOB+∠BOF=90∘，
∴∠EOB=∠FOC，
在△BEO和△CFO中,
，
∴△BEO≌△CFO(ASA)，
∴OE=OF，
又∵∠EOF=90∘，
∴△DEF是等腰直角三角形；
(2)解∵△BEO≌△CFO(已证)，
∴BE=CF=3，
又∵四边形ABCD是正方形，
∴AB=BC，
∴AB−BE=BC−CF，
即AE=BF=4，
在Rt△BEF中,EF= = =5.
此题考查全等三角形的判定与性质，正方形的性质，解题关键在于得到∠ABO=∠ACF=45°，OB=OC，∠BOC=90°
17、（1）20，25，图详见解析；（2）众数：1.65m，中位数1.60m，平均数1.61m；（3）能.
【解析】
（1） 用整体1减去其他百分比，即可求出a的值，用已知人数除以所占百分比即可求解.
（2） 根据平均数，众数和中位数的定义分别进行求解.
（3） 根据中位数的意义可直接判断出能否进入复赛.
【详解】
（1），
（2）平均数；在这组数据样本中，1.65出现了6次，出现次数最多，故众数为1.65；将这组样本数据从小到大的顺序排列，其中处于中间的两个数都为1.60，所以中位数为.
（3）能.
本题主要考查数据的处理、数据的分析以及统计图表，熟悉掌握是关键.
18、见解析.
【解析】
由AD是△ABC的角平分线，DE⊥AB，DF⊥AC，根据角平分线的性质，可得DE=DF，∠BED=∠CFD=90°，继而证得Rt△BED≌Rt△CFD，则可得∠B=∠C，证得AB=AC，然后由三线合一，证得AD是BC的中垂线.
【详解】
解：是的角平分线，，，
，，
在和中，
，
，
，
，
是的角平分线，
是的中垂线.
此题考查了等腰三角形的性质与判定以及全等三角形的判定与性质．注意掌握三线合一性质的应用.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1
【解析】
试题解析：连接EF，
∵OD=OC，
∵OE⊥OF
∴∠EOD+∠FOD=90°
∵正方形ABCD
∴∠COF+∠DOF=90°
∴∠EOD=∠FOC
而∠ODE=∠OCF=41°
∴△OFC≌△OED，
∴OE=OF，CF=DE=3cm，则AE=DF=4，
根据勾股定理得到EF==1cm．
故答案为1．
20、1．
【解析】
直接利用二次根式有意义的条件得出m，n的值进而得出答案．
【详解】
∵m＝+5，
∴n＝2，则m＝5，
故mn＝1．
故答案为：1．
此题主要考查了二次根式有意义的条件，正确得出m，n的值是解题关键．
21、144米1．
【解析】
将道路分别向左、向上平移，得到草地为一个长方形，分别求出长方形的长和宽，再用长和宽相乘即可．
【详解】
解：将道路分别向左、向上平移，得到草地为一个长方形，
长方形的长为10-1=18（米），宽为10-1=8（米），
则草地面积为18×8=144米1．
故答案为：144米1．
本题考查了平移在生活中的运用，将道路分别向左、向上平移，得到草地为一个长方形是解题的关键．
22、1
【解析】
首先解出一元二次方程的解，根据两个方程的解相同，把x的值代入第二个方程中，解出a即可．
【详解】
解：解方程得x1＝2，x2＝−1，
∵x＋1≠0，
∴x≠−1，
把x＝2代入中得：，
解得：a＝1，
故答案为1．
此题主要考查了解一元二次方程，以及解分式方程，关键是正确确定x的值，分式方程注意分母要有意义．
23、3
【解析】
由三角形中位线定理得到DF=BC；然后根据直角三角形斜边上的中线等于斜边的一半得到AE=BC，则DF=AE．
【详解】
∵在直角△ABC中,∠BAC=90°，D. F分别为AB、AC的中点，
∴DF是△ABC的中位线，
∴DF=BC.
又∵点E是直角△ABC斜边BC的中点，
∴AE=BC，
∵DF=3，
∴DF=AE=3.
故答案为3.
本题考查了三角形中位线定理和直角三角形斜边上的中线．熟记定理是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、（1）k1=4；（2）C点坐标为（-3，6）；（3）n=.
【解析】
（1）把A点坐标代入y=2x+b，可求出b值，把B（m，4）代入可求出m值，代入即可求出k1的值；（2）过B作BF⊥x轴于F，过C作CG⊥FB，交FB的延长线于G，利用AAS可证明△CBG≌△BAF，可得AF=BG，CG=BF，根据A、B两点坐标即可得C点坐标；（3）由A、B、C三点坐标可得向右平移n个单位后A1、B1、C1的坐标，即可得E点坐标，根据k2=xy列方程即可求出n值.
【详解】
（1）∵一次函数的图像经过点A（-1，0），
∴-2+b=0，
解得：b=2，
∵点B（m，4）在一次函数y=2x+2上，
∴4=2m+2，
解得：m=1，
∵B（1，4）在反比例函数图象上，
∴k1=4.
（2）如图，过B作BF⊥x轴于F，过C作CG⊥FB，交FB的延长线于G，
∵A（-1，0），B（1，4），
∴AF=2，BF=4，
∴∠GCB+∠CBG=90°，
∵四边形ABCD是正方形，
∴∠ABC=90°，
∴∠ABF+∠CBG=90°，
∴∠GCB=∠ABF，
又∵BC=AB，∠AFB=∠CGB=90°，
∴△CBG≌△BAF，
∴BG=AF=2，CG=BF=4，
∴GF=6，
∵在AB的左侧作正方形ABCD，
∴C点坐标为（-3，6）.
（3）∵正方形ABCD沿x轴的正方向，向右平移n个单位长度，
∴A1（-1+n，0），B1（1+n，4），C1（-3+n，6），
∵线段A1B1的中点为点E，
∴E（n，2），
∵点和点E同时落在反比例函数的图像上，
∴k2=2n=6(-3+n)
解得：n=.
本题考查一次函数与反比例函数综合，涉及的知识点有平移的性质、全等三角形的性质，一次函数和反比例函数图象上点的坐标特征及正方形的性质，熟练掌握性质和定理是解题关键.
25、，.
【解析】
先算括号里面的，再算除法，最后求出x的值代入进行计算即可．
【详解】
解：原式，
∵x=20160+4=5，
∴原式=.
本题考查的是分式的化简求值，熟练掌握运算法则是解题关键．
26、（1）y＝x2+2x﹣1；（2）当m＝-时，PQ最长，最大值为；（1）R1（﹣2，﹣2），R2（﹣2，﹣4），R1（﹣2，﹣1），R4（﹣2，﹣5），R5（0，﹣1）．
【解析】
（1)根据待定系数法，可得抛物线的解析式；根据自变量与函数值的对应关系，可得D点坐标，再根据待定系数法，可得直线的解析式；
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得二次函数，根据二次函数的性质，可得答案；
(1)根据PQ的长是正整数，可得PQ，根据平行四边形的性质，对边平行且相等，可得DR的长，根据点的坐标表示方法，可得答案
【详解】
解：（1）将A（1，0），B（﹣1，0）代入y＝ax2+bx﹣1得：
解得：
∴抛物线的解析式为：y＝x2+2x﹣1，
当x＝﹣2时，y＝（﹣2）2﹣4﹣1＝﹣1，
∴D（﹣2，﹣1），
设直线AD的解析式为y＝kx+b，将A（1，0），D（﹣2，﹣1）代入得：
解得：
∴直线AD的解析式为y＝x﹣1；
因此直线AD的解析式为y＝x﹣1，抛物线的解析式为：y＝x2+2x﹣1．
（2）∵点P在直线AD上，Q抛物线上，P（m，n），
∴n＝m﹣1 Q（m，m2+2m﹣1）
∴PQ的长l＝（m﹣1）﹣（m2+2m﹣1）＝﹣m2﹣m+2 （﹣2≤m≤1）
∴当m＝ 时，PQ的长l最大＝﹣（ ）2﹣（）+2＝ ．
答：线段PQ的长度l与m的关系式为：l＝﹣m2﹣m+2 （﹣2≤m≤1）
当m＝时，PQ最长，最大值为．
（1）①若PQ为平行四边形的一边，则R一定在直线x＝﹣2上，如图：
∵PQ的长为0＜PQ≤的整数，
∴PQ＝1或PQ＝2，
当PQ＝1时，则DR＝1，此时，在点D上方有R1（﹣2，﹣2），在点D下方有R2（﹣2，﹣4）；
当PQ＝2时，则DR＝2，此时，在点D上方有R1（﹣2，﹣1），在点D下方有R4（﹣2，﹣5）；
②若PQ为平行四边形的一条对角线，则PQ与DR互相平分，此时R与点C重合，即R5（0，﹣1）
综上所述，符合条件的点R有：R1（﹣2，﹣2），R2（﹣2，﹣4），R1（﹣2，﹣1），R4（﹣2，﹣5），R5（0，﹣1）．
答：符合条件的点R共有5个，即：R1（﹣2，﹣2），R2（﹣2，﹣4），R1（﹣2，﹣1），R4（﹣2，﹣5），R5（0，﹣1）．
此题考查一元二次方程-用待定系数法求解析式，二次函数的性质，平行四边形的性质，解题关键在于把已知点代入解析式
题号
一
二
三
四
五
总分
得分
批阅人