数学九年级上册第3章 圆的基本性质3.5 圆周角教案配套课件ppt

这是一份数学九年级上册第3章 圆的基本性质3.5 圆周角教案配套课件ppt，共21页。PPT课件主要包含了圆周角定理等内容，欢迎下载使用。
认识圆周角，掌握圆周角定理和它的推论.会用圆周角定理和它的推论进行简单的计算证明.在证明圆周角定理的过程中体会分类讨论的思想.
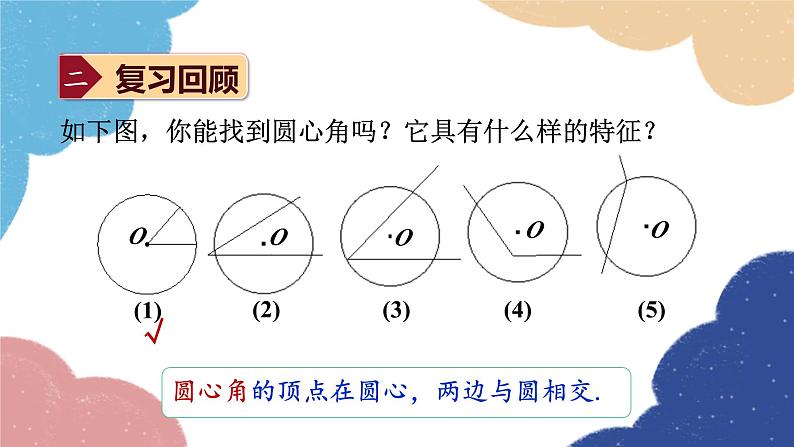
如下图，你能找到圆心角吗？它具有什么样的特征？
圆心角的顶点在圆心，两边与圆相交.
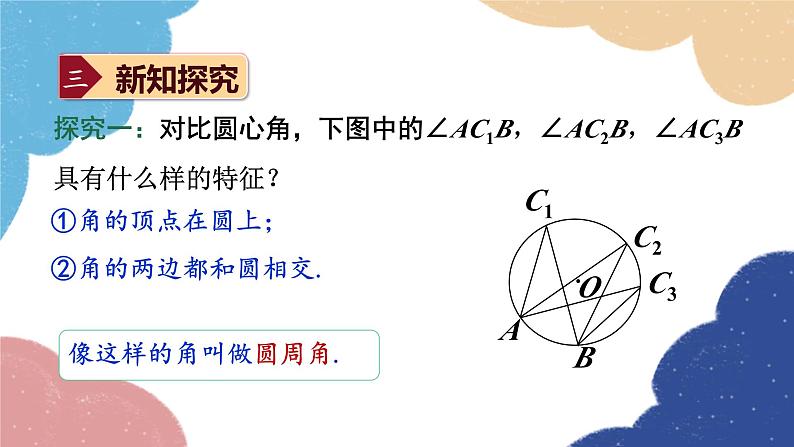
探究一：对比圆心角，下图中的∠AC1B，∠AC2B，∠AC3B 具有什么样的特征？
像这样的角叫做圆周角.
①角的顶点在圆上；②角的两边都和圆相交.
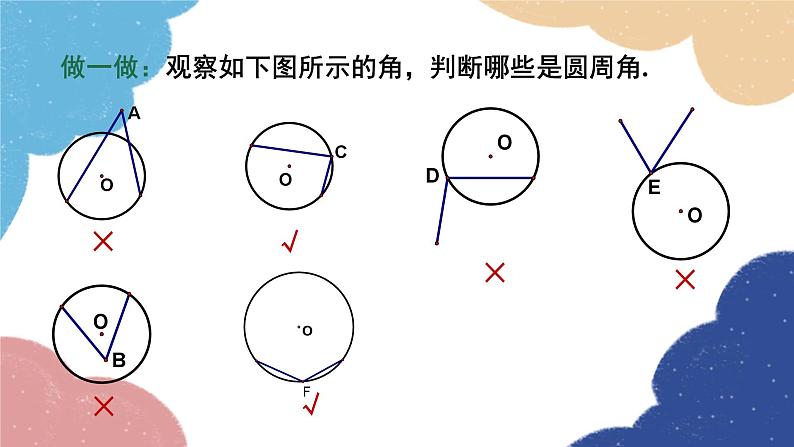
做一做：观察如下图所示的角，判断哪些是圆周角.
探究二：动手做一做任意画一个圆，在圆上任取弧AB，并任意画出其所对的两个圆周角及一个圆心角.1.分别量出弧AB所对的圆周角和圆心角的度数，圆周角和圆心角之间有什么关系？2.比较弧AB所对的两个圆周角的度数. 再变动点C在圆周上的位置，圆周角的度数有没有变化. 你发现其中有什么规律吗？  
1.圆周角的度数等于它所对弧上的圆心角度数的一半.2.两个圆周角的度数相等.变动点C在圆周上的位置，圆周角的度数无变化，即同一条弧所对的圆周角相等.
这个结论是否适用于所有情况呢？
分析：由于圆心有在圆周角内、圆周角外和圆周角的一条边上三类情况，因此需分别对三类不同情况给出证明.
证明：(1)当圆心O在∠BAC的一边AB上时，如图，
(2)当圆心O在∠BAC的内部时，如图，
连结AO并延长，交⊙O于点D.利用(1)的结果，有
(3)当圆心O在∠BAC的外部时，如图，
圆周角的度数等于它所对弧上的圆心角度数的一半.
探究三：如图，若AB是⊙O的直径，那么，∠ACB=____.
反之，若∠ACB是直角，则∠AOB=_____，
所以点A，O，B在一条直线上，AB是⊙O的_______.
由此我们得到圆周角定理的一个推论：
半圆(或直径)所对的圆周角是直角.
90°的圆周角所对的弦是直径.
例1 如图，等腰三角形ABC的顶角∠BAC为50°，以腰AB为直径作半圆，交BC于点D，交AC于点E.求弧BD，弧DE，弧AE的度数.
解：连结BE，AD. ∵AB是圆的直径， ∴∠AEB=∠ADB=90°.∵∠BAC=50°，∴∠ABE=90°-∠BAC=90°-50°=40°.
又∵△ABC是等腰三角形，
2.使用曲尺检验工件的凹面，成半圆时为合格．如图所示的三种情况中，哪种是合格的？哪种是不合格的？为什么？
解：第三种合格，第一种和第二种不合格．因为半圆（或直径）所对的圆周角是直角，所以第三个凹面为半圆．
3.在圆中，一条弧所对的圆心角和圆周角分别为(2x＋100)°和(5x－30)°，求这条弧所对的圆心角和圆周角的度数.
解：根据圆周角定理知：(2x+100)°=2×(5x-30)°，解得：x=20.则2x+100=140，5x-30=70.答：这条弧所对的圆心角和圆周角的度数分别为140 °，70 °.
4.只给你一把三角尺，你能找出一个圆（如图）的圆心吗？试一试.
解：因为①90°的圆周角所对的弦是直径；②同一圆中两条不重合的直径的交点是圆心. 则可用三角尺找出圆的两条直径，它们的交点就是圆心O.
角的顶点在圆上，角的两边都和圆相交，这样的角叫做圆周角.
半圆(或直径)所对的圆周角是直角.90°的圆周角所对的弦是直径.
本节课学习了哪些知识？