内蒙古赤峰市松山区2023-2024学年七年级上学期期中考试数学试卷(含解析)

这是一份内蒙古赤峰市松山区2023-2024学年七年级上学期期中考试数学试卷(含解析)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
七年级数学
（时间：90分钟，满分：100分）
一、选择题（本大题有12个小题，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．某中学积极响应“双减”政策，开展丰富多彩的课余活动，购买了一批足球，如图，张老师检测了4个足球，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数，从轻重的角度看，最接近标准质量的是（ ）
A．B．C．D．
2．用四舍五入法按要求对分别取近似值，其中错误的是（ ）
A．（精确到）B．（精确到千分位）
C．（精确到百分位）D．（精确到）
3．设P、Q都是关于x的4次多项式，关于P与Q的和，说法正确的是（ ）
A．8次多项式B．4次多项式C．次数可能大于4D．次数不大于4
4．2021年松山区GTP总值达到亿元，位居赤峰市第二位，其中亿用科学记数法表示为（ ）
A．B．C．D．
5．赤峰市某天的最高气温是，最低气温是，这一天的最高气温与最低气温的差是（ ）
A．B．C．D．
6．数轴上表示的点到某点的距离为，则该点表示的数是（ ）
A．B．C．或D．或
7．飞机无风时的航速为，风速为，则飞机顺风飞行的行程可表示为（ ）
A． B． C． D．
8．有理数，在数轴上的位置如图所示，下列各式正确的是（ ）

A．0B．C．D．
9．已知代数式的值为9，则的值为（ ）
A．18B．11C．10D．9
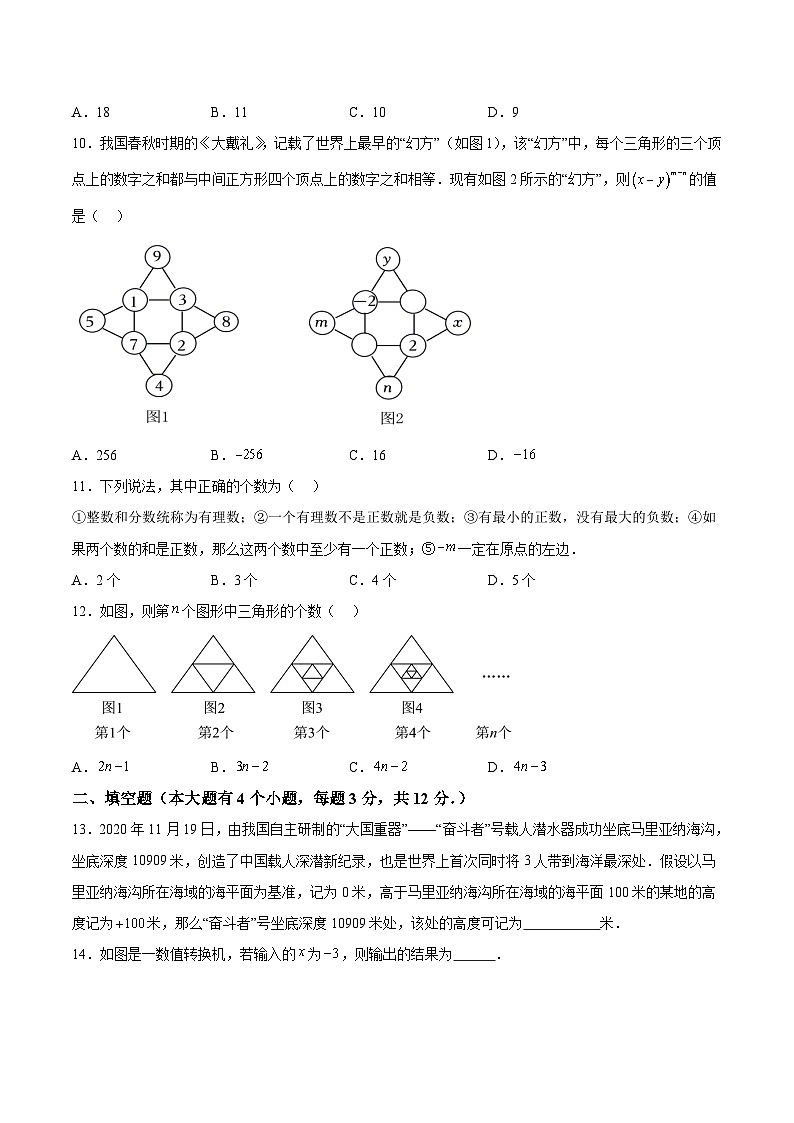
10．我国春秋时期的《大戴礼》，记载了世界上最早的“幻方”（如图1），该“幻方”中，每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等．现有如图2所示的“幻方”，则的值是（ ）
A．256B．C．16D．
11．下列说法，其中正确的个数为（ ）
①整数和分数统称为有理数；②一个有理数不是正数就是负数；③有最小的正数，没有最大的负数；④如果两个数的和是正数，那么这两个数中至少有一个正数；⑤一定在原点的左边．
A．2个B．3个C．4个D．5个
12．如图，则第个图形中三角形的个数（ ）
A．B．C．D．
二、填空题（本大题有4个小题，每题3分，共12分．）
13．2020年11月19日，由我国自主研制的“大国重器”——“奋斗者”号载人潜水器成功坐底马里亚纳海沟，坐底深度10909米，创造了中国载人深潜新纪录，也是世界上首次同时将3人带到海洋最深处．假设以马里亚纳海沟所在海域的海平面为基准，记为0米，高于马里亚纳海沟所在海域的海平面100米的某地的高度记为米，那么“奋斗者”号坐底深度10909米处，该处的高度可记为 米．
14．如图是一数值转换机，若输入的为，则输出的结果为 ．

15．如果a、b互为相反数，c、d互为负倒数，n为最大的负整数，m是绝对值最小的有理数，则代数式 ．
16．一组按规律排列的式子：则第n个式子是 ．
三、解答题（本大题共7小题，共52分．解答应写出文字说明、证明过程或演算步骤．）
17．计算：
18．先化简，再求值：，其中．
19．某环卫清扫车在一条南北大道上来回清扫大街，一天早晨，清扫车从岗亭出发，中午停留在环卫驿站，规定向北方向为正，当天上午连续行驶情况记录如下（单位：千米）：，，，，，，，．
(1)环卫驿站在岗亭何方？距离岗亭多远？在给定的数轴上标示出环卫驿站和岗亭的位置
(2)在清扫过程中，该车离开岗亭最远的距离是多少千米？（计算或用数轴表示均可）
(3)若清扫车每行驶千米耗油升，上午共耗油多少升？
20．赤峰市已经是水资匮乏城市，从2015年4月起赤峰市实行自来水阶梯水价，收费标准如下表所示：
(1)某用户12月份用水量为8吨，则该用户本月应缴水费是多少？
(2)若某用户的月用水量为m吨，请用含m的式子表示该用户月所缴水费．
(3)结合此题，请你用简单的语言对本市居民发出倡议．
21．小马虎做一道数学题，“已知两个多项式，，试求.”其中多项式的二次项系数印刷不清楚.
（1）小马虎看答案以后知道，请你替小马虎求出系数“”；
（2）在（1）的基础上，小马虎已经将多项式正确求出，老师又给出了一个多项式，要求小马虎求出的结果.小马虎在求解时，误把“”看成“”，结果求出的答案为.请你替小马虎求出“”的正确答案.
22．“双节”期间，王老师计划组织朋友去乌兰布统游览两日“草原秋景”，经了解，有甲、乙两家旅行社针对组团两日游的游客报价均为每人元，且提供的服务完全相同．甲旅行社表示，每人都按八五折收费；乙旅行社表示，若人数不超过人，每人都按九折收费，超过人，则超出部分每人按八折收费．假设组团参加甲，乙两家旅行社两日游的人数均为人．
(1)请列式表示甲、乙两家旅行社收取组团两日游的总费用；
(2)若王老师组团参加两日游的人数共有人，请你通过计算，在甲、乙两家旅行社中，帮助王老师选择收取总费用较少的一家．
23．阅读下面材料并回答问题．
(1)点A、B在数轴上分别表示数a、b，A、B两点之间的距离表示为．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，；当A、B两点都不在原点时，
①如图2，点A、B都在原点的右边，；
②如图3，点A、B都在原点的左边，；
③如图4，点A、B在原点的两边，．
综上，数轴上A、B两点之间的距离＝______．
(2)回答下列问题：
①数轴上表示2和5的两点之间的距离是______，数轴上表示﹣2和﹣5的两点之间的距离是______，数轴上表示1和﹣3的两点之间的距离是______；
②数轴上表示x和﹣1的两点A和B之间的距离是______，如果＝2，那么x为______．
③当式子取最小值时，相应的x的取值范围是______，最小值是______．
参考答案与解析
1．A
解析：解：∵，不足或超过的部分的绝对值越小越接近标准，
∴最接近标准质量的是选项A．
故选A．
2．B
解析：解：、（精确到），本选项正确，故不符合题意；
、（精确到千分位），而不是，本选项错误，故符合题意；
、（精确到百分位），本选项正确，故不符合题意；
、（精确到），本选项正确，故不符合题意．
故选：．
3．D
解析：∵P，Q最高项的次数都为4，
∴若P，Q最高次项是同类项，且系数互为相反数时，四次项合并为零，此时和的最高项的次数就低于4次，其它情况最高次项不能合并时和的次数仍为4次，
∴P与Q的和的次数不大于4．
故选：D
4．B
解析：解：亿，
故选：B．
5．D
解析：解：由题意得：；
故选D．
6．C
解析：解：在数轴上与表示的点距离是个单位长度的点所表示的数是或．
∴点表示的数是或．
故选：C．
7．A
解析：解：飞机无风时的航速为，风速为，
顺风的速度为：，
飞机顺风飞行的行程．
故选：A．
8．B
解析：解：由数轴上点的位置得：，，，
∴，，，，
故选：B．
9．D
解析：解：，
，
．
故选：D．
10．A
解析：解：∵每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等，
∴每个三角形各顶点上数字之和相等，如图1中，，则，
即：相邻两个三角形中非公共点的两个顶点数字之和相等，
∴在图2中，，解得：，
∴，
故选：A．
11．A
解析：解： ①整数和分数统称为有理数，故①正确；
②一个有理数可能不是正数也不是负数，比如0，故②错误；
③没有最小的正数，也没有最大的负数，故③错误；
④如果两个数的和是正数，那么这两个数中至少有一个正数，故④正确；
⑤，一定在原点的右边，故⑤错误．
其中正确的个数为2个．
故选A．
12．D
解析：解：∵第一个图形有个三角形，即有个三角形，
第二个图形有个三角形，即有个三角形，
第三个图形有个三角形，即有个三角形，
第四个图形有个三角形，即有个三角形，
∴第个图形有个三角形，
故选D．
13．
解析：海平面为基准，记为0米，
高于海平面100米的某地的高度记为米，
那么“奋斗者”号坐底深度10909米处，该处的高度可记为米，
故答案为：．
14．
解析：解：，
故答案为．
15．
解析：解：∵a、b互为相反数，c、d互为负倒数，n为最大的负整数，m是绝对值最小的有理数，
∴，，，，
∴原式
，
故答案为：
16．（n为正整数）
解析：解：已知式子可写成：，分母为奇数，可写成2n-1，分子中字母a的指数为偶数2n．
∴第n个式子是（n为正整数）．
故答案为：（n为正整数）．
17．
解析：解：
．
18．，2.
解析：解：
，
∵，
∴，
∴，
∴原式
．
19．(1)环卫驿站在岗亭南边，距离岗亭千米，数轴见解析．
(2)在清扫过程中，该车离开岗亭最远的距离是千米．
(3)上午共耗油升．
解析：（1）解：根据题意：
当天上午连续行驶，最终停留在环卫驿站，则
（千米）
规定向北方向为正，
环卫驿站在岗亭南边，距离岗亭千米，
如下图，数轴上标示出环卫驿站和岗亭的位置，
（2）第一次停下来与岗亭的距离为：
（千米）；
第二次停下来与岗亭的距离为：
（千米）；
第三次停下来与岗亭的距离为：
（千米）；
第四次停下来与岗亭的距离为：
（千米）；
第五次停下来与岗亭的距离为：
（千米）；
第六次停下来与岗亭的距离为：
（千米）；
第七次停下来与岗亭的距离为：
（千米）；
第八次停下来与岗亭的距离为：
（千米）；
即在清扫过程中，该车离开岗亭最远的距离是千米；
（3）根据题意，
当天上午连续行驶总距离为：
（千米），
上午共耗油：（升），
答：上午共耗油升．
20．(1)元；
(2)当吨时，所缴水费为元，当吨时，所缴水费为元，元，吨时，所缴水费为元．
(3)见解析．
解析：（1）解：该用户月份应缴水费是（元）；
（2）解：①吨时，所缴水费为元；
②吨时，所缴水费为元，元；
③吨时，所缴水费为元．
（3）解：同学们要积极行动起来，从我做起、从点滴做起，爱惜水、节约水、保护水．
21．（1）-3； （2）“A-C”的正确答案为-7x2-2x+2.
解析：（1）由题意得，, A+2B=(4+)+2-8， 4+=1，=-3，即系数为-3.
(2)A+C=,且A=，C=4，AC=
22．(1)甲旅行社收取组团两日游的总费用为元，若人数不超过人时，乙旅行社收取组团两日游的总费用为元，若人数超过人时，乙旅行社收取组团两日游的总费用为元；
(2)王老师应选择甲旅行社．
解析：（1）解：甲旅行社收取组团两日游的总费用为：元；
若人数不超过人时，乙旅行社收取组团两日游的总费用为：元，
若人数超过人时，乙旅行社收取组团两日游的总费用为：元；
（2）解：因为王老师组团参加两日游的人数共有人，所以甲旅行社收取组团两日游的总费用为：元，
乙旅行社收取组团两日游的总费用为元，
，
∴王老师应选择甲旅行社．
23．(1)
(2)①3，3，4；②，或1；③，7
解析：（1）解：由图的结果可知，，
故答案为：．
（2）解：①数轴上表示2和5的两点之间的距离是，
数轴上表示和的两点之间的距离是，
数轴上表示1和的两点之间的距离，
故答案为：3，3，4；
②数轴上表示和的两点和之间的距离是，
表示的是数轴上表示和的两点和之间的距离是2，且，，
或，
故答案为：，或1；
③式子表示的是数轴上表示的点到表示和5的两点的距离之和，
则当数轴上表示的点在表示和5的两点的中间（含两端点），即时，式子取最小值，最小值是，
故答案为：，7．月用水量
不超过6吨的部分
超过6吨但是不超过10吨的部分
超过10吨的部分
收费标准（元/吨）