



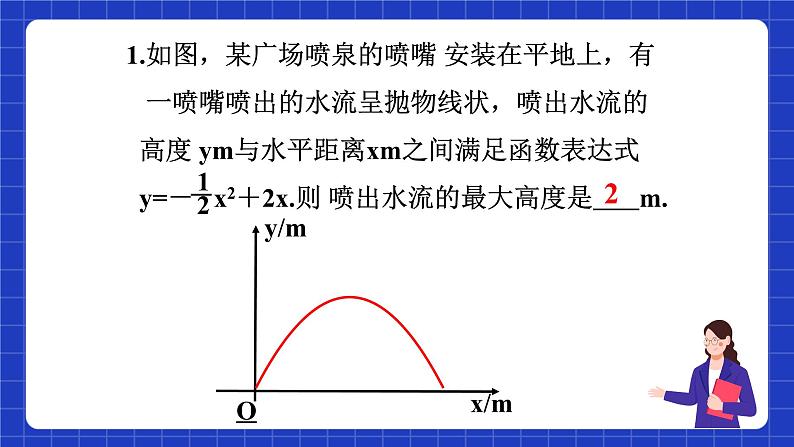


所属成套资源:沪科版数学九年级上学期PPT课件整套
初中数学沪科版(2024)九年级上册第21章 二次函数与反比例函数21.1 二次函数精品课件ppt
展开这是一份初中数学沪科版(2024)九年级上册第21章 二次函数与反比例函数21.1 二次函数精品课件ppt,共27页。PPT课件主要包含了课件说明,∵b4c1,∵a2>0,∴函数有最小值,∴最小值y,相应的x值为,复习旧知,-8-,∵a-4<0,∴函数有最大值等内容,欢迎下载使用。
二次函数是单变量最优化问题的数学模型,如生活中涉及的求最大利润,最大面积等.这体现了数学的实 用性,是理论与实践结合的集中体现.本节课主要来 研究利润问题.① y=2x2+4x+1, ② y =-4x2-8x-8
求出下列函数的最大值或最小值,并求出相应的x值.
∵ b=-8 ,c=-8,
① y=2x2-4x-1, ② y =-4x2-8x-8
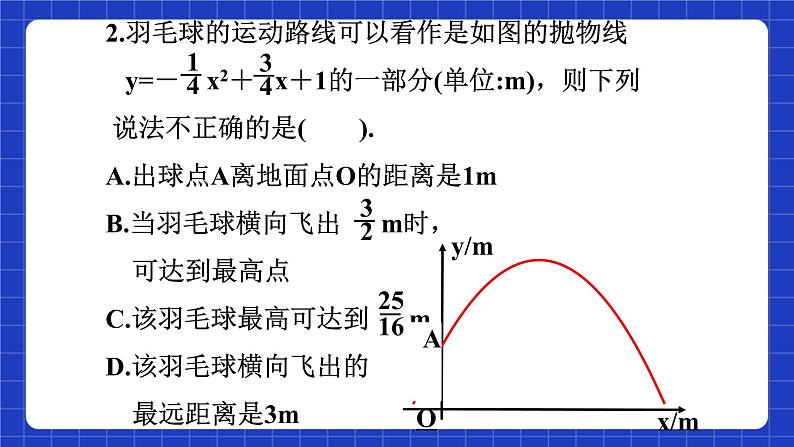
2.羽毛球的运动路线可以看作是如图的抛物线 y=- x2+ x+1的一部分(单位:m),则下列 说法不正确的是( ).A.出球点A离地面点O的距离是1mB.当羽毛球横向飞出 m时, 可达到最高点 C.该羽毛球最高可达到 mD.该羽毛球横向飞出的 最远距离是3m
3.从地面竖直向上抛出一小球,小球的高度 y m 与小球运动的时间x s之间的函数表达式为 y=ax2+bx+c(a≠0).若小球在第7s与第13s时的 高度 相同,则在下列时间中小球所在高度最高 的是( ). A.第8s B.第10s C. 第12 s D. 第 15 s
某商品现在的售价为每件 60 元,每星期可卖出300件.市场调查反映:如调整价格,每涨价 1 元,每星期要少卖出 10 件;每降价 1 元,每星期可多卖出 20 件.已知商品的进价为每件 40 元,如何定价才能使利润最大?
(1) 题目中有几种调整价格的方法?
(2) 题目涉及哪些变量?哪一个量是自变量?哪些量随之发生了变化?哪个量是函数?
题目中有2种调整价格的方法.
(3) 当每件涨 1 元时,售价是多少?
当每件涨 1 元时,售价是61元,
每星期销量是(300-10)=290件,
每件利润为 (61-40)=21元.
(4) 最多能涨多少钱呢?
(5) 当每件涨 x 元时,售价是多少?
当每件涨 x 元时,售价是(60+x)元,
每星期销量是(300-10x)件,
每件利润为 (60+x-40)元.
(300-10x)元
利润y=(60+x-40)
y=(20+x)(300-10x).
y=-10x2+100x+6000
(6)这是一个什么函数?
自变量取值范围是什么?
(300-10x)元.
某商品现在的售价为每件 60 元,每星期可卖出300件.市场调查反映:如调整价格,每涨价 1 元,每星期要少卖出 10 件,已知商品的进价为每件 40 元,如何定价才能使利润最大?
解:设每件涨 x 元时,利润为y元.
y=(60+x-40)(300-10x)
∴当定价 65 元 时,销售利润y 最大.
∵ a=-10<0 ,
(7) 当每件降 x 元时,售价是多少?
当每件降 x 元时,售价是(60-x)元,
每星期销量是(300+20x)件,
每件利润为 (60-x-40)元.
(300+20x)元
解:设每件降 x 元时,利润为y元.
y=-20x2+100x+6000
当定价 57.5 元 时,销售利润y 最大.
∵ a=-20<0 ,
∴当 时,
(300+20x)
即定价为57.5元时,
某商品现在的售价为每件 60 元,每星期可卖出300件.市场调查反映:每降价 1 元,每星期可多卖出 20 件.已知商品的进价为每件 40 元,如何定价才能使利润最大?
(7) 设降价后的定价为x 元,则降价降了多少元?
降价后的定价为x 元,降价降了(60-x)元,
每星期销量是[300+20(60 - x)]件,
每件利润为 (x-40)元.
多卖出20(60 - x)件;
[300+20(60 - x)]元
解:设定价为x元,利润为y元.
y=-20x2+2300x-60000
∴当定价 57.5 元 时,销售利润y最大.
[300+20(60-x)]
解决与价格或利润有关的最优化问题的方法 (1)由等量关系“总利润=每件利润×销售量”得到二次函数表达式; (2)将二次函数表达式配方、化成顶点式 (3)根据顶点式,结合x的取值范围,确定的函数的最值,从而确定最优方案.
y=a(x+h)2+k;
1.某商场降价销售一批衬衫,已知所获利润y元与 降价金额x元之间满足函数关系式y=-x2+20x +400,则所获利润最多为( ). A.10元 B.400元 C.500元 D.600元
2.某便民商店经营一种商品,在销售过程中, 发现一周利润y元与每件销售价x元之间的关 系满足y=-2(x-20)2+1558.已知销售价的范 围是15≤x≤22,则该便民商店一周可获得的 最大利润是( ). A.20元 B.1508元 C.1550元 D.1558
3.出售某种文具盒,若每个获利x元,则一天 可售 出(60-10x)个.设一天售出这种文具盒 获得的总利润为y元,那么y与x的函数表达式 是 . 当x= 时,一天售出这 种文具盒获得的总利润最大.
y=-10x2+60x
(1)这节课学习了用什么知识解决哪类问题? (2)解决问题的一般步骤是什么?应注意哪些问题? (3)你学到了哪些思考问题的方法?
1.某商店经营某种商品,已知每天获利y元与售价 x元/件之间满足关系式 y=-x2+80x-1000. 则当x= 时,每天获利最多,每天最多可获 利 元.
2.某公司在甲、乙两地同时销售某种品牌的汽车 已知在甲、乙两地的销售利润y万元与销售量x 辆之间分别满足:y1= -x2+10x,y2=2x.若该公 司在甲、乙两地共销售15辆该品牌的汽车,则 能获得的最大利润是( ). A.30万元 B.40万元 C.45万元 D.46万元
y=-x2+8x+30
3.某种商品每件进价为20元调查表明:在某段时间 内,若以每件x元(20≤x≤30,且x为整数)出售 可卖出(30-x)件.若要使利润最大,则每件商品 的售价应为 元.
=-x2+50x-600
相关课件
这是一份初中数学沪科版(2024)九年级上册<a href="/sx/tb_c44092_t3/?tag_id=26" target="_blank">22.1 比例线段优秀ppt课件</a>,共19页。PPT课件主要包含了学习新知,例题解析,练习巩固等内容,欢迎下载使用。
这是一份沪科版(2024)九年级上册<a href="/sx/tb_c44083_t3/?tag_id=26" target="_blank">第21章 二次函数与反比例函数21.1 二次函数试讲课课件ppt</a>,共34页。PPT课件主要包含了课件说明,最小值为,此时自变量x,复习旧知,最大值为,∴函数有最小值,相应的x值为,∴最小值y,∴函数有最大值,∴最大值y等内容,欢迎下载使用。
这是一份初中沪科版(2024)<a href="/sx/tb_c44083_t3/?tag_id=26" target="_blank">第21章 二次函数与反比例函数21.1 二次函数精品ppt课件</a>,共33页。PPT课件主要包含了∵a-4<0,∵b3c0,∴函数有最大值,∴最大值y,相应的x值为,∵b1c6,∴函数有最小值,∴最小值y,∵v010,g10等内容,欢迎下载使用。













