数学九年级上册第22章 相似形22.2 相似三角形的判定优秀课件ppt

这是一份数学九年级上册第22章 相似形22.2 相似三角形的判定优秀课件ppt，共27页。PPT课件主要包含了教学重点，教学难点，课件说明，相似多边形，学习新知，相似三角形，相似的表示方法，符号∽，读作相似于，相似比等内容，欢迎下载使用。
教学目标 1.了解相似多边形的概念，掌握相似三角形及其相似比的概念；能用符号正确表示两个三角形相似； 2.会运用平行线法证明三角形相似．
用平行线法证明三角形相似.
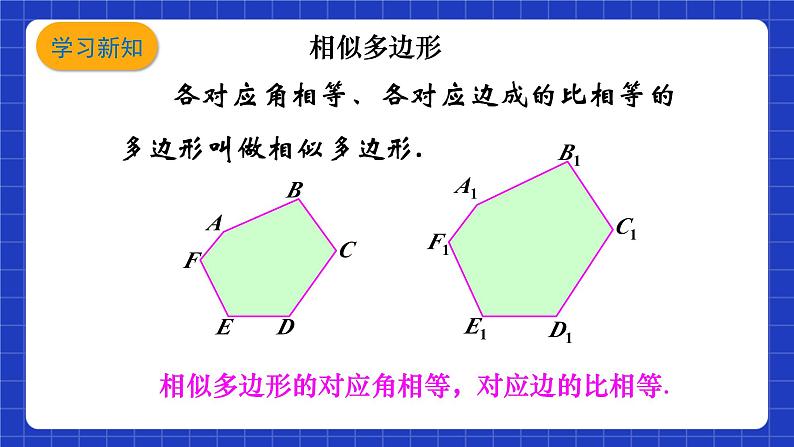
各对应角相等、各对应边成的比相等的多边形叫做相似多边形.
相似多边形的对应角相等，对应边的比相等.
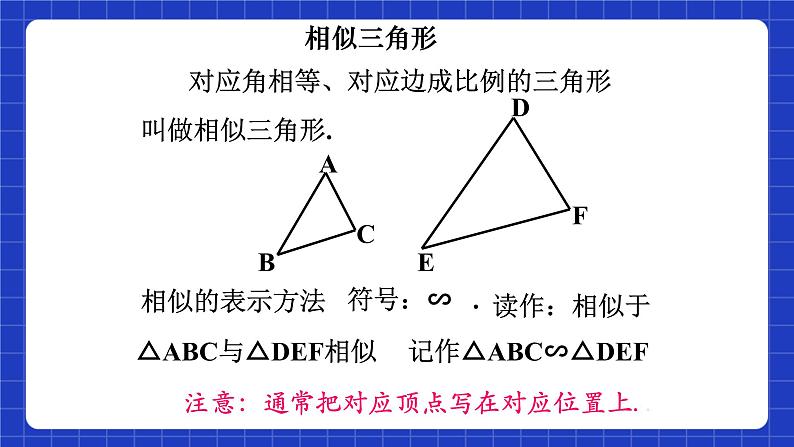
对应角相等、对应边成比例的三角形叫做相似三角形.
△ABC与△DEF相似
记作△ABC∽△DEF
注意：通常把对应顶点写在对应位置上. .
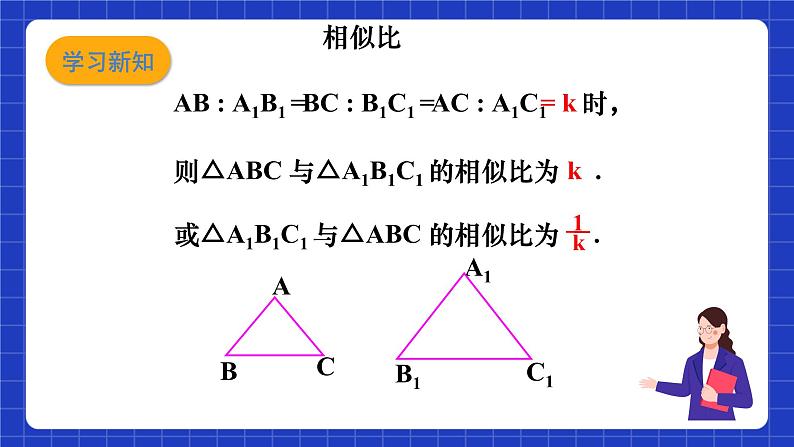
AB : A1B1 =
BC : B1C1 =
则△ABC 与△A1B1C1 的相似比为 k .或△A1B1C1 与△ABC 的相似比为 .
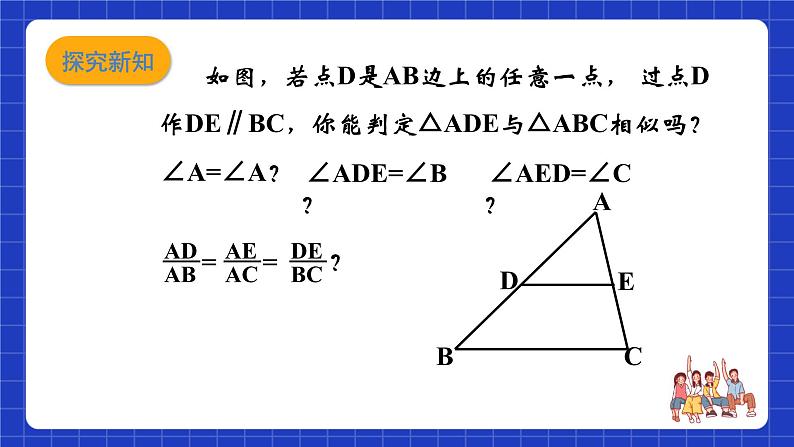
如图，若点D是AB边上的任意一点， 过点D作DE∥BC，你能判定△ADE与△ABC相似吗？
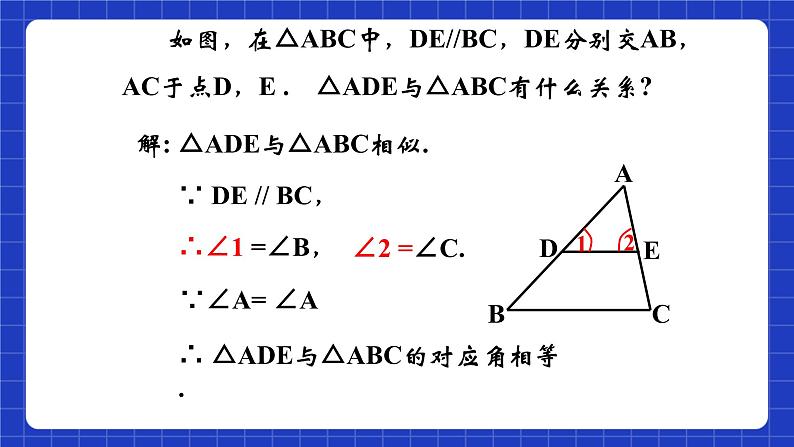
如图，在△ABC中，DE//BC，DE分别交AB，AC于点D，E . △ADE与△ABC有什么关系?
∵ DE // BC，
∴ △ADE与△ABC的对应角相等.
△ADE与△ABC相似.
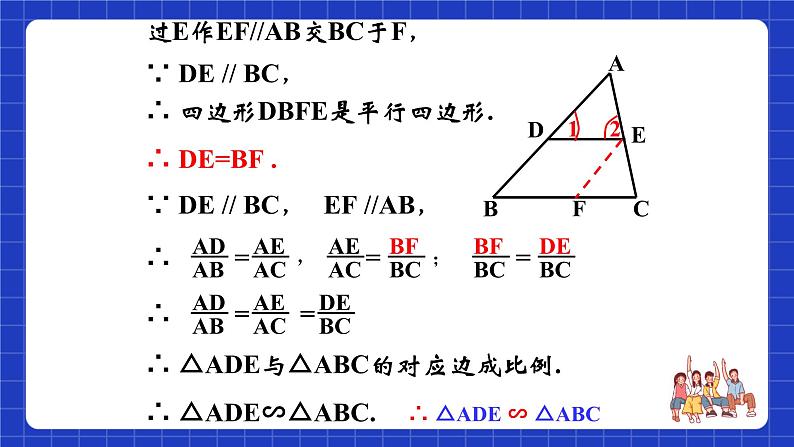
∴ 四边形DBFE是平行四边形.
∴ △ADE ∽ △ABC
过E作EF//AB交BC于F，
∴ △ADE与△ABC的对应边成比例.
∴ △ADE∽△ABC.
平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.
平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.定理可以适用以下三种情形：
∵DE∥BC∴△ADE∽△ ABC
如果再作 MN∥DE ，共有多少对相似三角形？
∴ ΔADE∽ΔDBF
∴ ΔDBF∽ΔABC
∴ ΔADE∽ΔABC
1.如图，在△ABC中，DE//BC，且AD=3，DB=2. 写出图中的相似三角形，并指出其相似比.
∴AB=AD＋DB=3＋2=5 ，
∴ △ADE与△ABC相似比为
图中共有____对相似三角形.
2. 已知：如图，AB∥EF ∥CD，
△AOB∽△FOE
3.如图，在△ABC中，DG∥EH∥FI∥BC，(1)请找出图中所有的相似三角形；(2)如果AD=1，DB=3，那么DG：BC=_____.
△ADG∽△AEH∽△AFI∽△ABC
∴DG：BC=AD：AB.
AB=AD＋DB=1＋3=4
∴ ΔADG∽ΔABC，
例2 如图，在△ABC中，DE∥BC，AD=EC，DB=1cm，AE=4cm，BC=5cm，求DE的长．
[解析] 要求线段DE的长 要求AC的长
AE：EC=AD：DB.
∴AE:EC=AD:DB.
∴AE:EC=EC:DB.
∴ EC2=DB · AE
∵ DB=1cm，AE=4cm，
∴DE:BC=AE:AC.
∴AC=AE＋EC=6cm.
∴DE= cm.
∴ ΔADE∽ΔABC.
4.如图，DE∥BC交AB于D，交AC于E，若AD：DB=2：3，BC=15，求DE的长.
∵AD：DB=2：3，
∴AD：AB=2：5.
5.如图，在□ABCD中，E是边BC上的一点，且 BE:EC=3:2，连接AE、BD交于点F，则 BE:AD=_____，BF:FD=_____.
∵BE:EC=3:2，
∴BE：BC=3：5.
∴BF：FD=BE：AD
∴BE：AD=3：5.
∵四边行ABCD是平行四边形
∴ △BEF∽△DAF
6.如图，在△ABC中，∠C的平分线交AB于D， 过点D作DE∥BC交AC于E，若AD:DB=3:2，则EC:BC=______.
∵AD:DB=3:2，
∴AD:AB=3:5.
∴EC:BC=AD:AB
∴ ΔADE∽ΔABC，
∴DE:BC=AD:AB，
3.用平行线法可证明哪类三角形相似？
1.相似三角形的定义怎样说？
2.相似三角形的相似比是指什么？
1.如图，在△ABC中，DE∥BC，AD=1，AB=4，则DE：BC=( ). A. 1:2 B. 1:3 C. 2:3 D. 1:4
2.如图，点F在□ ABCD的边AB上，射线CF交DA的延长线于点E在不添加辅助线的情况下，与△ AEF相似的三角形有( ). A. 0个 B. 1个 C. 2个 D. 3个
3.如图，在△ABC中，DE∥BC，AD：DB=3:2，则AE：EC= ，DE：BC= .
4.如图，AD∥EF∥BC，则图中的相似三角形共有 对，分别是 .
课本P72页第4、5、6题