初中数学沪科版（2024）九年级上册第22章 相似形22.3 相似三角形的性质公开课课件ppt

这是一份初中数学沪科版（2024）九年级上册第22章 相似形22.3 相似三角形的性质公开课课件ppt，共27页。PPT课件主要包含了教学重点，教学难点，课件说明，复习旧知，角平分线，探究新知，∴∠B∠B′，∠B∠B′，则ABkA′B′，ACkA′C′等内容，欢迎下载使用。
教学目标:掌握相似三角形对应的高，中线，角平 分线，周长，面积的比的性质．
用相似三角形对应的高，中线，角平 分线，周长，面积的比的性质解题.
用相似三角形面积的比的性质解题.
1.平行于三角形一边的直线与其他两边相交， 所构成的三角形与原三角形相似.
4.三边对应成比例的两个三角形相似.
3.两边对应成比例且夹角相等的两个三角形相似.
2.两角分别相等的两个三角形相似.
5.斜边和一条直角边应成比例的两个 直角三角形相似.
判断两个三角形相似的方法
(1)相似三角形有什么性质？
相似三角形对应角相等，对应边成比例.
(2)相似三角形的对应边的比叫什么？
(3)△ABC和△A′B′C′的相似比为k， 则△A′B′C′和△ABC的相似比是多少？
相似三角形的对应边的比叫相似比.
△A′B′C′和△ABC的相似比是 .
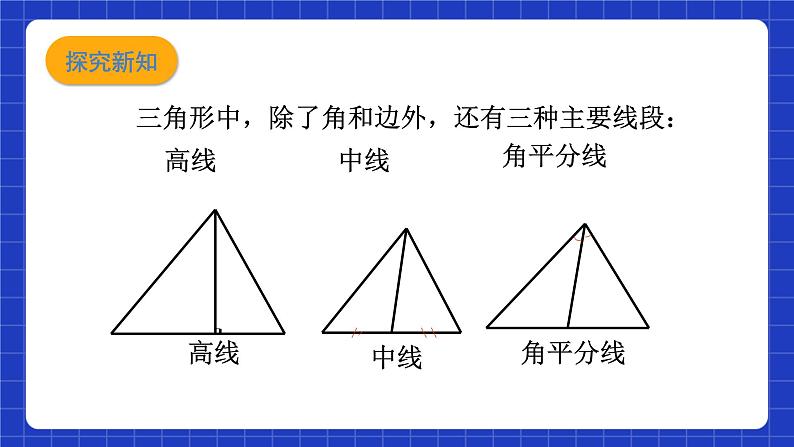
三角形中，除了角和边外，还有三种主要线段：
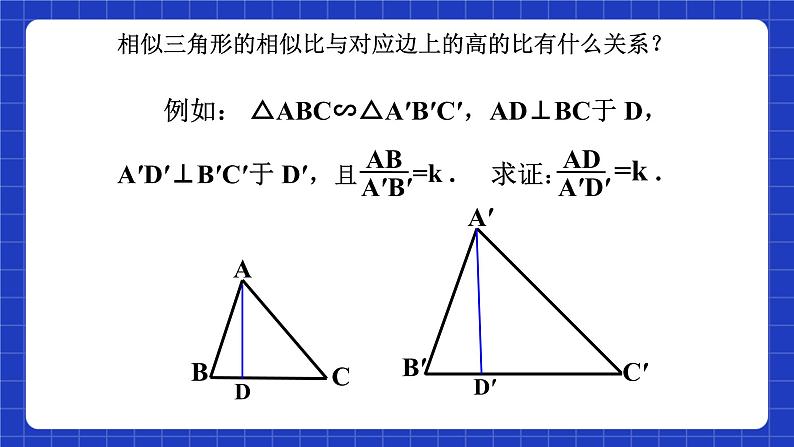
相似三角形的相似比与对应边上的高的比有什么关系？
例如： △ABC∽△A′B′C′，AD⊥BC于 D， A′D′⊥B′C′于 D′，且 求证：
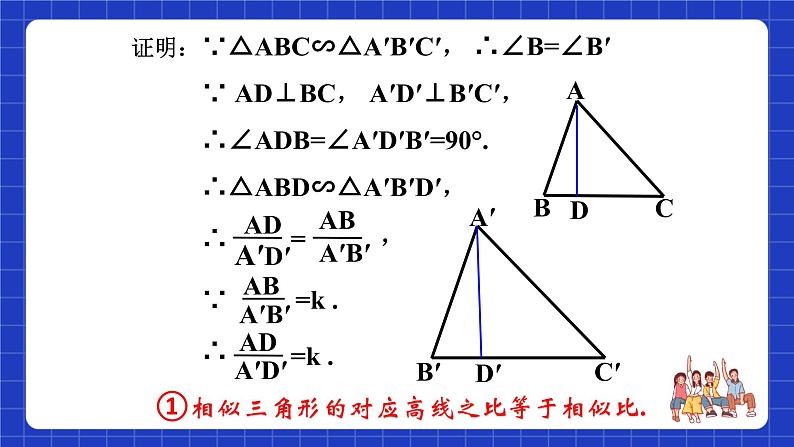
①相似三角形的对应高线之比等于相似比.
∵ AD⊥BC， A′D′⊥B′C′，
∴∠ADB=∠A′D′B′=90°.
∴△ABD∽△A′B′D′，
∵△ABC∽△A′B′C′，
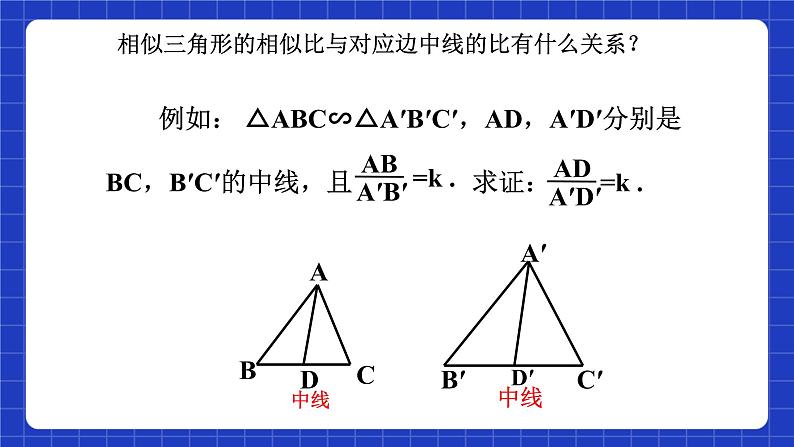
相似三角形的相似比与对应边中线的比有什么关系？
例如： △ABC∽△A′B′C′，AD，A′D′分别是BC，B′C′的中线，且 求证：
②相似三角形对应 边中线之比等于相似比.
证明:∵△ABC∽△A′B′C′，
∴
∵AD、A′D′是中线，
∴ △ABD∽△A′B′D′，
∴BD= BC ，
∴
B′D′= B′C′.
相似三角形的相似比与对应角平分线的比有什么关系？
例如： △ABC∽△A′B′C′，AD平分∠BAC，A′D′平分∠B′A′C′，且 求证：
相似三角形的对应角平分线之比等于相似比.
∴∠BAC=∠B′A′C′，
∵AD、A′D′是角平分线，
∴∠BAD= ∠BAC ，
∴∠BAD =∠B′A′D.
∠B′A′D′= ∠B′A′C′.
如果两个三角形相似，它们的周长之间有什么关系？
相似三角形周长的比等于相似比.
A′B′ ＋B′C′ ＋A′C′
k(A′B′ ＋B′C′ ＋A′C′)
如图，△ABC∽△A′B′C′，相似比为k，它们的面积比是多少？
相似三角形面积的比等于相似比的平方.
(1)相似三角形对应的 高、中线、角平分线 的比等于相似比.
(3)相似三角形面积的比等于相似比的平方.
(2)相似三角形周长的比等于相似比.
相似三角形的相似比等于面积比的算术平方根.
1.已知：△ABC∽△A′B′C′，BC=3.6cm， B′C′=6cm，AE是△ABC的一条中线，AE=2.4cm， 求△A′B′C′中对应中线A′E′的长.
∴A′E′:AE= B′C′:BC
∵BC=3.6cm，B′C′=6cm，AE=2.4cm，
∴A′E′:2.4= 6:3.6
∴A′E′=4(cm).
1.已知 △ABC∽△A′B′C′，的相似比为2：3，则周长比为 ，对应边上中线之比 ，面积之比为 .
(2)已知△ABC∽△A′B′C′，且面积之比为9：4，则相似比为 ，对应边上的高之比为 ，周长之比为 ，.
3.如图，在△ABC中，D是AB的中点， DE∥BC则:
(1)S△ADE : S △ABC = ；
(2)S△ADE: S 梯形DBCE = .
(1)一个三角形对应的各边长扩大为原来的5倍，这个三角形的角平分线也扩大为原来的5倍. ( )
4.判断题 (正确的画“ ”，错误的画“ ”).
(2)一个三角形对应的各边长扩大为原来的9倍，这个三角形的面积也扩大为原来的9倍. ( )
5.在一张复印出来的纸上，一个三角形的一条边由原图中的2cm变成了6cm，放缩比例是多少？这个三角形的面积发生了怎样的变化？
答：放缩比例是1:3；
这个三角形的面积扩大为
数学花絮和哥们儿去吃披萨，点了个12寸的.过了会儿，服务员来了说：“不好意思，现在做不了12寸了，您看换成两个6寸的可以吗，一样的.” 哥们听了，微微一笑：“能一样吗？ ”
1.这节课我们学习了相似三角形对哪些性质？
2.我们利用相似三角形性质解决问题时要注意的 关键问题是什么？
在△ABC中，BC=15cm，CA=45cm， AB=63cm，另一个和它相似的三角形的最短边是5cm，则最长边是( ). A.18cm B.21cm C.24cm
2. 等腰△ABC和△DEF相似，其相似比为3：4， 则它们底边上对应高线的比为( ). A．3：4 B．4：3 C．1：2 D．2：1
3.两个三角形周长之比为9：5，则面积比为( ). A.9∶5 B.81∶25 C.3∶ D.不能确定
4.两个相似三角形的相似比为2∶3，它们周长 的差是25，那么较大三角形的周长是____， 这两个三角形的面积比为 .
课本P90页第1、2题